05 dominio e segno di razionali fratte ed esponenti

Esempio 13 (razionali fratte p308n44-45)
Studiare dominio e segno della seguente funzione:
y=
2x 2 − 7x + 3
x 2 − 3x + 2
Studio del Dominio
Una funzione razionale fratta è definita solo per valori
della x che non annullano il denominatore:
x 2 − 3x + 2 ≠ 0
⇒
x ≠ 1∧x ≠ 2
0
1
2
1
3
2
D : ℝ − {1;2} I
⇒
n corrispondenza di questi valori tracceremo linee
verticali se essi non annullano anche il numeratore, come
in questo caso.
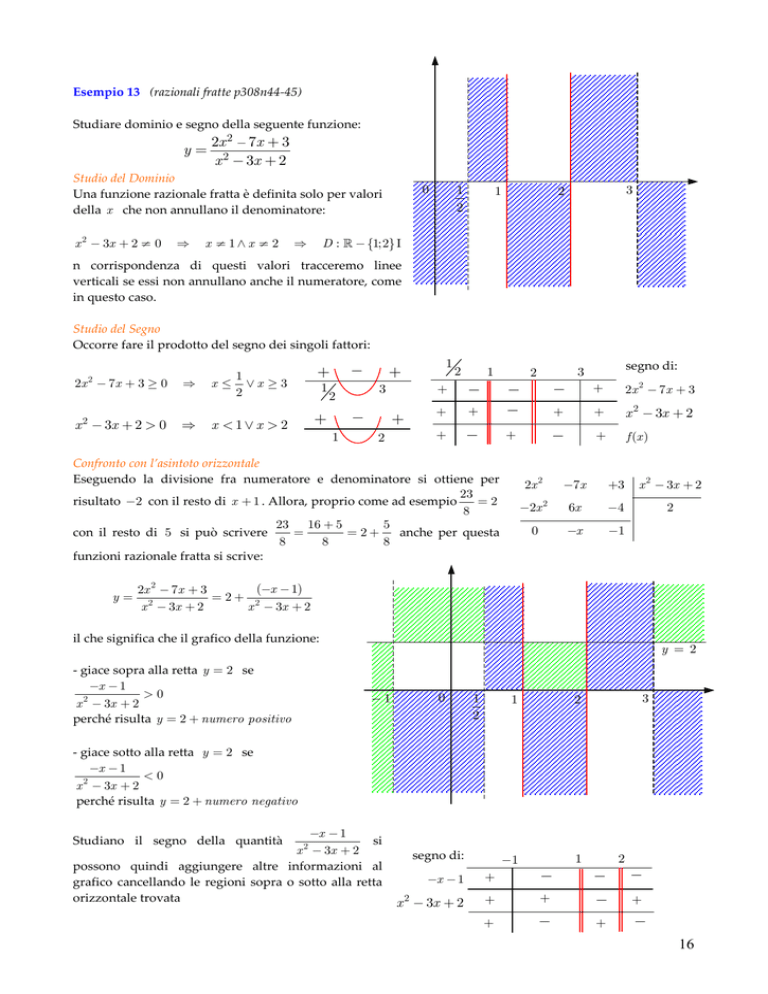
Studio del Segno
Occorre fare il prodotto del segno dei singoli fattori:
2
2x − 7x + 3 ≥ 0
x 2 − 3x + 2 > 0
⇒
⇒
1
x ≤ ∨x ≥ 3
2
x <1∨x > 2
−
+
1
3
2
−
+
1
1
+
+
2
2
1
−
+
2x 2 − 7x + 3
+
−
−
+
+
x 2 − 3x + 2
−
+
−
+
f (x )
+
−
+
+
Confronto con l’asintoto orizzontale
Eseguendo la divisione fra numeratore e denominatore si ottiene per
23
=2
risultato −2 con il resto di x + 1 . Allora, proprio come ad esempio
8
23 16 + 5
5
con il resto di 5 si può scrivere
=
=2+
anche per questa
8
8
8
funzioni razionale fratta si scrive:
y=
segno di:
3
2
2x 2
−7x
+3
x 2 − 3x + 2
−2x 2
6x
−4
2
0
−x
−1
(−x − 1)
2x 2 − 7x + 3
=2+ 2
2
x − 3x + 2
x − 3x + 2
il che significa che il grafico della funzione:
- giace sopra alla retta y = 2 se
−x − 1
>0
x 2 − 3x + 2
perché risulta y = 2 + numero positivo
y = 2
−1
0
1
2
1
2
−1
1
3
- giace sotto alla retta y = 2 se
−x − 1
<0
2
x − 3x + 2
perché risulta y = 2 + numero negativo
−x − 1
si
x 2 − 3x + 2
possono quindi aggiungere altre informazioni al
grafico cancellando le regioni sopra o sotto alla retta
orizzontale trovata
Studiano il segno della quantità
segno di:
2
−x − 1
+
−
−
−
x 2 − 3x + 2
+
+
−
+
+
−
+
−
16
Esempio 14 (Esponenti reali ReF p. 309 da 60 a 63)
Studiare dominio e segno della seguente funzione:
2

3
9
7
y = x 3 + x 2 + x − 3


2
2
−2
−3
1
0
2
Studio del Dominio
Una potenza ad esponente razionale (non intero) oppure
irrazionale, accetta solo valori positivi o nulli come base.
La condizione di esistenza è pertanto:
x3 +
9 2 7
x + x −3 ≥ 0
2
2

2
9
7
Si faccia attenzione che applicando le proprietà degli esponenti ottiene y = 3 x 3 + x 2 + x − 3 , il cui


2
2
dominio è ℝ . Ma le proprietà degli esponenti valgono solo se la base è positiva, il che riconduce alla
condizione di esistenza già scritta. Cerchiamo le radici dell’equazione associata:
9 2 7
x + x −3 = 0
2
2
3
2
2x + 9x + 7x − 6 = 0
x3 +
trasformata in un’equazione a coefficienti interi possiamo individuare dei candidati ad essere
razionali. Essendo i divisori del termine noto 6, 3, 2,1 mentre 2,1 sono i divisori del termine
3
1
massimo, le radici razionali sono da ricercare fra i numeri ±6, ±3, ±2, ± , ±1, ± . Proviamo
2
2
1
1
x = . Come si vede x =
è radice. Val la pena di
2
2
7 −6
2
9
2
9
ricordare che la regola di Ruffini, applicata ad un
1
1
2
11
18
numero che non è radice, produce il valore del
2
1
2 11 18 12
polinomio nel punto che abbiamo utilizzato.
2 10
Scomponiamo:
⇒
+
x ≥ 12
2x 2 + 10x + 12 ≥ 0
⇒
x = 1 ed
7
−6
5
6
12
0
valore del
polinomio in x=1
(x − 1 2)(2x 2 + 10x + 12) = 0
x − 12 ≥ 0
soluzioni
di grado
−3
−
+
−2
x ≤ −3 ∨ x ≥ −2
segno di:
x −1
2
2x 2 + 10x + 12
−3
1
−2
2
−
−
−
+
+
−
+
+
−
+
−
+
quindi D : [−3; −2] ∪ [ 1 2 ; +∞)
Studio del Segno
Una potenza con esponente reale, a base quindi necessariamente positiva, dove esiste è sempre positiva
quindi risulta f (x ) ≥ 0 ∀x ∈ D .
17