1 Ex ∈ E - francescopoli.net

ℝ
1. Sottoinsiemi dei numeri reali
d s
i
Studieremo le proprietà dei sottoinsiemi dei numeri reali,
E ⊆ ℝ , che hanno a e emp o la forma:
−3
3
2
5
E = (−3,2) ∪ (3, 5)
2
1
5
8
6
E = [1,2] ∪ {5; 6; 8}
−1
1
2
3
2
E = (−∞, −1) ∪
4
{12 } ∪ (2, 3) ∪ [4, +∞)
i
allora diremo
Definizione: Sia E un sottoinsieme di
ℝ , c oè E ⊆ ℝ ,
maggiorante di E un qualunque numero M
tale che
t
r
l
∀x ∈ E isu i x ≤ M .
it
i
Eè
t iE i
Definizione: Se es s e almeno un magg oran e d d remo che
limitato superiormente
x ∈E
M
i E un qualunqu num ro m tal
e
e
e
Definizione: Sia E un sottoinsieme di ℝ , cioè E ⊆ ℝ , allora diremo minorante d
che ∀x ∈ E risulti x ≥ m .
it
i
t i E ir o ch E è
limitato inferiormente
d em e
Definizione: Se es s e almeno un m noran e d
x∈E
m
ia E un sottoinsieme di
i
allora diremo e E è
ia limitato
ℝ , c oè E ⊆ ℝ ,
ch
limitato se è s
f
io
m
t
limitato
i
io
m
t
n er r en e.
super r en e che
Definizione: S
E
ia E un sottoinsieme di
iù icc dei magg ioranti di E o chiameremo
di E se
l
Definizione: S
ℝ . Il p p olo
massimo
a artiene ad E a trimenti o chiameremo
di E
estremo superiore
pp
l
l
1
E
Massimo
E
Estremo superiore
E
minimo
E
Estremo inferiore
Esempio 1
Trovare gli estremi inf eriore e superiore degli insiemi:
E1 = {−2;1;2} ∪ (3; 6) , E2 = (−4; 3) ∪ (5;7] ,
ttono massimo o minimo.
e
dire
se
amme
E = (−∞; 3] ∪ (5; +∞)
3
L’insieme dei minoranti di E1 è (−∞; −2] , l’insieme dei maggioranti [6; +∞) quindi:
min (E1 ) = −2 ,
sup (E1 ) = 6 , non ammette massimo
l’insieme dei minoranti di E2 è (−∞; −4] , l’insieme dei maggioranti [7; +∞) quindi:
inf (E1 ) = −4 , non ammette minimo
max (E2 ) = 7
mentre E 3 è illimitato.
Esempio 2
Trovare gli estremi inf eriore e superiore dell’insieme
tt
E = { x − 3 < 2} e dire se amme e massimo o minimo.
Riscriviamo la condizione data risolvendo la disequazione:
−2 < x − 3 < 2
1<x <5
risulta quindi inf(E ) = 1 , sup(E ) = 5 . L’insieme non ammette né massimo né minimo.
Esempio 3
Trovare gli estremi inf eriore e superiore dell’insieme
Vediamo qualche elemento: E =
{
E= x=
n −1
,n ∈ ℕ 0
n
} e dire se ammette massimo o minimo.
{12 , 23 , 43 ,…} . Riscriviamo la condizione:
n −1 n 1
1
= − = 1−
n
n n
n
2
1
è sempre positiva e minore di 1, e la x diviene sempre più grande al
n
crescere di n , tendendo ad 1 senza raggiungerlo mai. Quindi si ha sup(E ) = 1 , e non ammette massimo,
essendo n intero positivo la quantità
mentre se n = 1 l’insieme assume il suo valore più piccolo, min(E ) = 0 .
Esempio 4
{
Trovare gli estremi inferiore e superiore dell’insieme E = x =
{
}
2n + 1
, n ∈ ℕ 0 e dire se ammette massimo o minimo.
3n
}
5 7
Vediamo qualche elemento: E = 1, , , … . Riscriviamo la condizione:
6 9
2n + 1 2n
1
2
1
x=
=
+
= +
3n
3n 3n
3 3n
1
1
Essendo n > 0 , risulta sempre
< , quindi
3n
3
2 1
x ≤ + =1
3 3
valore che viene assunto per n = 1 cui max(E ) = 1 . Viceversa i numeri dell’insieme si ottengono sommando
2
1
2
a la quantità positiva
, che diventa arbitrariamente piccola al crescere di n . Si ha dunque x > ,
3
3n
3
2
valore che non viene mai assunto e quindi inf(E ) = .
3
Studiare ReF p. 10-12; es. p. 305 n. 1,3,4
Altri esercizi:




n2 + 1
1
5n + 2
n
E = x =
, n ∈ ℕ 0  , E = x = 2 , n ∈ ℕ 0 , E = x =
,n ∈ ℕ 0 , E = 
, n ∈ ℕ 0 
x =



n
4n
n +1
n





{
}
{
}
3
2. Intorno e punto di accumulazione
Definizione: siano a ∈ ℝ e b ∈ ℝ . Diremo intervallo aperto il sottoinsieme ] a, b [ di ℝ tale che a < x < b
a
b
Definizione: siano a ∈ ℝ e b ∈ ℝ . Diremo intervallo chiuso il sottoinsieme [ a, b ] di ℝ tale che a ≤ x ≤ b
a
b
Definizione: sia x 0 ∈ ℝ . Diremo intorno di x 0 , I (x 0 ) ogni intervallo aperto contente x0 .
Se δ1 ∈ ℝ +0 e δ2 ∈ ℝ +0 avremo pertanto: I (x 0 ) = ] x 0 − δ1 , x 0 + δ2 [
x 0 − δ1
x 0 + δ2
x0
ico
Inoltre se δ1 = δ2 ≡ δ l’intorno si dirà sfer
tr
o anche simme ico: I (x 0 ) = x ∈ R :
x0 − δ
x0
{
| x − x 0 |< δ
}
x0 + δ
Si definiscono anche l’ intorno destro: I (x 0 ) = ] x 0 , x 0 + δ [ ; l’ intorno sinistro I (x 0 ) = ] x 0 − δ, x 0 [ .
Definizione: diciamo intorno di +∞ un qualunque insieme della forma (a, +∞) , intorno di −∞
qualunque insieme della forma (−∞, b) , intorno di ∞ qualunque insieme tipo (−∞, a ) ∪ (b, +∞) .
Definizione: Sia E un sottoinsieme di ℝ . Si dice che x0 è punto di accumulazione per E se in ogni intorno di x0
cade almeno un elemento di E diverso da x0 .
E
sono punti di accumulazione
non è punto di accumulazione
Si noti che i punti di frontiera di un intervallo sono punti di accumulazione per esso, pertanto diremo anche
che un intervallo è chiuso se contiene tutti i suoi punti di accumulazione.
Notare:
1) se cade almeno un punto di E in un intorno di un punto di accumulazione allora ce ne cadono
infiniti
2) non è detto che il punto di accumulazione appartenga ad E. esempi ne sono tutti gli intervalli aperti,
l’insieme dei reali pari ai naturali
1
con n ∈ ℕ 0 dove zero è un punto di accumulazione ma non
n
lo è nessun numero dell’ insieme.
3) Se esiste almeno un intorno del punto che non contiene altri elementi di E il punto si dice isolato
4
Esempio 6
{
Trovare i punti di accumulazione dell’insieme E = x = 5 +
}
1
; n ∈ ℕ 0 , l’estremo superiore e quello inferiore e dire
n
se ammette massimo e minimo.
Si tratta di un insieme dove tutti gli elementi sono numeri razionali.
n =1⇒ x =6
11
n =2⇒x =
2
16
n =3⇒x =
3
21
n =4⇒x =
4
26
n =5⇒x =
5
…
Comunque si scelgano due elementi di E, nell’ intervallo fra di loro non sono compresi altri elementi
dell’insieme quindi si può trovare sempre per ogni punto un intorno che non contiene altri punti di E. Ne
concludiamo che nessun elemento dell’insieme è punto di accumulazione. Invece è punto di accumulazione
x = 5 perché qualunque δ si scelga come raggio dell’intervallo di centro 5 esiste sempre un valore di n
1
abbastanza grande per cui risulti < δ .
n
5 26
5
21
4
16
3
11
2
6
Per lo stesso motivo si ha che inf(E ) = 5 , l’insieme non ammette minimo, ed inoltre max(E ) = 6 .
(Re Fraschini pp.12-14, es. P. 305 n.8, 9,13)
5
1. Definiz ione di funz ione
Una coppia ordinata di oggetti è un insieme costituito da due oggetti {a; b} individuato oltre che dagli
oggetti in questione dalla loro disposizione ordinata, vale a dire che {a; b} è differente da {b; a}. Ad esempio
sono coppie ordinate {1; 4} , {3.11; a} ,{Mario; Alberto} e così via.
Con il termine funzione si intende un insieme di coppie ordinate di oggetti e precisamente:
Definizione: Si definisce funzione f un insieme di coppie ordinate di oggetti (x; y) in cui non ve ne siano mai
due con lo stesso primo membro
L’insieme di tutti i valori x che compaiono al primo membro delle coppie ordinate (x; y) di una funzione f è
detto dominio di f, mentre l’insieme di tutti i valori che compaiono a secondo membro di tali coppie è detto
codominio di f. Per una funzione ad ogni valore di x nel dominio corrisponde quindi un solo valore di y nel
codominio e quindi si scrive solitamente:
f :D→C
dove con D si è indicato il dominio di f e con C il suo codominio. Alla grandezza x si dà il nome di variabile
indipendente mentre alla y quello di variabile dipendente. Il motivo di tale denominazione è che è comodo
pensare alla funzione come ad una sorta di legge che, noto un valore della x, fornisce un modo per trovare
un valore della y corrispondente ad esso. In questo senso una seconda possibile definizione di funzione è
Definizione: Dati due insiemi A e B si dice funzione di A in B una legge che associ ad ogni elemento di A uno ed un
solo elemento di B f : A → B
Questa seconda definizione, che è quella più largamente adottata nei testi scolastici, ci soddisfa un po’ meno
poiché il termine legge di cui essa fa uso è in qualche modo sinonimo di funzione, e quindi in realtà non
definisce molto, si limita a fare appello all’intuizione, assumendo il concetto di funzione come primitivo.
Quindi, per non cadere in definizioni circolari, penseremo ad una funzione come semplicemente ad una
tabella di valori, oppure se si tratta di una funzione di variabile reale che produce numeri reali, al suo
grafico. Il codominio C della funzione è in questo caso l’insieme degli elementi di B che sono immagine di
almeno un elemento di A, cioè C ⊆ B .
Come si è detto le coppie (x; y) possono essere qualsiasi cosa, ma noi ci limiteremo allo studio delle funzioni
in cui x ed y sono dei numeri reali. Chiameremo l’oggetto del nostro studio funzioni reali di variabile reale:
dire funzione reale significa dire che y ∈ ℝ mentre dire variabile reale significa che x ∈ ℝ . L’insieme delle
coppie ordinate che costituiscono una funzione reale di variabile reale può essere rappresentato sul piano
cartesiano dando luogo a quello che viene detto il grafico della funzione. Assegnare una funzione dando
l’insieme di tutte le coppie che la costituiscono non è fattibile poiché trattandosi di numeri reali in generale
avremo a che fare con un’infinità di coppie. Molte delle funzioni reali di variabile reale possono però essere
espresse in modo sintetico attraverso una relazione fra il numero reale x ed il numero reale y, relazione di
natura geometrica, od anche algebrica. Si pensi alle funzioni che già conosciamo: la funzione seno, ad
esempio, associa attraverso un procedimento geometrico ad un numero reale x, che rappresenta in questo
caso la misura della lunghezza di un arco, un numero reale y pari alla misura dell’ordinata del punto
individuato da quell’arco sul cerchio goniometrico. Noto il procedimento non è necessario specificare le
infinite coppie di valori ma più sinteticamente scriviamo y = sin x . Ogni volta che associamo ad una
funzione una scrittura sintetica sotto forma di equazione, del tipo:
y = f (x )
6
stiamo in realtà intendendo sinteticamente una serie di istruzioni che a partire da un valore della x ci
consentano di ricavare un valore della y. Si tratta soprattutto di procedimenti di natura geometrica: x ed y
sono misure di lunghezze legate da qualche specifico procedimento. In questo modo risulta costituito una
sorta di alfabeto delle funzioni, dette funzioni elementari:
1.
2.
le potenze intere: y = x ; y = x 2 ; y = x 3 etc
la funzione valore assoluto: y =| x |
3.
4.
5.
6.
le radici ennesime: y = x ; y = 3 x etc
le funzioni goniometriche: y = sin x ; y = cos x ; y = tan x ; y = cotan x
le funzioni goniometriche inverse: y = arcsin x ; y = arccos x ; y = arctan x
le funzioni esponenziali e logaritmiche: y = loga x ; y = a x
Attraverso di esse possiamo ottenere una grande varietà di funzioni reali di variabile reale: si tratta
semplicemente di combinarle tramite le operazioni algebriche o facendo agire le funzioni elementari
successivamente. Chiaramente questo procedimento non esaurisce tutte le funzioni reali di variabile reale,
anzi vi sono alcune funzioni delle quali è espressamente noto che non possono essere espresse tramite una
equazione che coinvolga combinazioni di funzioni elementari; però costituisce una piattaforma dalla quale
partire. Da ultimo si faccia attenzione al fatto che una funzione associa a ciascuno degli elementi del
dominio un solo elemento dell’insieme di arrivo. Osservando l’esempio a destra si vede che c’è un punto
nell’insieme di partenza associato a due punti nell’insieme di arrivo, e quindi non si tratta di una funzione.
è una funzione
non è una funzione
Per un motivo analogo non sono funzioni i grafici completi di circonferenze, ellissi ed iperboli (eccetto le
funzioni omografiche), né lo sono i grafici di parabole con asse orizzontale. Possono però esserlo delle loro
porzioni
f (a)?
f (a)?
a
a
x 2 + y2 = 1
non è una funzione
y2 = x
y = 1−x2
è una funzione
y= x
non è una funzione
è una funzione
7
2. Studio del dominio e del segno delle funz ioni
Si è soliti iniziare lo studio delle funzioni con il dominio. I casi da escludere sono solo i seguenti:
1.
n
2.
g(x )
⇒ f (x ) ≠ 0
f (x )
3.
loga f (x ) ⇒ f (x ) > 0
4.
α
g (x )
[ f (x )] , α ∈ ℝ ⇒ f (x ) ≥ 0; [ f (x )] ⇒ f (x ) > 0
f (x ), n pari ⇒ f (x ) ≥ 0
π
+ k π; k ∈ ℤ
2
arcsin f (x ), arcsin f (x ) ⇒ −1 ≤ f (x ) ≤ 1
tan f (x ) ⇒ f (x ) ≠
5.
6.
A seguire si procede con lo studio del segno, cioè con la ricerca dell’insieme di positività e di negatività.
Esempio 7
(analoghi ReF p312-313da114a120)
Studiare dominio e segno della seguente funzione:
y = x 3 − 7x + 6
Studio del Dominio
La funzione è un polinomio di terzo grado. Poiché non è presente nessuno dei casi di esclusione elencati
sopra il dominio è tutto l’insieme dei numeri reali
D:ℝ
Studio del Segno
Scomponiamo il polinomio in fattori. Com’è noto le radici razionali di un polinomio a coefficienti interi, se
esistono, sono da ricercare della forma:
±
divisori del termine noto
divisori coefficiente grado max
abbiamo che i divisori del termine noto 6 sono 6, 3,2,1 , mentre il coefficiente del termine di grado massimo
è 1 . Sono quindi candidati ad essere radici razionali i numeri ±6, ±3, ±2, ±1 .
3
Verifichiamo x = 3 :
3 − 7 × 3 + 6 = 12 che non è radice.
Verifichiamo x = −3 − 27 + 21 + 6 = 0 che è radice.
Eseguiamo quindi la divisione del polinomio per x + 3 oppure adoperiamo Ruffini:
x3
−x 3
0
−3x 2
0
−3x 2
3x 2
0
−7x
0
−7x
6
0
9x
2x
6
0
6
−2x
0
−6
0
x +3
x − 3x + 2
2
1
−3
1
0 −7 6
−3 9 −6
−3 2
0
−
+
1
+
2
8
Le altre due radici, 1 e 2 si trovano facilmente risolvendo
l’equazione x 2 − 3x + 2 = 0 . Riscrivendo la funzione nella
forma f (x ) = (x + 3)(x 2 − 3x + 2) eseguiamo il prodotto dei
segni:
−3
1
2
segno di x − 3x + 2 +
+
−
+
−
+
+
+
−
+
−
+
2
segno di x + 3
−3
0
1
2
Nel piano cartesiano si procede quindi a cancellare le
regioni dove la funzione non esiste.
Esempio 8
Studiare dominio e segno della seguente funzione:
y = x 3 − 7x + 6
Studio del Dominio
La funzione è una radice di indice pari di polinomio di terzo grado. Questa è definita solo per valori positivi
o nulli dell’argomento. Dobbiamo imporre quindi:
x 3 − 7x + 6 ≥ 0
Avendo già studiato il segno di questo polinomio
nell’esempio precedente possiamo concludere che:
D : [−3;1] ∪ [2; +∞)
−3
Nel piano cartesiano si procede quindi a cancellare le regioni
dove la funzione non esiste.
0
1
2
Studio del Segno
Una radice di indice pari, laddove esiste, è sempre positiva o
nulla. Possiamo quindi concludere che:
x 3 − 7x + 6 ≥ 0
∀x ∈ D
e quindi cancellare il semipiano negativo nelle regioni rimaste.
Esempio 9
Studiare dominio e segno della seguente funzione:
y = 4 − x2
Studio del Dominio
La funzione è una radice di indice pari di polinomio di secondo grado.
9
Dobbiamo imporre quindi:
−2
4 − x2 ≥ 0
−
2
−
+
che risolta fornisce :
D : [−2;2]
0
−2
2
Studio del Segno
Una radice di indice pari, laddove esiste, è sempre positiva o
nulla. Possiamo quindi concludere che:
4 − x2 ≥ 0
∀x ∈ D
e quindi cancellare il semipiano negativo nelle regioni
rimaste
Esempio 10
Studiare dominio e segno della seguente funzione:
y=
x −3
x 2 + 2x
Studio del Dominio
La funzione è una radice di indice pari di una funzione razionale fratta. Questa è definita solo per valori
positivi o nulli dell’argomento. In aggiunta dobbiamo escludere quei valori che rendono nullo il
denominatore. Dobbiamo imporre quindi:
 x − 3
 2
≥0
 x + 2x


 2
x + 2x ≠ 0
Studiamo il segno della prima quantità facendo il prodotto dei suoi fattori:
x 2 + 2x ≥ 0 ⇒ x (x + 2) ≥ 0 ⇒ (−∞; −2] ∪ [0; +∞)
−
+
x −3 > 0 ⇒ x > 3
−2
−2
0
+
0
3
segno di x − 3
−
−
−
+
segno di x 2 + 2x
+
−
+
+
−
+
−
+
possiamo concludere che D : (−2; 0) ∪ [3; +∞)
Studio del Segno
Una radice di indice pari, laddove esiste, è sempre positiva o nulla. Possiamo quindi concludere che:
10
x −3
≥0
x 2 + 2x
∀x ∈ D
e quindi cancellare il semipiano negativo nelle regioni dove
esiste. Notare che i punti isolati dove la funzione non è
definita sono rappresentati da linee continue nel
diagramma, a differenza dei punti dove cambia il segno, per
i quali usiamo una linea tratteggiata
−2
3
0
(radici ReF p308n48-49-50)
Domini di funzione Re Fraschini p. 17-23 segno p. 23-25
Esempio 11
Studiare dominio e segno della seguente funzione:
y = ln(2x 2 − 1)
Studio del Dominio
La funzione è un logaritmo naturale ed accetta solo valori
strettamente positivi dell’argomento, quindi :
2x 2 − 1 > 0
⇒x <−
+
2
2
∨x >
2
2
−
−1
−
2
2
+
−
2
0
2
2
1
2
2
2
Studio del Segno
Un logaritmo con base maggiore di 1 è positivo quando
l’argomento è anch’esso maggiore di 1. Più precisamente:
a >1
1
loga f (x ) ≥ 0 se f (x ) ≥ 1
loga f (x ) < 0 se 0< f (x ) < 1
0
0 <a <1
loga f (x ) ≤ 0 se f (x ) ≥ 1
loga f (x ) > 0 se 0< f (x ) < 1
0
1
2
quindi ln(2x − 1) ≥ 0 se:
2x 2 − 1 ≥ 1
⇒
2x 2 − 2 ≥ 0
⇒
−1 ≤ x ≤ 1
−
+
−1
+
1
(logaritmi ass. p309n57-58-59)
11
Esempio 12
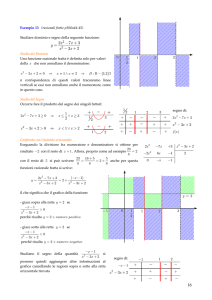
Studiare dominio e segno della seguente funzione:
y=
2x 2 − 7x + 3
x 2 − 3x + 2
Studio del Dominio
Una funzione razionale fratta è definita solo per valori
della x che non annullano il denominatore:
x 2 − 3x + 2 ≠ 0
⇒
x ≠ 1∧ x ≠ 2
0
1
2
D : ℝ − {1;2}
⇒
1
3
2
In corrispondenza di questi valori tracceremo linee
verticali se essi non annullano anche il numeratore,
come in questo caso.
Studio del Segno
Occorre fare il prodotto del segno dei singoli fattori:
2
2x − 7x + 3 ≥ 0
2
x − 3x + 2 > 0
⇒
⇒
−
+
1
x ≤ ∨x ≥3
2
1
3
2
−
+
x < 1∨x > 2
+
1
+
2
1
2
1
−
+
2x 2 − 7x + 3
+
−
−
+
+
x 2 − 3x + 2
−
+
−
+
f (x )
+
−
+
+
Confronto con l’asintoto orizzontale
Eseguendo la divisione fra numeratore e denominatore si ottiene per
23
risultato −2 con il resto di x + 1 . Allora, proprio come ad esempio
=2
8
23 16 + 5
5
=
=2+
anche per questa
con il resto di 5 si può scrivere
8
8
8
funzioni razionale fratta si scrive:
y=
segno di:
3
2
2x 2
−7x
+3
x 2 − 3x + 2
−2x 2
6x
−4
2
0
−x
−1
(−x − 1)
2x 2 − 7x + 3
=2+ 2
2
x − 3x + 2
x − 3x + 2
il che significa che il grafico della funzione:
−x − 1
>0
x − 3x + 2
perché risulta y = 2 + numero positivo
- giace sopra alla retta y = 2 se
y = 2
2
−1
0
1
2
1
3
2
−x − 1
<0
x − 3x + 2
perché risulta y = 2 + numero negativo
- giace sotto alla retta y = 2 se
2
−x − 1
si
x − 3x + 2
possono quindi aggiungere altre informazioni al
grafico cancellando le regioni sopra o sotto alla retta
orizzontale trovata
Studiano il segno della quantità
(razionali fratte p308n44-45)
2
segno di:
1
−1
2
−x − 1
+
−
−
−
x 2 − 3x + 2
+
+
−
+
+
−
+
−
12
y=
3x − 1
x +2


9
7
y = x 3 + x 2 + x − 3


2
2
2
13