1
Struttura atomica
Modello planetario di
Rutherford
2
Modello planetario
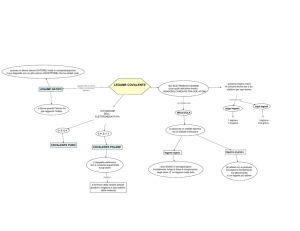
4 concetti chiave da comunicare:
1. Nuclei (carichi +) ed elettroni (carica -)
sono tenuti assieme da forze di tipo
elettrico -> Legge di Coulomb
F12 = k
q1q2
R2
2. I nuclei sono tenuti assieme da forze nucleari (diverse da
quelle di Coulomb, ruolo dei neutroni)
3. Le forze portano il sistema verso una situazione stabile che è
quella in cui si ha la minima energia
4. Negli atomi e nelle molecole questa tendenza è limitata da
altre regole -> quantizzazione
1
Modello planetario
3
Forze elettriche negli atomi:
1. Tutti gli elettroni in un atomo sono
attratti dal nucleo
2. La forza attrattiva che agisce su un
elettrone (dovuta al nucleo) dipende
dalla grandezza della carica nucleare
q1q2
e dalla distanza tra elettrone e
F12 = k
R2
nucleo
3. La forza attrattiva tra un elettrone e il nucleo agisce in
entrambe le direzioni (entrambi sentono la stessa forza)
4. Ogni elettrone respinge ogni altro elettrone con una forza
che dipende dalla loro distanza
Chemical Misconceptions
4
ed. Royal Society of Chemistry, UK
http://www.rsc.org/learn-chemistry/
Free material available at:
http://www.rsc.org/Education/Teachers/Resources/Books/Misconceptions.asp
2
Altro testo utile per la didattica della
chimica, scuola USA
5
Hands-On Chemistry Activities with Real-Life
Applications: Easy-to-Use Labs and Demonstrations
http://www.csun.edu/science/books/chemistry/index.html
6
Le più comuni credenze sbagliate di studenti > 16 anni:
• il nucleo NON è attratto dagli elettroni
• il nucleo attrae un elettrone più di quanto l’elettrone attrae il
nucleo
• i protoni nel nucleo attraggono un elettrone ciascuno
• gli elettroni respingono il nucleo
• gli elettroni sono responsabili del fatto che i protoni nel
nucleo restino assieme (che il nucleo non si spacchi)
• Gli elettroni non cadono sul nucleo perchè le forze di
attrazione verso il nucleo sono bilanciate dalle forze che
respingono il nucleo dagli elettroni
Da Chemical Misconceptions. Cap. 7 (2002) RSC editors
3
7
Analogia tra il modello atomico e il modello di un sistema solare
BUONA analogia didattica se:
• L’atomo è simile ad un sistema solare (ma ci sono delle
differenze)
• Gli studenti hanno familiarità con il sistema solare
• Gli studenti sono in grado di riconoscere le similitudini e le
differenze tra il modello di un atomo e il sistema solare
8
Esempio di questionario per gli studenti
4
Limitazioni del modello planetario per
l’atomo
10
Incompatibilità con le leggi classiche della fisica
(elettromagnetismo):
Una carica elettrica in moto non rettilineo uniforme perde
progressivamente energia emettendo radiazione.
L’elettrone collasserebbe sul nucleo seguendo una traiettoria a
spirale in 10-11 - 10-12 s.
L’atomo non è stabile secondo
la fisica classica!!
Dimensioni delle orbita arbitrarie -> non si vede perchè gli
atomi di uno stesso elemento sono tutti uguali
5
Andare oltre il modello planetario
11
Meccanica classica
1. Natura continua delle grandezze fisiche:
• Massa
• Carica
• energia
2. Prevedere il comportamento di atomi ed elettroni
risolvendo le equazioni del moto
Meccanica quantistica (rivoluzione scientifica 1900-1925)
1. Natura discreta delle grandezze fisiche
massa
atomi
carica
elettrone
energia
2. Particelle di dimensioni atomiche e subatomiche presentano
proprietà simili a quelle di un onda
La radiazione elettromagnetica
12
Radiazione elettromagnetica = campi elettrici e magnetici che
oscillano in direzioni perpendicolari tra loro e perpendicolari alla
direzioni di propagazione dell’onda (Maxwell 1865)
c ~ 300 000 km/s!!
6
13
Onde elettromagnetiche
λ⋅ν =c
Unità di misura: metro (m) e
sottomultipli, es. 1nm = 10-9m)
m/ciclo⋅cicli/s
= m/s
Unità di misura è il ciclo/s o
s-1 noto come Hertz (Hz)
λ =c/ν
ν = c/λ
14
Frequenza e lunghezza d’onda
Lunghezza d’onda (λ) e frequenza (ν) sono grandezze
inversamente proporzionali
numero d’onda
7
15
Ampiezza di un’onda
A parità di lunghezza d’onda (λ) le onde elettromagnetiche di
ampiezza superiore hanno intensità superiore
Regioni dello spettro elettromagnetico
FM
(10-100MHz)
16
AM
(102 kHz)
La luce visibile rappresenta solo una minima parte dello
spettro della radiazione elettromagnetica
8
Introdurre la meccanica quantistica come
fatto
17
1. Quantizzazione della radiazione e.m.
2. Quantizzazione dei livelli atomici
Esperimenti (inizi 1900) che non potevano essere
semplicemente spiegati dalla fisica classica:
Effetto fotoelettrico
quantizz. rad. em
Spettri a righe degli atomi
quantizz. liv atomici
Esperimento di Franck-Hertz
Radizione di corpo nero
quantizz. rad. em
18
Effetto fotoelettrico
Un piatto metallico carico
negativamente e sensibile alla
luce (fotocatodo) viene esposto
a radiazione luminosa di
frequenza ν e intensità variabili
•
•
•
•
OSSERVAZIONI:
Sotto una certa frequenza della luce
(frequenza di soglia) non succede nulla!
Sopra la soglia vengono emessi elettroni
dal fotocatodo con energia cinetica
proporzionale alla frequenza
Sopra la soglia al crescere dell’intensità della luce aumenta il
numero di elettroni emessi
Tutti i metalli subiscono questo effetto, ma le frequenze di
soglia sono differenti
9
Effetto fotoelettrico: la spiegazione di
Einstein
Non spiegabile dalla fisica classica:
19
E ∝ (ampiezza)2 ∝ Intensità
Spiegazione di Einstein (Nobel Prize 1921):
• la luce è costituita da particelle dette fotoni
• i fotoni possiedono energie quantizzate E=hν
• un fotone può trasferire la sua energia all’elettrone del metallo
• gli elettroni possono essere espulsi dal metallo solo quando sono
colpiti da fotoni con E0 ≥ hν0 sufficiente a vincere la forze che
tengono legati gli elettroni nel metallo
• energia del fotone = energia legame + energia cinetica
dell’elettrone emesso
Ecin= 1 mev22
2
ν<ν0
Ecin= 1 mev12
Ephot = hν
2
ν1≥ν0
Elegame = Φ = hν0 funzione lavoro
ν2>ν1
Ecin=1/2mev2
hν = hν0 + 1/2mev2
20
Conseguenze nella vita di tutti i giorni
•
Fotorivelatori (rivelatori di radiazione luminosa VIS,
UV) sono basati sull’effetto fotoelettrico
•
Reazioni fotochimiche (es. fotosintesi)
•
Celle fotovoltaiche
10
21
Spettri a righe degli atomi
Dispersione della luce bianca: la
luce solare può essere scomposta
nei vari colori generando uno
spettro a banda continua
spettro continuo
Tubo a scarica
contenente un gas
(H, Hg, Ne…)
Lo spettro generato dalla luce emessa da gas
in scariche elettriche (o alte T) non è
continuo, ma presenta delle righe a
determinate λ
spettro a righe
22
Spettri a righe degli atomi (emissione)
Gli spettri di emissione osservati sono caratteristici
dell’elemento contenuto nella scarica
H
Hg
Ne
Spettri atomici possono essere usati nell’analisi
chimica per l’identificazione di elementi (sono le
“impronte digitali” degli atomi)
11
23
Spettri a righe degli atomi (assorbimento)
Spettro di assorbimento
luce bianca emessa da
una sorgente attraversa
il campione che assorbe
in un insieme discreto di
lunghezze d’onda
Anche gli spettri di assorbimento presentavano delle
righe. La posizione in λ delle righe in assorbimento coincide
con quelle in emissione (in negativo)!
H
24
Spettro di emissione dell’atomo di H
(cm-1)
Nella regione del VIS
(Balmer 1885) le righe
1
1
15
apparivano a frequenze ν = 22 - n2 x3.29⋅10 Hz
date dalla formula:
n=3, 4, 5…
Es: per n=3 si ha ν=4.57⋅1014 Hz che corrisponde a λ=656nm
12
25
Modello atomico di Bohr
1. L’elettrone in un atomo di H può occupare solo orbite
specifiche attorno al nucleo
2. Ogni orbita ha una energia «quantizzata»
3. L’atomo non irradia energia luminosa quando l’elettrone
si trova su un’orbita
4. L’atomo emette (o assorbe) energia solo quando
l’elettrone salta da un’orbita ad un’altra (transizione
elettronica)
En = -
RH
con n=1, 2, 3, …
n2
numero quantico principale
RH = 2.18⋅10-18 J costante di Rydberg
26
Teoria di Bohr per l’atomo di H
Assorbimento
Ef
hν
Ei
En = -
RH
n2
hν = Ef-Ei
n = 1,2,3...
Emissione
Ei
E=hν
Ef
13
27
Teoria di Bohr per l’atomo di H
Energia
L’energia di interazione
elettrone-nucleo presenta il
valore minimo quando l’elettrone
r
è vicino al nucleo
(Ecoulomb∝ -e2/r).
n=3
n=2
Quando l’elettrone si allontana risale le
pareti del “pozzo” di energia potenziale.
n=1
Teoria di Bohr:
l’elettrone si trova sulle pareti del
pozzo solo per certi valori di E
Il modello di Bohr spiega gli spettri di
emissione dell’atomo di H
28
Gli spettri sono discontinui (a righe): ogni riga
corrisponde a un ben determinato valore di
energia, che a sua volta corrisponde alla
differenza di energia fra due orbite.
14
29
Origine degli spettri di emissione
Per passare dallo stato fondamentale ad uno eccitato l’elettrone
deve assorbire un fotone di energia hν appropriata
Ma l’eccitazione può anche avvenire tramite assorbimento di
energia in altra forma, es. energia cinetica per urto con altri atomi
o elettroni, o pareti recipiente (in generale per riscaldamento)
30
Limiti della teoria di Bohr
1. In realtà gli elettroni non si muovono su orbite circolari
2. Il modello funziona solo atomi che hanno un solo elettrone
attorno al nucleo (atomi idrogenoidi):
H, He+, Li2+, …
H (Z=1), He+ (Z=2), Li2+ (Z=3) ….
Il modello di Bohr anticipa il moderno modello della
struttura atomica basato sulla meccanica quantistica
15
31
Meccanica quantistica e struttura atomica
Meccanica quantistica
Teoria che sostituisce la meccanica classica nel caso di
particelle microscopiche, tenendo conto delle loro
proprietà andulatorie
radiazione elettromagnetica
Dualità onda-particella
particelle di materia
32
La radiazione elettromagnetica
Comportamento sia ondulatorio che corpuscolare
della radiazione elettromagnetica
Manifestazioni delle proprietà ondulatorie della
radiazione:
Interferenza
Diffrazione
onde in fase:
interferenza costruttiva
onde fuori fase:
interferenza distruttiva
16
33
La radiazione elettromagnetica
Manifestazioni delle proprietà
corpuscolari della radiazione:
Effetto fotoelettrico
La radiazione e.m. è costituita da pacchetti di energia detti
quanti o fotoni che si muovono alla velocità della luce
L’energia trasportata da ogni fotone dipende dalla frequenza
secondo la relazione di Planck:
L’energia associata ad un fascio di n
fotoni è una grandezza discreta E =
Quantizzazione della
radiazione e.m.
nhν
34
Le onde di de Broglie (1924)
Come le onde mostrano proprietà di particella anche le
particelle possono mostrare proprietà di onde
Ipotesi di de Broglie: al moto di qualunque particella
si accompagna la propagazione di onde
Diffrazione della
radiazione
elettromagnetica
Diffrazione di un
fascio di elettroni
Davisson, Germer, Thomson 1927
17
35
Onde associate a particelle
De Broglie: cosi come la radiazione e.m. è costituita da
particelle (fotoni) anche le particelle (e quindi gli elettroni)
possono avere le proprietà di un’onda
Relazione di de Broglie: λ = h/mv
h è la costante di Planck
Onde stazionarie: generazione di onde in
sistemi confinati
36
L
Solo alcuni modi di oscillazione sono
possibili, ovvero solo alcune λ sono
permesse:
n λ/2 = L
con n=1,2, 3, …
n=1 oscillazione fondamentale
n=2 prima armonica
n=3 seconda armonica
18
37
Le onde di de Broglie
De Broglie propone di
associare all’elettrone che
ruota attorno al nucleo
un’onda stazionaria
circolare
h
λ = m⋅⋅v
L’onda circolare può contenere solo un numero intero di λ
38
La λ di de Broglie di vari oggetti
h
λ = m⋅⋅v
19
39
Indeterminazione
momento p:
α
p =
h
λ
posizione:
angolo α
Conseguenza della relazione di de Broglie: il momento
(mv) e la posizione di un elettrone che ruota attorno al
nucleo non sono determinabili con precisione in maniera
simultanea
Principio di indeterminazione di
Heisenberg
40
Principio di indeterminazione di Heisenberg
non è possibile definire esattamente la posizione di un
elettrone quando questo si muove. Quanto più
precisamente viene determinata la posizione di una
particella, tanto meno precisamente può essere definita
la sua velocità (e viceversa)
∆x ⋅ ∆(m⋅⋅vx) = ∆x ⋅ ∆px ≥ h/4π
π
∆y ⋅ ∆(m⋅⋅vy) = ∆y ⋅ ∆py ≥ h/4π
π
∆z ⋅ ∆(m⋅⋅vz) = ∆z ⋅ ∆pz ≥ h/4π
π
h (costante di Planck)=6.63x10-34 J⋅⋅s
è un numero molto piccolo
p=m⋅⋅v
quantità di moto
20
Il principio di indeterminazione di
Heisenberg (1927)
41
L’indeterminazione è intrinseca nel processo di misura
“vedere” una palla
da baseball
fotone
-
“vedere” un elettrone
fotone
Traiettoria
indeterminata
Il principio di indeterminazione di
Heisenberg (1927)
42
Un fotone nel VIS ha una quantità di moto
p=h/λ
λ= 6.626⋅⋅10-34 J⋅⋅s /4⋅⋅10-7m = 1.66⋅⋅10-27kg⋅⋅m/s
Palla da baseball:
m=0.1 kg e v=100km/h
p=mv= 0.1 x 1⋅⋅105/3600 kg⋅⋅m/s =
= 2.8 kg⋅⋅m/s
fotone
pfotone <<< ppalla
-
fotone
Elettrone:
m=9.11⋅⋅10-31 kg e v=3⋅⋅106m/s
p=mv= 9.11⋅⋅10-31 x 3⋅⋅106 kg⋅⋅m/s =
= 2.7⋅⋅10-24 kg⋅⋅m/s
pfotone confrontabile con pelettrone
21
43
Teoria quantistica e struttura atomica
De Broglie
elettroni hanno
proprietà
ondulatorie
Heisenberg
Traiettorie precise non
sono ben definite per
sistemi piccoli
Abbandono dei concetti classici di traiettoria e orbita
(teoria di Bohr)
44
Modello quanto-meccanico dell’atomo
Meccanica quantistica: Teoria che sostituisce la meccanica
classica nel caso di particelle microscopiche, tenendo conto
delle loro proprietà andulatorie
• Elettrone in un atomo ha enegie «quantizzate»
• Non è possibile indicare l’esatta posizione di un elettrone
in un atomo in un dato istante, ma solo una PROBABILITA’
che l’elettrone si trovi in una certa posizione
•Si associa al moto dell’elettrone una funzione d’onda
Ψ(x,y,z) Il quadrato della funzione d’onda |Ψ(x,y,z)|2 dà la
probabilità di trovare l’elettrone nel punto di coordinate
(x,y,z)
• Le energie e le funzioni d’onda sono calcolate risolvendo
un’equazione matematica (equazione di Schrödinger)
22
45
La funzione d’onda Ψ e i numeri quantici
Le funzioni d’onda Ψ (funzioni matematiche),
soluzioni dell’equazione di Schrödinger, sono funzione
delle coordinate spaziali (x, y, z) e dipendono da
tre numeri interi (n, ℓ, mℓ) che si chiamano numeri
quantici
Ogni funzione d’onda definita da una particolare
terna di numeri quantici
(n, ℓ, mℓ) è chiamata
orbitale
Ogni orbitale corrisponde ad un possibile stato
quantico dell’elettrone
46
Orbite vs orbitali
e modello di Bohr
23
I numeri quantici
n: numero quantico principale
• Determina le dimensioni dell’orbitale e la sua energia
• Ha valori interi n= 1, 2, 3, ... ∞
• Elettroni con lo stesso n appartengono allo stesso livello
(shell)
ℓ: numero quantico azimutale
•
•
•
•
Indica la forma dell’orbitale
Influenza l’energia dell’orbitale
Assume i valori ℓ = 0, 1, 2, ...n-1
Elettroni con lo stesso ℓ appartengono
sottolivello (subshell)
allo
stesso
I numeri quantici
mℓ : numero quantico magnetico
• Determina l’orientamento dell’orbitale all’interno di un
sottolivello
• NON influenza l’energia dell’orbitale
• Assume valori interi compresi tra - ℓ e + ℓ
• Il numero di valori ammessi di mℓ dà il numero di orbitali in
un sottolivello
24
49
Numeri quantici e orbitali
n =1, 2, 3… ∞
ℓ =0, 1, 2, 3 … (n-1)
mℓ = - ℓ, -(ℓ -1), …0… +(ℓ -1), + ℓ
50
Forme degli orbitali
Per visualizzare gli orbitali si possono usare:
1. Superficie che delimita una regione si spazio entro la
quale l’elettrone ha una probabilità del 90% di essere
trovatorispetto al nucleo (superficie di equiprobabilità)
2. Rappresentazione (per punti o sfumatore di colore) della
distribuzione degli elettroni in un determinato istante
(nuvola elettronica)
3. Probabilità di trovare l’elettrone all’interno di un guscio
sferico di spessore infinitesimo posto a distanza r dal
nucleo (distribuzione di probabilità radiale)
25
51
Orbitali di tipo s (ℓ=0)
Gli orbitali s hanno simmetria sferica rispetto al nucleo
superficie di
equiprobabilità
nuvola elettronica
Distribuzione di probabilità radiale
52
Orbitali di tipo p (ℓ=1, ml=-1,0,+1)
Gli orbitali p hanno simmetria cilindrica rispetto ad un
asse e hanno una forma bilobata
2pz
2px
2py
Hanno un piano (perpendicolare all’asse di simmetria) in
cui la funzione d’onda si annulla
26
53
Orbitali di tipo d (ℓ=2, ml=-2,-2,0,+1,+2)
3dx2-y2
3dyz
3dxy
3dxz
3d z2
54
Osservazioni generali
• All’aumentare di n l’orbitale si ingrandisce e si
allontana dal nucleo
• Gli s hanno simmetria sferica, gli p hanno forma
bilobata, gli d hanno 4 lobi (o ciambella)
• Ci sono superfici (nodi) in cui non si possono
trovare elettroni (Ψ
Ψ si annulla)
27
55
Shell, subshell e orbitali
Livelli energetici degli orbitali atomici
dell’idrogeno
56
Il valore dell’energia dipende solo da n (numero quantico
principale)
Ad ogni n corrisponde un determinato livello energetico
(strato o guscio). Ogni guscio è individuato da una lettera
maiuscola: K (n=1), L(n=2), M (n=3)…
numero orbitali =n2
n2=16
n2=9
n2=4
n2=1
Orbitali che appartengono allo stesso livello energetico
(es. 2s e 2p, 3s-3p e 3d) si dicono degeneri
28
57
Peculiarità degli atomi plurielettronici
Il principio di esclusione di Pauli
Esiste un quarto numero quantico
ms: numero quantico di spin
• Elettrone
gira
su
sè
stesso
comportandosi come un piccolo magnete
• Può girare in senso orario o antiorario
• Il numero quantico di spin ha valori +1/2 o
-1/2
Principio di esclusione di Pauli
• Nessun orbitale atomico può contenere più di 2 elettroni
• I due elettroni nello stesso orbitale atomico non possono
avere lo stesso set di 4 numeri quantici (n,l,ml,ms)
“Ogni elettrone ha il proprio indirizzo”
29
59
Spin elettronico – numero quantico ms
Il magnetismo è il risultato macroscopico della
quantizzazione dello spin elettronico
Fe
30
61
Energie degli orbitali
Atomi di H o idrogenoidi
Energia dipende solo da n
(n. quantico principale)
Atomi plurielettronici
•Energia dipendono sia da n (n.q.
principale) che da l (n.q.
secondario)
• A partià di n l’energia varia
nell’ordine s<p<d<f
Effetti elettrostatici sulle energie degli
orbitali in atomi plurielettronici
• Nell’atomo di H l’energia dipende solo da n
• Nei sistemi idrogenoidi l’energia dipende
da n e da Z (carica nucleare)
• Negli atomi plurielettronici
l’energia dipende da n, Z e l
En,l = -
RHZeff2
n2
En =-
En =-
62
RH
n2
RHZ2
n2
Zeff o Z*: carica
nucleare effettiva
(efficace)
Z* è la carica nucleare di cui risente
effettivamente un elettrone di un atomo
polielettronico, tenendo conto della
presenza degli altri elettroni
31
Effetto di schermo degli elettroni sulla carica
nucleare
63
La repulsione tra due elettroni che
occupano lo stesso orbitale porta ad
un aumento dell’energia
E (He+) = -5250 kJ/mol
E(He) = -2372 kJ/mol
Gli elettroni interni (1s) schermano
quelli esterni (2s) dalla forza
attrattiva complessiva del nucleo,
rendendo l’orbitale con 2s di energia
superiore
Fattori che influenzano l’energia degli orbitali 64
in atomi plurielettronici
D
Distribuzione di
probabilità radiale
Effetto di penetrazione:
A parità di n (es. n=2) gli orbitali s hanno una capacità di
penetrazione verso il nucleo che gli orbitali con l ≠ 0 non hanno.
Quindi un elettrone in un orbitale 2s risente meno degli effetti di
schermo di altri elettroni con lo stesso n.
La carica efficace sentita dagli s è
maggiore: Zeff(ns) > Zeff(np) > Zeff(nd)
Ne segue che l’ordine delle
energie è: Ens < Enp < End
2p
r/a0
32
65
Principio dell’Aufbau (costruzione)
Regole: In un atomo nello stato fondamentale (quello a energia
più bassa)
1. Ogni elettrone che si aggiunge va ad occupare
l’orbitale a più bassa energia disponibile
2. Principio di Pauli: un orbitale può essere occupato al
massimo da 2 elettroni che avranno spin antiparallelo
3. Regola di Hund: il riempimento di un orbitale degenere
(=stessa energia) si ha soltanto se gli altri orbitali
degeneri sono già occupati da un elettrone (massima
molteplicità)
np
ha energia minore di np
Sequenza diagonale nell’ordine di riempimento
degli orbitali
7
8
6
7
8
5
6
7
8
4
5
6
7
3
4
5
2
3
66
1
n+l
33
67
Configurazioni elettroniche negli atomi
E’ l’elenco degli orbitali occupati da un atomo nel suo
stato fondamentale (ground state)
68
Configurazioni elettroniche negli atomi
34
69
Configurazioni elettroniche negli atomi
70
Configurazioni elettroniche negli atomi
35
71
Configurazioni elettroniche negli atomi
72
Configurazioni elettroniche negli atomi
1s
36
73
Configurazioni elettroniche negli atomi
74
Configurazioni elettroniche e Tavola Periodica
La configurazione elettronica di un elemento determina la
posizione che esso occupa nella Tavola Periodica
37
Relazione tra il riempimento degli orbitali e la75
Tavola Periodica
76
Elettroni di valenza vs interni
38
77
Elettroni di valenza vs interni - Esempi
[Kr] 4d105s25p4
78
Periodicità delle proprietà atomiche
Le proprietà chimiche e fisiche degli elementi dipendono
dalla loro configurazione elettronica
Molte proprietà degli atomi variano gradatamente
(periodicità) lungo il sistema periodico, perché
gradatamente varia il numero di elettroni di valenza
Proprietà periodiche:
•Dimensioni degli atomi (raggi atomici)
• Energia di ionizzazione
• Affinità elettronica
• Elettronegatività
39
79
Dimensioni atomiche
• Le dimensioni di un atomo sono determinate dalla
distribuzione degli elettroni attorno al nucleo (che diminuisce
gradualmente con la distanza dal nucleo)
• Non è possibile determinare sperimentalmente le dimensioni
di una atomo isolato
80
Trends nei raggi atomici (R)
R aumenta
R aumenta
R aumenta
scendendo lungo
il GRUPPO
R diminuisce da
sinistra a destra
nel
PERIODO
40
81
Raggi atomici
Andamento lungo il PERIODO:
andando da sin verso destra si ha un aumento della
carica nucleare efficace (carica media sentita
dall’elettrone in un guscio esterno dovuta a protoni +
effetto di «schermo» degli altri elettroni) e quindi
dell’attrazione nucleare che causa una contrazione delle
dimensioni dell’orbitale ( e quindi del raggio)
Andamento lungo il GRUPPO:
scendendo lungo il gruppo si occupa un orbitale
esterno con n (numero quantico) maggiore. Maggiore
è n, più grande è l’orbitale
82
Raggi ionici
41
83
Energia di ionizzazione (EI)
è la quantità di energia necessaria ad allontanare
l’elettrone più esterno da un atomo in fase gassosa,
formando un CATIONE
M (g) + EI → M+(g) + e-
0
energia
Esempio:
per l’atomo Mg(g) [Ne]3s2
EI è l’energia necessaria a
togliere uno dei due
elettroni 3s
E∞
E3,0
E2,1
E2,0
3s2
E1,0
1s2
2p6
2s2
84
Trends nelle energia di ionizzazione
Aumento
Aumenta lungo il periodo: perché aumenta la carica nucleare
efficace (elettrone maggiormente attratto dal nucleo, serve
più energia per portarlo via)
Diminuisce lungo il gruppo: perché aumenta il valore di n (=
aumenta il raggio atomico), gli elettroni più esterni sono più
distanti (= meno legati) ed è più facile strapparli
42
85
Affinità elettronica
E’ l’energia rilasciata nel seguente processo
(acquisizione di un elettrone da parte di un atomo
neutro):
M (g) + e- → M-(g) + AE
Diminuisce lungo il
gruppo: n aumenta –>
raggio atomico aumenta ->
elettrone va ad occupare
un orbitale che è più
lontano dal nucleo
Aumento
Aumento
Aumenta lungo il periodo: carica
nucleare efficace aumenta ->
aumenta l’attrazione del nucleo
per l’elettrone aggiuntivo
86
Elettronegatività
E’ la misura della capacità di un atomo (all’interno
di una molecola) di attirare verso di sè gli elettroni
di legame con un altro atomo
F è l’elemento più elettronegativo della Tavola Periodica
Elettronegatività è arbitraria (dipende dalla scala, non misurabile
direttamente) ma è molto utile per descrivere la formazione di
legami chimici
43
87
Aumento
Trends nelle elettronegatività
• Elementi con alta elettronegatività (non metalli) tendono ad
attirare elettroni per formare anioni
• Elementi con bassa elettronegatività (metalli) tendono a
cedere elettroni per formare cationi
88
Reazioni chimiche e periodicità
44