Eventi condizionati

Eventi condizionati
Quando si ha motivo di credere che il verificarsi di uno o più eventi
sia subordinato al verificarsi di altri eventi, si è soliti distinguere tra
eventi dipendenti (o condizionati ) e eventi indipendenti
A
Siano A e B due eventi di Ω : si definisce evento condizionato B
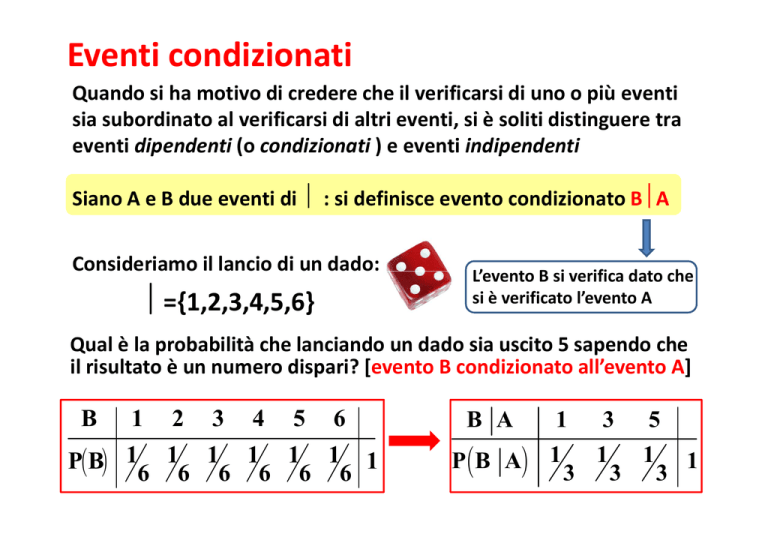
Consideriamo il lancio di un dado:
Ω={1,2,3,4,5,6}
L’evento B si verifica dato che
si è verificato l’evento A
Qual è la probabilità che lanciando un dado sia uscito 5 sapendo che
il risultato è un numero dispari? [evento B condizionato all’evento A]
B
1 2 3 4 5 6
P(B) 1 1 1 1 1 1 1
6 6 6 6 6 6
B A
P(B A)
1 3 5
1 1 1 1
3 3 3
Probabilità condizionate
P(B||A)=
n. dei casi favorevoli a (B ∩ A)
n. dei casi favorevoli a A
Ω
C
6
A
5
B
P(B ∩ A)
P(B|A) =
P(A)
1/6
=
1/2
Numeri
dispari
Si definisce probabilità condizionata di A dato B il rapporto tra
la probabilità dell’evento (A ∩ B) e la probabilità dell’evento B
Le probabilità devono essere ridefinite alla luce dell’evento
“il risultato è un numero dispari” (A) e riscalate in modo da
ottenere somma 1 (evento certo)
Principio delle probabilità composte
Dati 2 eventi compatibili A e B tali che P(A)>0 e P(B)>0
P (A ∩ B) = P(A) P(B|A) = P(B) P(A|B)
Due eventi si dicono indipendenti se il verificarsi di B
non influenza la probabilità di A e il verificarsi di A non
influenza la probabilità di B
P (A|B) = P(A)
Da ciò si ricava che:
P(B|A) = P(B)
P(A ∩ B ) = P(A ) ⋅ P(B )
La probabilità dell’evento intersezione A ∩ B, con A e B compatibili
e indipendenti, è uguale al prodotto delle probabilità di A e B
Esempio (eventi dipendenti)
Un’urna contiene 4 biglie bianche e 2 biglie nere. Si estraggono senza
reimmissione due biglie. Qual è la probabilità che entrambe le biglie
siano di colore bianco?
L’estrazione della prima biglia modifica lo spazio campionario
B1= prima biglia bianca
B2= seconda biglia bianca
 4  3  2
P ( B1 I B2 ) = P ( B1 ) ⋅ P ( B2 B1 ) =     =
 6  5  5
Probabilità di estrarre
una pallina bianca
Probabilità di estrarre una pallina bianca
dato che la prima pallina è bianca
40%
Esempio (eventi indipendenti)
In una gara di tiro al bersaglio il signor Rossi centra
mediamente 3 bersagli su 5 tiri. Su due tiri qual è la
probabilità che:
a) Centri due bersagli b) Non centri alcun bersaglio
c) Centri un bersaglio d) Centri almeno un bersaglio
La probabilità di far centro è data da casi favorevoli sui casi possibili:
E = centro il bersaglio => P(E) = 3/5
a) P(E1 ∩ E2) = P(E1)⋅⋅P(E2) = (3/5)⋅⋅(3/5) = 9/25
b) P(E1 ∩ E2) = P(E1)⋅⋅P(E2) = (2/5)⋅⋅(2/5) = 4/25
c) P(E1 ∩ E2) ∪ P(E1 ∩ E2) = (3/5)⋅⋅(2/5) + (2/5)⋅⋅(3/5) = 12/25
d) [P(E1 ∩ E2) ∪ P(E1 ∩ E2)] ∪ P(E1 ∩ E2) = (12/25) + (9/25)
Estrazione con e senza reimmissione
Supponiamo di avere un’urna con N palline numerate
1
La probabilità di estrarre una pallina è costante e pari a
N
Il reinserimento dopo l’identificazione ricrea a ogni
estrazione la situazione di partenza (eventi indipendenti)
La probabilità di estrarre una pallina varia ad ogni
estrazione e dipende dai risultati precedenti
Il non reinserimento dopo l’identificazione modifica a ogni
estrazione la situazione di partenza (eventi dipendenti)
Supponiamo di estrarre senza reimmissione due palline da un’urna che contiene 3
palline bianche e 7 nere. Qual è la probabilità di:
1) Estrarre una pallina bianca
e una pallina nera
 7  3 
P ( N1 I B2 ) = P ( N1 ) P ( B2 N1 ) =     = 0, 23
 10   9 
2) Estrarre due palline dello P N I N U P B I B =  7   6  +  3   2  = 0,53
( 1 2 ) ( 1 2 )      
stesso colore
 10   9   10   9 
Assiomi della probabilità condizionata
Le regole in base alle quali si calcola la probabilità che un evento
si verifichi devono valore anche per gli eventi condizionati:
Postulato 1
P [E | A] ≥ 0
Postulato 2
P [Ω | A ] = 1
Postulato 3
P ( E1 ∪ E2 ) | A =
= P [ E1 | A] + P [ E2 | A]
(E1 e E2 sono incompatibili)
Altre proprietà delle probabilità condizionate
Per gli eventi condizionati valgono le stesse proprietà viste per gli eventi
elementari:
1) Probabilità dell’evento contrario
P  E | H  = 1 − P [ E | H ]
2) Probabilità dell’evento differenza
P ( E1 − E2 ) | H  = P [ E1 | H ] − P ( E1 ∩ E2 ) | H 
3) Probabilità dell’evento unione (probabilità totali)
P ( E1 ∪ E2 ) | H  = P [ E1 | H ] + P [ E2 | H ] − P ( E1 ∩ E2 ) | H 
Esercizio
In un cassetto ci sono 10 lampadine di cui 6 funzionanti e 4
esaurite. Dal cassetto vengono prese a caso (in sequenza) 3
lampadine. Qual è la probabilità che le lampadine siano:
a) Tutti e tre funzionanti b) Tutte e tre esaurite
c) Due funzionanti e una esaurita d) Almeno una funzionante
 6  5  4  1
a) P(L1 ∩ L2 ∩ L3) = P(L1)⋅⋅P(L1|L2) ⋅P(L2| L2 ∩ L3) =       =
 10   9   8  6
 4  3  2  1
b) P(L1 ∩ L2 ∩ L3) = P(L1)⋅⋅P(L1|L2) ⋅P(L2| L2 ∩ L3) =       =
 10   9   8  30
1 1 1 1
c) P(L1 ∩ L2 ∩ L3) ∪ P(L1 ∩ L2 ∩ L3) ∪ P(L1 ∩ L2 ∩ L3) = + + =
6 6 6 2
d) ??? (la soluzione è ≈ 97%)
Probabilità condizionate su dati osservati (1)
E’ possibile calcolare le probabilità condizionate anche a partire da
dati osservati. Riprendiamo l’esempio sull’acquisto della TV:
Acquisto
Pianificato
Acquisto Effettivo
SI
NO
Totale
SI
200
50
250
NO
100
650
750
Totale
300
700
1000
Qual è la probabilità che l’acquisto della TV è stato effettuato nei
12 mesi dato che è stato pianificato?
P(acquisto effettuato | acquisto pianificato) =
che hanno pianificato ed effettuato l’acquisto
= n°n°soggetti
= n11/n1.
totale di soggetti che hanno pianificato l’acquisto
Probabilità condizionate su dati osservati (2)
Abbiamo detto che calcolare la probabilità condizionata significa
“riscalare” la probabilità relativa all’evento dipendente
P(acquisto effettuato | acquisto pianificato) =
= P(a. effettuato e pianificato) / P(a. pianificato) =
= (n11 / n)/(n1. / n) = (200/1000)/(250/1000)=200/250
La probabilità che un soggetto abbia acquistato una nuova
TV dato che aveva pianificato l’acquisto è pari a 0,8 (80%)
Qual è la probabilità che la TV è stata acquistata dato che l’acquisto non
era stato pianificato?
Qual è la probabilità che la TV non è stata acquistata dato che l’acquisto
era stato pianificato?
L’albero delle decisioni
Leggere la tabella può rivelarsi talvolta complicato, e allo stesso tempo è
facile confondere le differenti combinazioni di eventi. Un modo diverso di
rappresentare i dati è il cosiddetto albero delle decisioni
C
A
D
SOGGETTI
INTERVISTATI
Acquisto pianificato
ed effettuato (A ∩ C)
Acquisto pianificato
e non effettuato (A ∩ D)
C
Acquisto non pianificato
e d effettuato (B ∩ C)
D
Acquisto non pianificato
e non effettuato (B ∩ D)
B
Ad un gruppo di 173 studenti, suddiviso per genere, è stato chiesto qual è
il loro atteggiamento verso il fumo
Maschi
Femmine
Totale
Fumatore
16
19
35
Non Fumatore
80
58
138
Totale
96
77
173
C
Maschio Fumatore (A ∩ C)
D
Maschio non Fumatore (A ∩ D)
STUDENTI
A
C
Femmina Fumatrice (B ∩ C)
B
D
Femmina non Fumatrice (B ∩ D)
INDIPENDENZA STATISTICA
Nell’es. dei televisori:
La probabilità per un soggetto di acuistarlo è
pari a 0.3. Ma la stessa probabilità sale a 0.8 se
condizionata al fatto che il soggetto ha
pianificato l’acquisto.
La conoscenza a priori (in questo caso
rappresentata dalla previsione di acquisto)
influenza la probabilità.
Esiste il caso diametralmente opposto:
Indipendenza in probabilità (o stocastica)
DUE EVENTI E E F SONO INDIPENDENTI SE IL VERIFICARSI
DELL’UNO NON ALTERA LA PROBABILITA’ DELL’ALTRO
P ( E F ) = P (E )
l’evento E è stocasticamente indipendente da F
Tale interpretazione è coerente con la definizione di prob. Condizionata
P(E∩ F) P(E)* P(F)
P(E | F) =
⇒
= P(E)
P(F)
P(F)
Il fatto che uno studente sia fumatore
dipende o meno dal genere?
VERIFICA DELL’INDIPENZA
SUPPONIAMO I DATI SIANO:
Acquisto Effettivo
Acquisto
Pianificato
SI
NO
Totale
SI
75
175
250
NO
225
525
750
Totale
300
700
1000
P(ACQUISTO EFFETTIVO/ACQUISTO PIANIFICATO)=
75/1000: 250/1000=0.30
CHE COINCIDE CON LA PROBABILITA’ MARGINALE DELL’ACQUISTO