La scoperta di Maxwell: la corrente di
spostamento
Il lavoro dello scozzese James Clerk Maxwell (Glenlair 13 Giugno 1831 5 Novembre 1879) sulle equazioni dell'elettromagnetismo prese il via da una
situazione di discreto disordine. La formulazione delle celebri equazioni di
Maxwell come oggi la conosciamo era ancora lontana: all'epoca la descrizione
dei fenomeni avveniva attraverso una ventina di equazioni che coinvolgevano
diverse variabili, fra cui il potenziale magnetico vettore, poi abbandonato nelle
versioni successive 1 .
In realtà, fu l'inglese Oliver Heaviside (18 Maggio 1850 3 Febbraio
1925), elettrotecnico autodidatta, a sistemare le equazioni nella forma a noi
oggi familiare.
A ben vedere, il contributo più importante che Maxwell portò alla comprensione dei fenomeni elettromagnetici è senza dubbio l'introduzione del
termine denominato corrente di spostamento nella quarta equazione.
La situazione, al tempo (siamo attorno al 1860), si presentava all'incirca
così:
I
X Qk
E · dσ =
0
S
k, incl
I
dΦ(B)
E · dl = −
dt
Γ
I
B · dσ = 0
S
I
B · dl = µ0
Γ
X
ik
k,conc
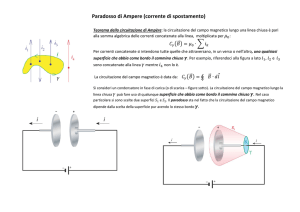
Maxwell ragionò così: se prendiamo in considerazione un semplice circuito
serie RC, costituito quindi da una resistenza R (non rappresentata in gura
per semplicità) in serie ad un condensatore C , a circuito aperto non passa
corrente (non è una grande scoperta).
L'approccio che utilizza il potenziale vettore è straordinariamente ecace per applicazioni di complessità superiore, ed è normalmente utilizzato in elettrodinamica
quantistica
1
1
Appena chiudo il circuito, inizia a scorrere una corrente di intensità decrescente (infatti alla forza elettromotrice della batteria si oppone il campo
controelettromotore dovuto al condensatore che va via via caricandosi). Allora, se applico il teorema di Ampère ad una curva Γ che contorna una
supercie che viene bucata dalla corrente i viaggiante nel lo, ottengo che la
circuitazione del campo B generato dalla corrente i è uguale a µ0 i.
Tutto giusto, tranne un piccolo particolare, che a Maxwell non sfuggì:
che cosa accade se, mantenendo ferma la curva Γ, deformo la supercie no
a farla chiudere tra le armature del condensatore?
2
Il campo B , ovviamente, non cambia (e come potrebbe, in fondo abbiamo
soltanto deformato la supercie); ci aspettiamo che il teorema di Ampére restituisca per la sua circuitazione il medesimo valore ottenuto poco fa, invece
no! Infatti, non vi è corrente tra le armature del condensatore! Ne consegue che la circuitazione restituita dal teorema di Ampére risulta, in questo
secondo caso, uguale a 0.
Non va bene: è del tutto evidente che manca qualcosa. Maxwell ragionò
a lungo sull'evidenza sperimentale, poi ebbe il colpo di genio: per simmetria,
pensò che, se la circuitazione del campo elettrico dipende dalla variazione
di usso del campo magnetico (legge di Faraday-Neumann-Lenz ), allora la
circuitazione del campo magnetico dipenderà dalla variazione del usso di E .
Per motivi dimensionali, scrisse il suo nuovo termine così:
dΦ(E)
dt
e si accorse che aveva le dimensioni di una corrente. la chiamò allora
displacement current, o corrente di spostamento. Con questa aggiunta, le
equazioni di Maxwell assumono la forma denitiva
I
X Qk
E · dσ =
0
S
k
I
dΦ(B)
E · dl = −
dt
Γ
I
B · dσ = 0
µ0 0
, incl
S
I
B · dl = µ0
Γ
X
k,conc
dΦ(E)
ik + 0
dt
o, in forma dierenziale,
∇·E =
ρ
0
∇·B =0
∇∧E =−
3
∂B
∂t
!
∂E
∇ ∧ B = µ0 j + 0
∂t
Le cose tornano a funzionare, infatti, tra le armature del condensatore
non vi è una corrente di conduzione, però c'è un campo elettrico variabile
che rimette a posto le cose.
Esiste anche un modo più . . . matematico di accorgersi che la quarta equazione di Maxwell è incompleta se privata del termine relativo alla corrente di
spostamento. Infatti, è noto che si ha identicamente
∇·∇∧B =0
in quanto la divergenza di un rotore, in ipotesi di regolarità, è identicamente nulla (si applica il teorema di Schwartz, ecco perché chiediamo la
regolarità). Formalmente, la dimostrazione si può conseguire anche così:
∇ ∧ B risulta per denizione ortogonale sia a ∇ che a B , ed il prodotto
scalare di un vettore per un altro vettore ad esso ortogonale è nullo.
Prendiamo allora in esame la quarta equazione nella sua forma provvisoria, preMaxwell, e calcoliamo la divergenza di entrambi i membri:
∇ · ∇ ∧ B = ∇ · (µ0 j) = 0
da cui segue immediatamente, essendo µ0 una costante che si può portare
a fattore fuori dal segno ∇,
∇·j =0
il che costituisce un assurdo, infatti, dall'equazione di continuità
∇·j =−
∂ρ
∂t
da cui
∂ρ
=0
∂t
cioè risulterebbe che la densità di corrente è per forza costante nel tempo,
e questo, in condizioni non stazionarie, è clamorosamente falso.
C'è di più: l'analisi vettoriale ci consente di ricavare matematicamente
l'espressione della corrente di spostamento. Vediamo come. Il teorema di
Gauss porge
4
ρ
0
vale a dire, derivando rispetto al tempo e riordinando,
∇·E =
∂
∂ρ
(∇ · E) =
∂t
∂t
In ipotesi di regolarità possiamo scambiare il simbolo ∇ col simbolo di
derivazione parziale, per cui
0
0 ∇ ·
∂ρ
∂E
=
∂t
∂t
∂ρ
,
∂t
∂E
0 ∇ ·
+∇·j =0
∂t
e, ricordando che ∇ · j = −
cioè
∂E
+ j) = 0
∂t
e ovviamente la storia non cambia se moltiplichiamo tutto per la costante
∇ · (0
µ0 :
∂E
)=0
∂t
ed ecco che abbiamo trovato l'espressione che ha le seguenti caratteristiche:
µ0 ∇ · (j + 0
1. ha divergenza nulla
2. è dimensionalmente corretta
3. si riduce a µ0 j in condizioni stazionarie
dunque è il secondo membro, nalmente completo, della quarta equazione
di Maxwell. Naturalmente, la Fisica non si fa con le sole dimostrazioni matematiche: la verica sperimentale, come al solito, ha l'ultima parola. Come
abbiamo visto nella parte iniziale di questo capitolo, l'evidenza sperimentale
da ragione a Maxwell.
5