LE EQUAZIONI
DI MAXWELL
James Clerk Maxwell :
diavolo d’un fisico!
Si
devono allo scozzese James Clerk Maxwell
l’unificazione dei fenomeni elettrici e magnetici grazie
alla teoria del campo elettromagnetico e a lui
importanti studi sui gas.
Nato nel 1831 a Edimburgo, in Scozia, da una famiglia
della piccola nobiltà terriera, Maxwell svolse la sua
attività scientifica per lo più a Cambridge, dove, negli
ultimi anni della sua vita, seguì anche la realizzazione
del Laboratorio Cavendish, un luogo destinato a
diventare celebre per le ricerche lì condotte
sull’elettrone e sul nucleo atomico.
Alla sua morte, nel 1879, il fisico lasciò trattati su elettromagnetismo e teoria
dei colori, sulla termodinamica, sulla teoria cinetica dei gas e persino su un
dispettoso e immaginario diavoletto che potrebbe far fuggire dal buco della
serratura tutte le molecole d’aria presenti in una stanza.
L’INTUIZIONE DI MAXWELL
Quando il flusso di
un campo
magnetico attraverso
un circuito subisce una
variazione nel tempo,
sappiamo dalla legge di
Faraday che il circuito si
vedrà attraversato da una
corrente elettrica.
D’altro canto, ci si può
chiedere se valga il
contrario: un campo
elettrico non stazionario
produce, nello spazio
attorno a sé, un campo
magnetico?
A dare una risposta a questo
interrogativo fu Maxwell che si
interrogò profondamente sulle
relazioni che intercorrono tra
campo elettrico e campo
magnetico.
L’intuizione di Maxwell era che le
interazioni reciproche tra campo
elettrico e campo magnetico
potessero essere spiegate da
un’unica teoria. Sulla base di
queste convinzioni, egli formulò
quattro famose equazioni che
spiegano completamente tutti
questi fenomeni: queste
equazioni sono il punto di
massimo sviluppo
dell’elettrodinamica classica.
LEGGE DI COULOMB
LEGGE DI AMPERE
•
LEGGE DI FARADAYNEUMANN-LENZ
Prima di Maxwell….
L’
Dimostrazione della legge di FaradayNeumann
F = Bil
Pd = f i
P = F t V/ t = BilV -> P = FV
f i = BilV -> f = BlV
em
em
em
La forza elettromotrice è costante nel tempo?
Il campo elettrostatico è conservativo: la
circuitazione è sempre nulla.
Il campo elettrico indotto non è conservativo: la
circuitazione dipende dal percorso compiuto.
Il teorema di Gauss per il
magnetismo
•
Il flusso del
campo
magnetico
attraverso
qualsiasi
superficie chiusa
è uguale a zero.
•
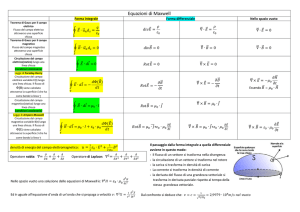
Per sfruttare la simmetria del campo B, calcoliamo la circuitazione lungo
un cammino circolare, di raggio r, che si sovrappone con una delle linee
del campo magnetico. In questo modo, come è mostrato nella figura, in
ogni tratto del cammino lo spostamento è parallelo al vettore Bj presente
in quella zona.
Si applica la formula
e
sostituendo l’angolo αj=0
(di conseguenza il cos
è uguale a 1),
per la legge di Biot-Savart :
dove d=r e considerando che quando tende l
all’∞ la sommatoria delle distanze diventa
la lunghezza 2πr della circonferenza
lungo cui è calcolata la circuitazione.
Otteniamo :
LA CORRENTE DI SPOSTAMENTO
Un campo elettrico variabile (corrente di
spostamento) genera un campo magnetico.
La legge di Ampere diventa :
Conosciuta come legge di Ampere-Maxwell