Le equazioni di Maxwell - Sito Personale di Ettore Limoli

Le equazioni di
Maxwell
Onde elettromagnetiche
di Ettore Limoli
Campo elettrico indotto
Estraendo una spira da un campo
magnetico, la forza di Lorentz, agendo sui
portatori di carica (elettroni) presenti nella
spira, genera una corrente indotta.
 Anziché considerare la corrente indotta
come causata da una f.e.m. indotta, la
possiamo considerare come causata da
un campo elettrico indotto.

Campo elettrico indotto




Indicando con q i portatori di carica, la forza di
Lorentz è: F = q v B sen.
Pertanto si ha un campo elettrico indotto:
E = F/q = v B sen
Il campo elettrico indotto è indipendente dai
portatori di carica.
La variazione del flusso del campo magnetico
genera un campo elettrico indotto diretto
secondo la corrente indotta.
Circuitazione del campo elettrico indotto

Calcolando la circuitazione
lungo una linea di campo l
(perpendicolare alla variazione
del flusso di B che l’ha
determinata si ha:
C (E) = v B l

Ossia la circuitazione è
uguale alla f.e.m. indotta.
C(E)  
d ( B)
(linea chiusa )
dt
l
Il paradosso del teorema di Ampere



Nel circuito in figura la
linea l delimita due
superfici A e B.
Attraverso la superficie A
(teorema di Ampere):
C(B) =  i
Attraverso la superficie B
(essendo i =0):
C(B) = 0
L
R
~
ƒ
l
C
Superficie A
Superficie B
La corrente di spostamento


Maxwell supera il
paradosso ammettendo
che all’interno del
condensatore vi sia una
corrente detta di
spostamento i*.
Pertanto la circuitazione è
data da:
C(B) =  ( i + i*)
L
R
~
ƒ
l
C
Superficie A
Superficie B
La corrente di spostamento

All’interno del condensatore, considerando le armature di area S,
per il teorema di Coulomb, si ha:
1 q
q
( E ) 
S
 S

da cui
q    ( E )
derivando :
dq
d ( E )
i* 

dt
dt
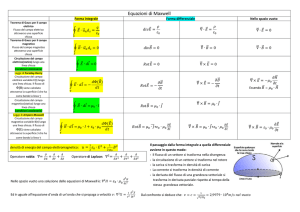
Le equazioni di Maxwell
1.
Teorema di Gauss: flusso di E attraverso una
superficie chiusa.
 (E) 
2.
q

Teorema di Gauss: flusso di B attraverso una
superficie chiusa.
 ( B)  0
Le equazioni di Maxwell
3.
Teorema di Ampere Maxwell: Circuitazione di
B lungo una linea chiusa.
 


dE
C B   i

dt

4.


Legge di Faraday-Neumann: Circuitazione di
E lungo una linea chiusa.
 

dB
C E 
dt
Le equazioni di Maxwell



Dalle quattro equazioni di Maxwell è possibile
dedurre tutte le leggi dell’elettromagnetismo.
Un moto accelerato di cariche, ad esempio,
genera un campo magnetico variabile
(equazione 3) che a sua volta genera un
campo elettrico variabile (equazione 4).
Nasce una perturbazione elettromagnetica
che si propaga nello spazio.
Onde elettromagnetiche



Sperimentalmente Heinrich Hertz fu il primo a
rivelare le onde elettromagnetiche.
Guglielmo Marconi, successivamente, fu il primo
ad ottenere la trasmissione di segnali tramite
onde elettromagnetiche.
La velocità di propagazione delle onde
elettromagnetiche è data da:
c
1
 0 0
 2,9979 108 m / s
Onde elettromagnetiche

La densità di energia del campo elettromagnetico
è data da:
1
1
2
W  0 E 
B2
2
2 0
Circuiti oscillanti (LC)

Applicando il 2° principio di Kirchoff ad un
circuito LC (induttivo-capacitivo), si ha:
di Q
L  0
dt C
ossia :
di
LC
Q0
dt
d 2Q
LC 2 Q0
dt
Circuiti oscillanti (LC)

Equazione differenziale del 2° ordine omogenea a coefficienti
costanti. La caratteristica ha radici immaginarie(<0), pertanto il suo
integrale generale è del tipo:
Q  A sen(t   )
essendo :
d 2Q
2


A

sen( t   )
2
dt
Pertanto :
1

LC
quindi il periodo è :
T  2
LC