Ver. 1.1 del 27/5/09
IL Potenziale elettrostatico
1) La forza elettrica è conservativa
Partiamo col verificare che la forza elettrica è conservativa, limitandoci inizialmente al
caso di cariche elettriche puntiformi.
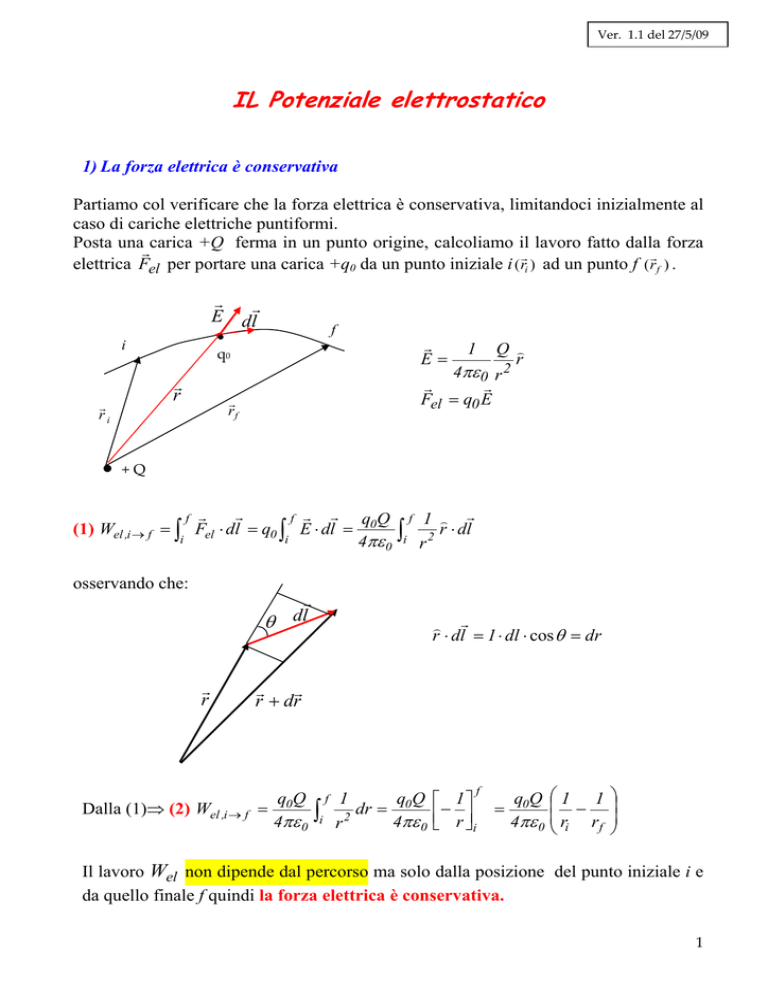
Posta unarcarica +Q ferma in un punto origine, calcoliamo il lavoro fatto dalla forza
r
r
elettrica Fel per portare una carica +q0 da un punto iniziale i ( ri ) ad un punto f ( r f ) .
r
r
E dl i
r
ri f
• q0 r
r
r
E=
Q )
r
4πε 0 r 2
r
r
Fel = q0 E
r
rf 1
• + Q r
r qQ
f r
f r
(1) Wel ,i → f = ∫ Fel ⋅ dl = q0 ∫ E ⋅ dl = 0
i
i
4πε 0
osservando che:
∫i
f
1 ) r
r ⋅ dl
r2
r
d
l
θ r
r Dalla (1)⇒ (2) Wel ,i → f
) r
r ⋅ dl = 1 ⋅ dl ⋅ cos θ = dr r
r
r + dr qQ
= 0
4πε 0
∫i
f
1
qQ
dr = 0
2
4πε 0
r
f
q0Q ⎛⎜ 1 1 ⎞⎟
⎡ 1⎤
=
−
−
⎢⎣ r ⎥⎦
⎜
4
πε
r
r f ⎟⎠
0 ⎝ i
i
Il lavoro Wel non dipende dal percorso ma solo dalla posizione del punto iniziale i e
da quello finale f quindi la forza elettrica è conservativa.
1
2) Energia potenziale elettrostatica
Si può quindi definire (vedi eq. 6 della lezione Energia Potenziale) una funzione
energia potenziale elettrostatica Uel = U. Dalla (2) segue:
r q Q ⎛ 1 1 ⎞ q Q 1 q0Q 1
f r
(3) ΔU el = − ∫ Fel ⋅ dl = 0 ⎜ − ⎟ = 0
−
i
4πε 0 ⎜⎝ r f ri ⎟⎠ 4πε 0 r f 4πε 0 ri
La variazione di energia potenziale dipende dalla posizione del punto finale f e del
punto iniziale i.
Poiché solo le differenze di energia potenziale hanno senso fisico, per semplificare le
relazioni si conviene di scegliere il punto iniziale i ovvero il punto di riferimento in
r r
qQ 1
r
ri = rrif = ∞ , ponendo U ( rrif = ∞) = 0 come conseguenza del fatto che 0
=0 .
4πε 0 ∞
Questo è coerente con l’osservazione che cariche molto distanti fra loro, praticamente
non interagiscono e quindi il contenuto di energia potenziale è nullo.
r q Q ⎛ 1 1⎞ q Q 1
f r
ΔU el = U el , f − U el ,∞ = U el , f − 0 = − ∫ Fel ⋅ dl = 0 ⎜ − ⎟ = 0
⇒
∞
4πε 0 ⎜⎝ r f ∞ ⎟⎠ 4πε 0 r f
(4)
r
qQ
U el ( r ) = 0 4πε 0 r
(per cariche puntiformi Q e q0)
L’energia potenziale della forza elettrostatica fra due puntiformi cariche Q ed q0è
data dalla eq. (4), posto che nel punto di riferimento (cariche a distanza infinita) sia
Uel(r=∞)=0. (Ricordarsi che Uel(r) è sempre una differenza rispetto al punto di
riferimento).
Significato: una carica q0 a distanza r da una carica Q ferma, ha una energia
potenziale che è il lavoro necessario alla forza elettrica per portare la carica q0 dalla
posizione r all’∞ ovvero (vedi oss. 3, lezione Energia Potenziale ) il lavoro fatto da
una forza applicata per portare la carica q0, con velocità costante, dall’∞ in
posizione r. L’energia potenziale elettrostatica è posseduta da una carica in quanto
occupa una posizione rispetto ad una altra carica con essa interagente (energia
associata alla configurazione del sistema).
2
r
r
Possiamo generalizzare il risultato precedente, ricordando che Fel = q0 E e quindi:
r
r
r
r
r
r r
r r
U el ( r ) = − ∫∞ Fel ⋅ dl = − q0 ∫∞ E ⋅ dl ⇒
(5)
r
r
r r
r
U el ( r ) = − q0 ∫∞ E ⋅ dl Si può dimostrare,
ma lo tralasciamo, che l’espressione (5), qui ottenuta perr un
r
campo E generato da una carica puntiforme, vale qualunque sia il campo E e
pertanto la (5) è l’espressione dell’energia potenziale elettrostatica di una carica q0
posta in un generico campo elettrico.
Osservazione: l’espressione (4) evidenzia che:
a) se le cariche hanno lo stesso segno, Uel è positiva,
b) se le cariche hanno segno opposto, Uel è negativa (come per potenziale
gravitazionale)
Questo è confermato avviamente dalla eq. 5. Infatti supponiamo di andare dall’∞ ad
r
un punto P a distanza r dalla carica Q lungo un percorso rettilineo coincidente con
r
la direzione di r (la forza elettrica è conservativa e quindi il percorso è irrilevante):
r r
a) dU el = −( + q0 )E ⋅ dl = − q0 Edl cos π = − q0 Edl( −1 ) = q0 Edl > 0 ,
r r
b) dU el = −( − q0 )E ⋅ dl = q0 Edl cos π = q0 Edl( −1 ) = − q0 Edl < 0 ,
P ● +Q
r
r
r
dl
r
E
∞
● ± q0
r
Questo si spiega ricordando che Uel rappresenta il lavoro fatto da Fap per portare la
carica da ∞ in r a velocità costante; tale lavoro è positivo se le cariche si respingono
(ovvero hanno lo stesso segno), negativo se le cariche si attraggono .
3
3) Il potenziale elettrostatico
Si definisce potenziale elettrostatico (V) l’energia potenziale elettrica per unità di
carica; ossia per qo= 1 C quindi:
r
r U el ( r )
r
r
V( r ) =
con V ( r ) = 0 per rrif = ∞
q0
r
r r
r
r
r
q
E
⋅ dl
r
∫
r r
∞ 0
V( r ) = −
= − ∫∞ E ⋅ dl
q0
⇒ (6)
r
r r r
r
V ( r ) = − E ⋅ dl ∫∞
r
r
r
V ( r ) è il lavoro fatto da Fap per portare una carica unitaria da ∞ a r in condizioni
di equilibrio.
lavoro 1 ⋅ J
=
= 1 ⋅Volt = 1 ⋅V
carica 1 ⋅ C
forza N N ⋅ m
J
V
CampoElettrico =
= =
=
=
carica C C ⋅ m C ⋅ m m
potenziale =
Unità di misura:
r
Ovviamente nell’espressione (6) il campo E è il campo totale dovuto a tutte le cariche
presenti nella zona di spazio considerato, ma allo stesso risultato si può giungere
sfruttando il principio di sovrapposizione. Infatti da quanto detto il potenziale dovuto
ad una carica puntiforme Q è dato da:
r
r r r
Q 1
r
V ( r ) = − E ⋅ dl =
⋅ ,
4πε 0 r
∞
∫
r
r
con V ( r ) = 0 per rrif = ∞
mentre, se abbiamo un insieme di cariche, il potenziale totale è la somma algebrica dei
potenziali delle singole cariche
r
1
Q
v
V ( r ) = ∑Vi ( r ) =
∑ i e al limite per una distribuzione continua di carica
4πε 0 i ri
i
r
r
r
1 dq
r r
V ( r ) = − ∫∞ E ⋅ dl = ∫ dV =
∫ , dove dq è la carica posseduta dal volume dV.
4πε 0 r
Osservazioni:
1) Il potenziale elettrico in un punto è una proprietà del punto in quanto sede del
campo elettrico e non dell’eventuale carica nel punto.
2) L’energia potenziale elettrica Uel è l’energia posseduta da una carica q0 posta in un
punto caratterizzato da un potenziale elettrico V con Uel = q0V
4
4) La differenza di potenziale elettrostatico
Più utile del valore del potenziale in un punto è la differenza di potenziale (d.d.p) ΔV
fra due punti.
La forza elettrica è conservativa e i percorsi non sono rilevanti, quindi scegliamo di
andare da ∞ ad f lungo un percorso passante per i e che fino ad i coincida con quello
usato per andare da ∞ ad i.
• f ∞ • i
ΔV = V f − Vi = −
i r r
i r r
f r r
i r r
r
E ⋅ dl − ( − E ⋅ dl ) = − E ⋅ dl −
E ⋅ dl + E ⋅ dl ⇒
f r
∫∞
(7) ΔV = V f − Vi = −
∫i
∫∞
r
E ⋅ dl
f r
∫∞
∫i
∫∞
definizione di d.d.p.
quindi la d.d.p. è il lavoro fatto da una forza applicata (l’opposto del lavoro di una
forza elettrostatica) per portare da un punto iniziale i ad un punto finale f una carica
unitaria in condizioni di equilibrio.
Se i ≡ f, ossia se la carica unitaria è spostata su un cammino chiuso Γ, essendo la forza
elettrica conservativa la d.d.p. è pari a zero cioè:
(8)
∫Γ
r r
E ⋅ dl = 0
detto: teorema della circuitazione per il campo elettrico.
La (8) esprime formalmente il fatto che il campo elettrico è conservativo
5
Osservazione#1
Calcoliamo
la d.d.p. fra due punti i ed f posti sulla stessa linea di campo, in un campo
r
E uniforme.
+
dl • i ‐
• f r r
La d.d.p. non dipende dal percorso ⇒ cammino lungo una linea di campo ⇒ E // dl
f r r
f
d .d . p = ΔV = V f − Vi = − E ⋅ dl = − Edl = − E ⋅ dif ⇒ ΔV = − E ⋅ dif
∫i
∫i
poiche E > 0 e la distanza da i ad f = dif >0 ⇒ ΔV = V f − Vi < 0
⇒
V f < Vi
Quindi il potenziale diminuisce spostandosi lungo le linee di campo, concordemente al
verso delle stesse.
Ricordando il verso del moto delle cariche in E, si osserva che:
• cariche positive di muovono spontaneamente verso potenziali decrescenti
• cariche negative di muovono spontaneamente verso potenziali crescenti
Osservazione#2
r
In una regione sede di un E , l’insieme dei punti dello spazio caratterizzati dallo stesso
potenziale elettrostatico costituisce una superficie equipotenziale.
Per percorsi su superfici equipotenziali sia ha per definizione ΔV = 0
f r r
r
r
r
r
⇒ ΔV = − E ⋅ dl = 0 ;
ma E ≠ 0, dl ≠ 0 ⇒ E ⊥ dl ⇒
∫i
le linee di campo sono perpendicolari alle superfici equipotenziali
6
Esempi di linee di campo e superfici equipotenziali:
Per campo uniforme:
Sistema di cariche opposte:
7
5) Il lavoro delle forze elettriche in termini di ΔV
Se si sposta una carica q0 fra una ΔV, le forze elettriche fanno un lavoro che può essere
scritto, usando la definizione di Uel e di ΔV, come:
Wel ,i → f = − ΔU el = − q0 ΔV , mentre Wap ,i → f = q0 ΔV
6) Calcolo del campo elettrico dal potenziale
r
E θ
El
V
f r r
ΔV = − E ⋅ dl ⇒
i
r r
dV = − E ⋅ dl ⇒
dV = − E ⋅ dl. cos θ = −( E ⋅ cos θ ) ⋅ dl
Da
r
dl V+ dV
∫
Indicando con El = E cos θ la componente
r
del campo lungo dl ⇒ dV = − El ⋅ dl ⇒ El = −
dV
dl
Ossia: in un punto la componente del campo in una direzione l generica è data dalla
variazione, cambiata di segno, del potenziale V su un piccolo spostamento lungo l.
r
Per il caso semplice di E uniforme, da (8) ⇒ E = −
ΔV
(con Δl = dif )
Δl
Esempio:
r
Il potenziale generato da una carica puntiforme Q in un punto r è:
r
V (r ) =
1 Q
⇒
4πε 0 r
r
dV ( r )
d
1 Q
Q d 1
Q
1
1 Q
−
=− (
)=−
( )=−
(− ) =
= Er
dr
dr 4πε 0 r
4πε 0 dr r
4πε 0 r 2
4πε 0 r 2
8
7) Un conduttore in equilibrio è equipotenziale
Consideriamo due percorsi
1 = tutto interno al conduttore
2 = sulla superficie del conduttore
r
Es
• i
•f
2
•f
1
• i
Percorso 1)
Percorso 2)
f r r
⇒ ΔV = − E ⋅ dl =
ri
ma E INT = 0 ⇒ ΔV = 0 ⇒ V f = Vi
∫
⇒ ΔV = −
∫i
r
ma E s
f r
r
r
E ⋅ dl = −
E s ⋅ dl
i
r
r
σ r
=
n ⇒ E ⊥ dl ⇒ ΔV = 0 ⇒ V f = Vi
f r
∫
ε0
In ogni caso V f = Vi e data la genericità dei punti i ed f ⇒ è vero per tutti i punti ⇒
il conduttore è equipotenziale.
9












