Appunto sui moltiplicatori keynesiani

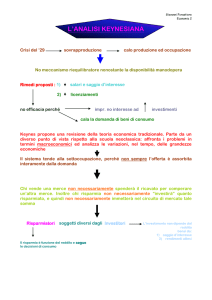
I moltiplicatori keynesiani
Economia chiusa senza settore pubblico.
Y = Pil
C = consumi
I = investimenti
Condizione di equilibrio (domanda aggregata = offerta aggregata):
Y=C+I
Funzione del consumo:
C= c0 + c1 Y
dove:
c0 = componente autonoma del consumo (non dipende dal reddito)
c1 = propensione marginale al consumo
Si fa l’ipotesi che I non dipenda dal reddito:
𝐼=𝐼
Modello di determinazione del reddito:
[1] Y=C+I
[2] C= c0 + c1 Y
[3] 𝐼 = 𝐼
Risolvendo per Y:
𝑌=
1
(𝑐 + 𝐼)
1 − 𝑐! !
𝑐! + 𝐼 = domanda autonoma
1 − 𝑐! = propensione marginale al risparmio
!
!!!!
= moltiplicatore
Esempio
c1=0,8
moltiplicatore = 5
Spiegazione del moltiplicatore. Se aumentano gli investimenti di ΔI, il Pil in un primo
momento aumenta dello stesso importo (dalla [1]). Per produrre i nuovi beni
d’investimento, le imprese generano un aumento dello stesso importo di salari e utili, cioè
1
di reddito. Una parte del maggior reddito, pari a (c1 ΔI), va in maggiori consumi. Nel
produrre i nuovi beni di consumo, le imprese distribuiscono un maggior reddito per lo
stesso importo, vale a dire (c1 ΔI); di seguito una quota pari a (𝑐!! ∆𝐼) va in maggiori
consumi. E così via.
Si avrà dunque:
[4] ∆𝑌 = ∆𝐼 + 𝑐! ∆𝐼 + 𝑐!! ∆𝐼 + ⋯ = 1 + 𝑐! + 𝑐!! + 𝑐!! + ⋯ ∆𝐼
1 + 𝑐! + 𝑐!! + 𝑐!! + ⋯ è una serie geometrica con termine iniziale 1 e ragione c1
Moltiplicando entrambi i lati della [4] per c1, otteniamo:
[5] 𝑐! ∆𝑌 = 𝑐! + 𝑐!! + 𝑐!! + ⋯ ∆𝐼
Sottraendo la [5] dalla [4]:
ΔY – c1 ΔY = ΔI
da cui:
∆𝑌 =
1
∆𝐼
1 − 𝑐!
Economia aperta con settore pubblico.
[1]
[2]
[3]
[4]
[5]
[6]
[7]
M+Y = C+I+G+E
C= c0 + c1 (Y-T)
T= ty Y
M=mY
𝐼=𝐼
𝐺 = 𝐺
𝐸 = 𝐸
Dove;
M = importazioni, che si suppone dipendano dal reddito;
m = propensione marginale all’importazione;
G = spesa pubblica per beni e servizi, determinate esogenamente;
T = imposte, che si suppone dipendano dal reddito;
ty = aliquota aggregata delle imposte;
E = esportazioni, determinate esogenamente.
Si ottiene:
𝑌 = 1
(𝑐 + 𝐼 + 𝐺 + 𝐸)
1 + 𝑚 − 𝑐! (1 − 𝑡! ) !
2