ΔH = SPONTANEITÀ ? NO!!!!!!!
Se ΔH°reaz determinasse la DIREZIONE SPONTANEA del PROCESSO:
a)
Tutte le reazioni esotermiche sarebbero spontanee
b)
Tutte le reazioni endotermiche sarebbero non spontanee.
c)
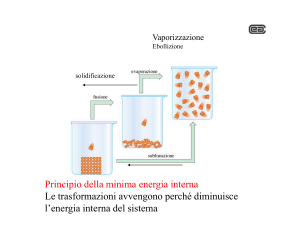
La materia sarebbe tutta allo stato solido, perchè il passaggio dallo stato gassoso allo stato
liquido è un processo esotermico, così come il passaggio da liquido a solido: minore energia
termica e massimo ordine.
Invece, in natura si hanno molte trasformazioni fisiche e reazioni chimiche che avvengono
spontaneamente pur essendo endotermiche (ovvero pur andando in salita dal punto di vista
energetico!). Ad esempio il carbonato di Calcio (CaCO3) ad una data temperatura si decompone
spontaneamente, così come il ghiaccio fonde spontaneamente a T > 0°C
Esistono quindi molti processi che avvengono IN SALITA SPONTANEAMENTE ⇒ IRREVERSIBILE (in
un’unica direzione), per cui l’idea che un SISTEMA TERMODINAMICO tenda a DIMINUIRE
SPONTANEAMENTE la propria energia è TROPPO SEMPLICISTICA e la situazione REALE è più
COMPLESSA.
Consideriamo due processi (a e b) aventi ΔH = 0:
1 - ESPANSIONE DI UN GAS IDEALE NEL VUOTO A T = COSTANTE
T = cost. poichè E del gas dipende solo dalla temperatura si ha che E1 = E2
quindi ΔEsist = 0. Inoltre P = 0 perchè l’espansione avviene nel vuoto, quidi PΔV
= 0. Ne consegue che ΔH = ΔE + PΔV = 0
ΔEuniv = ΔEsist + ΔEamb ΔEsist = 0, ΔEamb = 0 ⇒ ΔEuniv = 0
QUINDI Euniv = costante: 1° PRINCIPIO RISPETTATO, MA!!! SAREBBE
RISPETTATO ANCHE SE AVVENISSE IL PROCESSO CONTRARIO: non ci
sarebbe contrasto con il 1° principio se, aperta la valvola il gas rimanesse
confinato in A oppure se una volta espanso in B il gas ritornasse in A!
IL 1° PRINCIPIO NON DÀ INDICAZIONE SULLA SPONTANEITÀ!
vuoto
A
B
E1
E2
vuoto
IRREVERSIBILE
SPONTANEITÀ
2 - DUE GAS IDEALI DIFFONDONO SPONTANEAMENTE L’UNO NELL’ALTRO
Trattandosi di gas ideali le forze intermolecolari sono nulle, quindi il ΔHmescolamento = 0 per T = costante
Stato ordinato (minor probabilità)
Dispersione
MATERIA
Gas A + Gas B
evolve
miscela omogenea A + B
Stato di maggior disordine
(maggior probabilità)
Nei casi 1 e 2 considerati ΔH = 0 (sistema isolato). Quindi:
per un SISTEMA ISOLATO, la DIREZIONE SPONTANEA porta ad una MAGGIORE DISPERSIONE DELLA
MATERIA e dunque ad un AUMENTO DI DISORDINE DEL SISTEMA
PER UN SISTEMA CHIUSO (ΔH < o > 0) occorrerà confrontare:
I)
II)
come si disordina il SISTEMA (dispersione materia)
come si disordina l’AMBIENTE (dispersione energia)
Fe
CALDO
CALORE
Spontaneamente
se TFe > Tamb
Fe
FREDDO
Perchè il pezzo di Ferro caldo si raffredda fino a raggiungere la temperatura ambiente?
ENERGIA TERMICA CONCENTRATA VIENE TRASFERITA
(nel SISTEMA Fe)
TRAMITE CALORE
DISORDINE SISTEMA Fe
DIMINUISCE (POCO)
DIREZIONE
SPONTANEA
ENERGIA TERMICA DISPERSA
(nelle molecole d’aria dell’AMBIENTE)
DISORDINE AMBIENTE
AUMENTA (MOLTO)
(maggior dispersione di energia o meglio energia
dispersa su maggior numero di particelle)
Qual è allora la caratteristica comune che rende i processi citati spontanei in un’unica direzione?
La si individua considerando questi processi dal punto di vista microscopico.
1 - LA MATERIA TENDE A DIVENTARE PIÙ DISORDINATA (NEL SISTEMA)
2 - L’ENERGIA TENDE A DISPERDERSI SU UN MAGGIOR NUMERO DI PARTICELLE (NELL’AMBIENTE).
SPONTANEITÀ
STATO INIZIALE
(sistema + ambiente)
Spontaneamente
evolve verso
STATO FINALE
(sistema + ambiente)
Lo stato finale è più probabile
(maggior disordine di materia
e/o energia) di quello iniziale.
COME AVVIENE?
a)
aumentando il disordine delle particelle = disordine spaziale ≡ DISPERSIONE MATERIA:
REAZIONE DISORDINANTE
b)
Disperdendo l’energia su un numero maggiore di particelle ≡ DISPERSIONE ENERGIA: REAZIONE
ESOTERMICA
1.
2.
3.
Se in una reazione chimica si verificano entambi i processi (reazione disordinante ed esotermica)
la reazione è SEMPRE SPONTANEA.
Se non si verifica nè dispersione di materia nè di energia (reazione ordinante ed endotermica) la
reazione NON AVVIENE MAI.
Se si verifica una sola condizione la TEMPERATURA è DETERMINANTE per sapere quale dei due
effetti è maggiore: a basse T prevale DISPERSIONE DI ENERGIA, ad alte T prevale DISPERSIONE
MATERIA.
ENUNCIATI DEL SECONDO PRINCIPIO DELLA
TERMODINAMICA
•
TUTTI I PROCESSI SPONTANEI SONO IRREVERSIBILI
•
DOPO OGNI PROCESSO SPONTANEO, PER RIPRISTINARE IL SISTEMA NELLO STATO INIZIALE,
DEL LAVORO DEVE ESSERE TRASFORMATO IN CALORE
•
IN UN PROCESSO SPONTANEO AUMENTA IL DISORDINE
•
IL DISORDINE DELL’UNIVERSO È IN AUMENTO
ENTROPIA ASSOLUTA S
Misura della dispersione della materia (o disordine spaziale) in un campione di sostanza (≡ SISTEMA)
Esempio:
Consideriamo 4 molecole di
gas che si espandono nel
vuoto; vogliamo valutare il
numero di distribuzioni
possibili D(i,j) e il numero di
modi N con cui si realizza
una singola distribuzione.
3
1
4
2
3
1
3
2
4
2
4
1
3
1
4
2
D(4,0); D(0,4); N= 2
3
1
4
3
4
2
1
2
1
2
4
3
4
1
3
4
2
3
2
1
3
4
3
1
2
4
2
1
3
1
3
4
D(3,1); N = 4
4
2
1
2
3
2
1
4
D(1,3); N = 4
1
3
2
3
4
4
1
2
D(2,2); D(2,2); N= 6: distribuzione più probabile: 6 su 16.
La probabilità di esistenza di un particolare macrostato dipende dal numero di microstati da cui può
essere ottenuto: maggiore il è n° di microstati, maggiore è la probabilità W, maggiore è l’entropia S
Microstati sono le configurazioni (i modi) che si possono realizzare per avere una determinata
disposizione (combinazione), ovvero per avere un macrostato. Al numero di microstati che
compongono un determinato macrostato viene dato il nome di probabilità termodinamica W.
La relazione di Boltzman lega l’entropia alla probabilità: S = k lnW
Rappresenta il legame tra il mondo macroscopico della materia ed il mondo microscopico degli atomi e
molecole.
spontaneo
STATO INIZIALE
STATO FINALE
(stato meno probabile, con minore S)
(stato più probabile, con maggiore S)
irreversibile
Mazzo di carte ordinato per seme:
1 microstato
W = 1; S = klnW = 0
ΔS > 0
Mazzo disordinato mescolato a caso:
n microstati
W > 1; S = klnW > 0
3° PRINCIPIO DELLA TERMODINAMICA (NERNST)
Per l’entalpia H si era trovato utile scegliere un determinato stato della materia (stato standard) ed
assegnargli un definito valore dell’entalpia di formazione: H°f = 0 per le sostanze elementari a P = 1 atm
e T = 298 K (25°C). Per l’entropia S la situazione è diversa perchè l’associazione con i microstati
suggerisce una scelta “naturale” dello “zero” dell’entropia:
Per T → 0 K (-273,15°C) l’entropia tende a un valore costante prossimo a 0 (S → 0) indipendentemente
dalla pressione, stato di aggregazione, modificazione cristallina.
UN CRISTALLO PERFETTO ALLO ZERO ASSOLUTO HA ENTROPIA S UGUALE A ZERO
T→0K
NEON
ΔSevap.
ΔSfusione
T=0K
Ogni specie chimica ha Entropia finita e positiva,
funzione crescente della temperatura T
Cristallo 1) Aumentando T aumenta l’agitazione termica
perfetto (moti rotazionali, traslazionali, vibrazionali)
quindi aumenta il n° di microstati, aumenta S
e il campione si disordina.
2) È possibile determinare sperimentalmente S delle
sostanze a qualsiasi temperatura.
a) S = 0 allo zero assoluto;
b) S = f(T) quindi Ssolido < Sliquido << Sgas
c) S aumenta bruscamente nei passaggi di stato
d) ΔSevap. > ΔSfusione
3) Se l’entropia di una mole di sostanza è determinata
a 25°C (298 K) e alla pressione di 1 atm è chiamata:
S° = ENTROPIA MOLARE STANDARD
Questi valori sono tabulati. S° aumenta con la MASSA
delle sostanze: maggior moti rotazionali e vibrazionali
3° PRINCIPIO DELLA TERMODINAMICA (NERNST)
4) L’ENTROPIA È UNA FUNZIONE DI STATO
Se consideriamo una trasformazione nelle condizioni di reversibilità, possiamo calcolare la variazione
di entropia come ΔS = Qrev/T, dove Qrev è il calore fornito alla sostanza e T è la temperatura a cui è stato
aggiunto.
Possiamo comprendere ciò sulla base del seguente ragionamento: in un sistema di molecole tenute
insieme da forze attrattive, aggiungendo calore si crea più disordine, il che fa muovere le molecole più
violentemente.
In un cristallo, per esempio (come può essere un cubetto di ghiaccio a 0°C), le molecole vibrano intorno
alle loro posizioni di equilibrio nel reticolo, così che, in realtà, in ogni istante si ha un insieme di
particelle “non abbastanza ordinate”. Aggiungendo calore aumenta il movimento molecolare che
provoca un maggiore disordine istantaneo. In altre parole, se potessimo congelare il movimento delle
molecole, come un’istantanea fotografica, potremmo vedere che dopo aver aggiunto calore esiste un
disordine maggiore e quindi un’entropia più grande.
Questo aumento di entropia è direttamente proporzionale alla quantità di calore aggiunto
Tuttavia, se questa quantità di calore viene aggiunto a bassa T, dove esiste poco disordine, l’effetto è
più evidente rispetto a un’aggiunta ad alta T, dove esiste già un sostanziale disordine.
Per una data quantità di calore la variazione di
entropia è inversamente proporzionale alla T a cui
il calore viene aggiunto
ΔS = Qrev/T
Unità di misura cal/K o J/K
N.B.: l’entropia S aumenta all’aumentare di T mentre la variazione di entropia ΔS diminuisce
all’aumentare di T.
ΔS° PER UN SISTEMA
≡ variazione di entropia dovuta alla DISPERSIONE della MATERIA
ΔS°
variazione di entropia che avviene nel corso di una reazione chimica, quando i reagenti nel
loro stato standard (1 atm, 25°C) sono completamente trasformati in prodotti, anch’essi nel
loro stato standard
ΔS°SISTEMA = ΔS°reaz = ∑ S°prodotti - ∑ S°reagenti
Es 1:
ΔS° per la corrosione del Ferro
4 Fe(s) + 3 O2
2 Fe2O3 (s)
ΔS°reaz = 2 x S° (Fe2O3) – [4 x S°(Fe(s)) + 3 x S°(O2(g))] = - 549 J/K
ΔS°reaz ≡ ΔS°sist < 0 (il SISTEMA SI ORDINA: REAZIONE ORDINANTE)
Es 2:
ΔS° per la decomposizione di CaCO3
CaCO3(s)
CaO(s) + CO2(g)
ΔS°reaz = S° (CaO(s)) + S°(CO2(g)) – S°(CaCO3(s)) = 158,9 J/K
ΔS°reaz ≡ ΔS°sist > 0 (il SISTEMA SI DISORDINA: REAZIONE DISORDINANTE)
Es 3:
ΔS° passaggio di stato
H2O(l)
H2O(s)
ΔS°reaz = S° (H2O(l)) – S°(H2O(l)) = - 22 J/K < 0 REAZIONE ORDINANTE
N.B.: si può qualitativamente PREVEDERE il SEGNO di ΔSsistema (>, <, = 0) in una trasformazione.
1 - TRASFORMAZIONI CHE PORTANO AD UN AUMENTO DI ENTROPIA DEL SISTEMA (ΔSSISTEMA > 0)
A - Tutte le trasformazioni in cui le moli di sostanze allo stato gassoso aumentano passando da
reagenti a prodotti (vedi Es. 2)
B - I processi di fusione, evaporazione e sublimazione.
SOLIDO
LIQUIDO
GAS
ΔS° PER UN SISTEMA
2)
Trasformazioni che comportano una riduzione di entropia del sistema (ΔSsistema < 0)
Tutte le trasformazioni in cui le moli di sostanze allo stato gassoso diminuiscono passando da
reagenti a prodotti :
N2 (g) + 3 H2 (g)
2 NH3 (g)
ΔSsistema < 0
CH3OH (g)
ΔSsistema < 0
CO2 (g) + 2 H2 (g)
NH4Cl (s)
ΔSsistema < 0
NH3 (g) + HCl (g)
H2O(l)
H2O(s)
ΔSsistema < 0
H2O(v)
3)
Trasformazioni che comportano variazioni di entropia difficilmente valutabile o trascurabile
(ΔSsistema = 0)
a)
Trasformazioni che non coinvolgono sostanze allo stato gassoso
Fe2O3 (s) + 2 Al (s)
2 Fe (g) + Al2O3 (s)
b)
Trasformazioni che non presentano variazioni di moli in fase gassosa
CH4 (g) + 2 O2 (g)
CO2 (g) + 2 H2O (g)
ΔSsistema ~ 0
SISTEMA:
a)
b)
c)
ΔSsistema ~ 0
Corrosione del ferro:
Sintesi ammoniaca:
Congelamento H2O:
4 Fe(s) + 3 O2
N2 (g) + 3 H2 (g)
H2O(v)
H2O(l)
2 Fe2O3 (s) TUTTI PROCESSI SPONTANEI CHE
AVVENGONO CON DIMINUZIONE DI
2 NH3 (g)
DISORDINE DELLA MATERIA
H2O(s)
MA!! IL 2° PRINCIPIO DELLA TERMODINAMICA DICE CHE IL VERSO DEI PROCESSI SPONTANEI È
QUELLO PER CUI SUNIVERSO UMENTA: ΔSUNIVERSO > 0
(l’entropia dell’Universo aumenta a causa dei processi spontanei che in esso avvengono)
ΔSUNIVERSO = ΔSSISTEMA + ΔSAMBIENTE
ΔSsistema ≡ ΔS°reazione e si calcola da S° tabulati. Quindi, per i processi spontanei ordinati (ΔSsistema < 0)
dovrà esserci un ΔSambiente (aumento del disordine dell’ambiente) MAGGIORE della diminuzione di
disordine del sistema: ΔSambiente > - ΔSsistema
SEGNO DI ΔSUNIVERSO
Dobbiamo chiarire il ruolo di ΔSsistema e di ΔSambiente nel determinare il segno di ΔSuniverso
A)
La variazione di ΔSsistema dipende dalla variazione di entropia posizionale nel passaggio da
reagenti a prodotti e, come visto, si calcola dai valori S° tabulati. Ma questa è solo la prima parte
del calcolo:
DISORDINE DI POSIZIONE
DISPERSIONE DELLA MATERIA
B)
Vediamo ora come si calcola ΔSambiente: la sua variazione dipende dalla variazione di entropia (ΔH)
dovuta agli scambi di energia tra sistema e ambiente:
DISORDINE DI MOVIMENTO
DISPERSIONE DELL’ENERGIA
PROCESSO ESOTERMICO (ΔHSIST < 0): il calore sfugge verso l’ambiente intensificando
l’agitazione termica. ΔSambiente aumenta. ΔSambiente > 0
PROCESSO ENDOTERMICO (ΔHSIST > 0): l’energia, sotto forma di calore, viene prelevata
dall’ambiente, diminuendone l’agitazione termica. ΔSambiente diminuisce. ΔSambiente < 0
i)
ii)
Se lo scambio di energia fra sistema e ambiente, sotto forma di calore, avviene lentamente (a P e T cost)
Qrev = Qamb = ΔHamb = -ΔHsist
Quindi il disordine provocato nell’ambiente è proporzionale a - ΔHsist
ΔSAMBIENTE ∝ - ΔHSIST
A parità di calore scambiato ΔSamb dipende anche dalla TEMPERATURA a cui avviene lo scambio :
iii)
AMBIENTE CALDO (= DISORDINATO): l’afflusso di calore (- ΔHsist) provoca MODESTO aumento di
disordine dell’ambiente.
iv)
AMBIENTE FREDDO (= + ORDINATO): l’afflusso di calore (- ΔHsist) provoca CONSIDEREVOLE
aumento di disordine dell’ambiente.
ΔSAMBIENTE = - ΔHSIST /T
SEGNO DI ΔSUNIVERSO
Ora siamo in grado di capire perchè la corrosione del ferro (ΔS°sist = - 549 J/K → reazione ordinante) è
spontanea a 25°C e 1 atm.
4 Fe(s) + 3 O2
2 Fe2O3 (s)
ΔS°sist = ∑S°prod - ∑S°reag = -549 J/K < 0 (ORDINANTE)
ΔS°amb = - ΔH°sist/T = - ΔH°reaz/298 K
ΔS°univ = ΔS°sist + ΔS°amb
ΔH°reaz = ∑ΔH°f (prod) - ∑ΔH°f (reag) = - 1644 kJ/mol (ESOTERMICA: calore rilasciato all’ambiente)
ΔS°amb = - (- 1644 kJ)/298 K = + 5,518 kJ/K
ΔS°univ = - 549 J/K + 5518 J/K = 4969 J/K > 0 spontanea a 25°C e 1 atm
Quindi l’elevata esotermicità della reazione (che si cela dietro ΔS°amb) compensa il maggiore ordine
del sistema nel passaggio da reagenti ai prodotti (che si cela dietro ΔS°sist).
Il 2° PRINCIPIO fornisce la DIREZIONE DEL PROCESSO SPONTANEO e spiega perchè:
a)
Reazioni ESOTERMICHE (ΔHsist < 0) e DISORDINANTI (ΔSsist > 0) sono SEMPRE SPONTANEE.
b)
Reazioni ESOTERMICHE (ΔHsist < 0) e ORDINANTI (ΔSsist < 0) sono SPONTANEE a patto che
l’ambiente si disordini più di quanto si ordina il sistema (favorite a T relativamente basse).
c)
Reazioni ENDOTERMICHE (ΔHsist > 0) e DISORDINANTI (ΔSsist > 0) sono SPONTANEE a patto che
il sistema si disordini più di quanto si ordina l’ambiente (favorite a T relativamente alte).
d)
Reazioni ENDOTERMICHE (ΔHsist > 0) e ORDINANTI (ΔSsist < 0) non sono MAI SPONTANEE.
ENERGIA LIBERA DI GIBBS
L’ENTROPIA DELL’UNIVERSO AUMENTA A CAUSA DEI PROCESSI SPONTANEI (IRREVERSIBILI) CHE
VI SI SVOLGONO INESORABILMENTE
CRITERIO DI SPONTANEITÀ: ENERGIA LIBERA DI GIBBS
(OSSIA 2° PRINCIPIO VISTO DAL SOLO SISTEMA)
C’è un modo molto più comodo per i chimici per prevedere se una reazione può avvenire o meno
spontaneamente: partendo da proprietà del solo sistema e tenendo conto del fatto che le reazioni si
svolgono soprattutto a P e T costanti. Ciò induce ad un nuovo criterio di spontaneità basato su una
nuova funzione di stato: L’ENERGIA LIBERA G.
ΔSuniv = ΔSsist + ΔSamb > 0 MA ΔSamb = - ΔHsist/T ⇒ ΔSuniv = ΔSsist - ΔHsist/T
Stiamo calcolando ΔSuniv da sole informazioni relative al sistema ma non stiamo però trascurando
l’ambiente perchè il suo cambiamento di entropia è espresso mediante proprietà del sistema
Moltiplicando per -T cambia il segno di diseguaglianza
-TΔSuniv = -TΔSsist + ΔHsist < 0
-TΔSuniv = ΔH - TΔS
Il prodotto -T • S = G
La quantità -T • ΔSuniv = ΔG
ENERGIA LIBERA DI GIBBS
VARIAZIONE DI ENERGIA LIBERA
Δ G = Δ H - TΔ S < 0
È LA PIÙ IMPORTANTE EQUAZIONE DELLA TERMODINAMICA
SPONTANEITÀ
1)
2)
3)
4)
Poichè H e S sono funzioni di stato, anche G è una funzione di stato.
La variazione di G (ΔG) fissa la direzione di un processo spontaneo in funzione delle proprietà del
solo sistema.
La relazione - T • ΔSuniv = ΔG garantisce che se ΔSuniv > 0 (processo spontaneo), risulta sempre
ΔG < 0: un processo è spontaneo quando ΔG < 0.
Energia libera significa libera di essere disordinata, capace di causare cambiamento, capace di
fare lavoro:
ΔG
Energia
libera
5)
=
ΔH
-
Energia
totale
TΔS
Energia già
disordinata
ΔG è una misura della competizione tra l’effetto energetico (ΔH) e l’effetto probabilistico (ΔS),
ovvero tra la tendenza dell’energia ad assestarsi su valori minimi e dell’entropia ad assestarsi su
valori massimi.
ΔG = Gfinale – Giniziale = Gprodotti - Greagenti
Epot
Sistemi
meccanici
ΔEpot < 0
G
GREAG
ΔG° < 0
Sistema
chimico
ΔG < 0
G
ΔG = 0
GREAG
=
G
GPROD
GPROD
ΔG > 0
GPROD
a)
A
B
spontaneo
GREAG
b)
A
B
equilibrio
c)
A
B
spontaneo INVERSO
SPONTANEITÀ
ΔG = ΔH - TΔS
La spontaneità di una reazione in termini di ΔG dipende dal segno e grandezza di ΔH e ΔS e da T
ΔS°
ΔH° > 0
ΔH° < 0
ΔG° < 0 sempre
ΔS° > 0
ΔS° > 0
2 N2O (g)
2 N2 (g) + O2 (g)
SPONTANEA A QUALSIASI TEMPERATURA
CaCO3 (s)
SPONTANEA AD ALTE TEMPERATURE
ΔH° < 0
ΔS° < 0
ΔH° > 0
ΔS° < 0
SO2 (g) + ½ O2
SO3 (g)
SPONTANEA A BASSE TEMPERATURE
abcde-
CaO (s) + CO2 (g)
ΔG° > 0 sempre
N2 (g) + 2 O2 (g)
ΔH°
2 NO2 (g)
MAI SPONTANEA
ENERGIA LIBERA MOLARE STANDARD DI FORMAZIONE (ΔG°f)
Stesse considerazioni fatte per ΔH°f
Stato standard di riferimento: una mole di sostanza nel suo stato stabile 1 atm e 25°C
Zero arbitrario: Energia libera molare standard degli elementi uguale a 0 (G°f (elementi) = 0)
Poichè formare 1 mole di elementi ad 1 atm e 25°C a partire da 1 mole di elementi a 1 atm e 25°C
non comporta variazione di energia libera: ΔG°f (elementi) = 0
ΔG°f (composto) = variazione di G associata alla formazione di una mole di composto a partire dagli
elementi che lo costituiscono (tutti nelle condizioni standard)
CH4 (g)
a 25°C e 1 atm
ΔG°f = - 50,8 kJ/mol
Cgraf + 2 H2 (g)
ΔH°f (elementi) = 0
ΔG°f (elementi) = 0
S°f (elementi) ≠ 0
ΔH°f (composti)
ΔG°f (comosti)
S°f (elementi) e S°f (elementi)
TABULATI (kJ/mol)
TABULATI (kJ/mol)
TABULATI (J/K)
J/K
ATTENZIONE
ΔG° - STABILITÀ TERMODINAMICA
ΔG°f (composto) è una misura della stabilità termodinamica del composto nei confronti degli elementi che lo
costituiscono:
ΔG°f (composto) < 0
elementi
ΔG°f (composto) > 0
composto
formazione
composto (spontaneamente)
elementi (spontaneamente)
A MENO CHE IL COMPOSTO NON SIA CINETICAMENTE STABILE
⇒ Cgraf
Cdiam
ΔG°f = + 2,9 kJ/mol
Il Cdiamante è TERMODINAMICAMENTE INSTABILE (tenderebbe a
CINETICAMENTE STABILE (ossia decompone MOLTO LENTAMENTE).
convertirsi
in
grafite)
ma
SOLO LA CINETICA CI PERMETTE DI DIRE “UN DIAMANTE È PER SEMPRE”
Allo stesso modo il BENZENE (ΔG°f = + 124,3 kJ/mol) si conserva in bottiglia senza decomporsi
(CINETICAMENTE STABILE)
ENERGIA LIBERA STANDARD DI REAZIONE (ΔG°reaz)
Il calcolo dipende da T (ΔG°reaz = f(T) : A) T = 298 K; B) T ≠ 298 K
Caso in cui T = 25°C: si calcola a partire dai ΔG°f (PERCHÈ SONO TABULATI A 25°C)
ΔG°reaz (298 K) = ∑ ΔG°f (prodotti
(prodotti)) - ∑ ΔG°f (reagenti
(reagenti))
CaO (s) + CO2 (g)
(T = 298 K)
Es: CaCO3 (s)
ΔG°reaz = [ΔG°f (CO2 (g)) + ΔG°f (CaO (s))] – [ΔG°f (CaCO3 (s))] =
[(-394,4 kJ/mol) + (-604 kJ/mol] – (-1129 kJ/mol)] = 130,2 kJ > 0
ΔG°reaz = ΔH°reaz - TΔS°reaz
(T = 298 K)
la reazione a 25°C e 1 atm
NON È SPONTANEA
porta allo stesso risultato
Caso in cui T ≠ 25°C: ΔG°reaz (T) varia molto con la temperatura. Si calcola usando l’equazione
ΔG°reaz (T) = ΔH°reaz - TΔS°reaz
in prima approssimazione i valori ΔH°f e S° (tabulati a 25°C) li riteniamo indipendenti da T (uguali a
qualsiasi T), ma le reazioni non spontanee a 25°C possono diventarlo a T ≠ 25°C, in funzione del segno
di ΔH°reaz e ΔS°reaz
Es: CaCO3(s)
CaO(s) + CO2(g)
(T = 298 K)
ΔG°reaz (1200 K) = ΔH°reaz (298 K) – 1200 K ·ΔS°(298 K) = 178,3 kJ – 1200 K·158,9·10-3 kJ/K = -13 kJ < 0
ΔH° > 0
ΔS° > 0
ENDOTERMICA
DISORDINANTE
(l’amb. si ordina)
(il sistema si disordina)
⇒ La decomposizione di CaCO3 è spontanea a 1200 K ma non lo è a 298 K
Essendo una reazione endotermica è favorita ad alte temperature in quanto il prelievo di Etermica
dall’ambiente caldo provoca un minore ordine di movimento nell’ambiente stesso.
La TEMPERATURA MINIMA al di sopra della quale la reazione (in condizioni standard ≡ reagenti e
prodotti a P 1 atm.) diventa spontanea è la TEMPERATURA DI EQUILIBRIO IN CONDIZIONI STANDARD.
Calcoliamola:
All’equilibrio:
ΔG°(T)
ΔH°
ΔG°(T) = 0
ΔG°(T) = 0 ⇒
ΔG°(T) = ΔH° -TΔS° = 0
⇒
Equazione di una retta
T = ΔH°/ΔS°
Intercetta ascisse
Es: Calcolare a che temperatura la decomposizione del
CaCO3 è in equilibrio in condizioni standard (ΔG°T = 0)
CaCO3(s)
0 (K)
CaO(s) + CO2(g)
T (K) T = ΔH°/ΔS° = 178,3 kJ/(158,9x10-3 kJ) = 1128 K
T equilibrio in condizioni standard: ΔG°(T) = 0
T = 1128 K
Quindi: per ogni reazione esiste una temperatura a cui reagenti e prodotti sono in equilibrio nel loro
STATO STANDARD (ΔG°T = 0 e Kp = 1 perchè tutte le p parziali sono = 1 atm) ⇒
EQUILIBRIO
CaCO3 (s)
T = 855 °C
(1 atm)
CaO (s) + CO2 (g)
(1 atm)
(1 atm)
Nella decomposizione di CaCO3 a 855°C si forma CO2 ad 1 atm. La pressione di CO2 all’interno del
recipiente scaldato a 855°C ha il valore di 1 atmosfera.
EQUILIBRIO
H2O(l)
H2O(g)
ΔG°25°C = ΔG°f (H2O(g)) - ΔG°f (H2O (l)) = 8,6 kJ > 0.
Quando T = 25°C
ΔG°(T)
ΔH°
ΔG°(T) = 0
Quindi a 25°C non si formerà H2O (g) ad 1 atm in un recipiente
chiuso. Avverrà invece la trasformazione contraria.
T = 100 °C
0 (K)
T (K)
Ma per T = ΔH°/ΔS° = 373 K = 100°C H2O
equilibrio con il loro stato standard.
(l)
e H2O
(g)
sono in
CRITERIO QUALITATIVO PER VALUTARE SE UN PROCESSO È SPONTANEO IN COND. STANDARD
ΔG°(T)
ΔG°(T)
Esotermica: ΔH° < 0
Disordinante: ΔS° > 0 0 (K)
Esotermica: ΔH° < 0
Ordinante: ΔS° < 0
0 (K)
sempre spontaneo
T (K)
ΔH°
spontaneo a basse T
ΔG°(T) < 0
ΔG°(T)
Endotermica: ΔH° > 0 ΔH°
Disordinante: ΔS° > 0
Teq
Endotermica: ΔH° > 0
Ordinante: ΔS° < 0
0 (K)
T (K)
ΔG°(T) < 0 per T > Teq
T (K)
ΔH°
ΔG°(T) < 0 per T < Teq
ΔG°(T)
Kp = 1
spontaneo ad alte T
Teq Kp = 1
mai spontaneo
ΔH°
0 (K)
ΔG°(T) > 0 sempre
T (K)
ENERGIA LIBERA (ΔGreaz) E LAVORO UTILE (Lutile)
ΔGreaz = Lutile : massima quantità di energia che può essere trasformata in lavoro utile (a P e T cost)
ΔGreaz = Lmax ottenibile
Processo spontaneo ⇒ ΔGreaz < 0 (ΔSuniv > 0): lavoro fatto dal sistema sull’ambiente (-L)
Il lavoro (-L) rappresenta la massima quantità di lavoro ottenibile da una trasformazione spontanea ed
eguaglia esattamente la diminuzione di energia libera.
Processo non spontaneo ⇒ ΔGreaz > 0 (ΔSuniv < 0): lavoro dall’ambiente sul sistema (+L)
Il lavoro (+L) rappresenta la minima quantità di lavoro ottenibile da fare perchè avvenga una
trasformazione non spontanea ed eguaglia esattamente l’incremento di energia libera.
RENDIMENTO (η%) DI UNA REAZIONE
ΔGreaz (T) =
ΔHreaz -
TΔSreaz
Energia libera
per compiere
lavoro
Energia
totale
disponibile
Energia già
disordinata
ΔHreaz =
ΔGreaz (T) +
TΔSreaz
Energia
totale
disponibile
Energia
utilizzabile per
compiere
lavoro
Energia già
utilizzata
η% = (Eutilizzabile / Etotale) x 100 = (ΔGreaz / ΔHreaz) x 100