entropia-en.libera

SECONDO PRINCIPIO DELLA TERMODINAMICA E ENTROPIA
SPONTANEITA’
Una trasformazione si dice SPONTANEA quando avviene naturalmente senza alcuna azione
esterna: il trasferimento di calore da un corpo più caldo ad un corpo più freddo, l’espansione di un
gas nel vuoto, lo scioglimento di un cubetto di ghiaccio in acqua…. Questi fenomeni spontanei non
possono avvenire al contrario.
Il raffreddamento dell’acqua calda fino a temperatura ambiente è un esempio di trasformazione
fisica spontanea; la trasformazione inversa non può avvenire spontaneamente. Per riscaldare
l’acqua, come si sa, dobbiamo metterla in una pentola e porla sopra una fiamma. Anche le carte da
gioco si dispongono spontaneamente in disordine, rimetterle in ordine è un’operazione che avviene
solo con l’intervento dell’uomo.
Molte reazioni spontanee sono accompagnate da una diminuzione di entalpia ma questo non è
l’unico fattore che ci permette di individuare una reazione spontanea; diciamo che è vero che molte
reazioni spontanee comportano uno sviluppo di calore ma esistono anche reazioni endotermiche che
avvengono spontaneamente pur avendo prodotti con energia maggiore dei reagenti.
Quindi il criterio termico non funziona sempre; infatti il primo principio ci dice che l’energia di una
trasformazione si conserva ma non si occupa del perché una reazione proceda in un senso piuttosto
che in un altro.
E’ evidente che intorno a noi accadono fenomeni naturali che hanno una direzione preferenziale
e lasciano un segno indelebile nell’universo cioè lo modificano irreversibilmente.
Uno degli enunciati del secondo principio è:
“Quando nell’Universo si realizza un evento spontaneo si ha sempre un aumento
di entropia”
Il secondo principio completa il primo il quale prende in considerazione l’energia solo dal punto
di vista quantitativo affermando che in un sistema isolato la quantità totale di energia si conserva
mentre il secondo sostiene che l’energia possiede anche una qualità e che nei processi di
trasformazione l’energia tende spontaneamente a degradarsi passando gradualmente da forme più
pregiate a forme meno pregiate. Il calore non è una forma pregiata di energia mentre lo è ad
esempio l’energia meccanica o quella elettrica che sono in grado di produrre lavoro con rendimenti
elevati. In realtà anche per quanto riguarda il calore esistono diversi gradi di qualità nel senso che
questa forma di energia è più pregiata quando conferisce ai corpi una temperatura più elevata: in
questo caso possiede infatti una maggiore capacità di produrre lavoro. Il ferro da stiro deve essere
ben caldo per eliminare le pieghettature presenti nelle camicie dopo che sono state lavate. Quando
lo si lascia raffreddare si assiste ad un fenomeno spontaneo e irreversibile con degradazione
dell’energia che finisce nell’ambiente e quel prezioso elettrodomestico a temperatura ambiente non
è più in grado di produrre il lavoro di stiratura delle camicie.
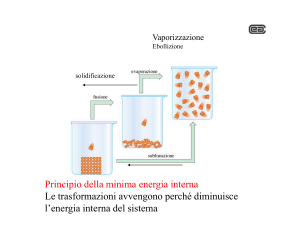
Ci sono anche processi reversibili nel tempo cioè all’equilibrio, (passaggi di stato per esempio) che
avvengono attraverso una successione di stati vicini tra loro.
“Si definisce processo reversibile quello che può avvenire in entrambe i sensi rispetto al tempo,
senza che questo comporti un cambiamento sostanziale nell’ambiente”
L’ENTROPIA
Si osserva anche che in un sistema isolato avvengono spontaneamente quelle trasformazioni che
comportano un aumento del DISORDINE : per esempio nel trasferimento di calore da un corpo più
caldo ad uno più freddo il sistema isolato ha ridistribuito la propria energia fra un numero maggiore
di particelle che avranno una maggiore energia cinetica .
La funzione di stato che esprime il disordine di un sistema è l’ENTROPIA S e L.Boltzmann (fisico
austriaco) alla fine del 1800 individuò una relazione matematica tra S e il grado di disordine
S = k lnW
k = costante di Boltzmann 1,3806 x 10-23 J/K
W = numero di modi diversi in cui gli atomi possono disporsi in un sistema
numero di microstati in cui si può configurare il sistema
Qui il termine disordine va messo in relazione con il termine molteplicità e la direzione spontanea
di un processo con la tendenza a realizzare lo stato più probabile.
D’altra parte anche dal punto di vista statistico uno stato disordinato è molto più probabile di uno
stato ordinato perché il primo ha più modi per essere realizzato.
Per illustrare il concetto consideriamo allora un mazzo di carte nuovo il quale, come tutti sanno, è
ordinato per seme e valore crescente della carta; mescolandolo è praticamente nulla la probabilità
che si possa ritornare all’ordine iniziale. Ciò dipende dal fatto che a fronte di un solo stato di ordine
vi sono miliardi di miliardi di miliardi… (1052) di stati di disordine possibili. In generale gli stati di
disordine sono infinitamente maggiori di quelli, anzi nel nostro caso dell’unico, di ordine.
ENTROPIA E CALORE
Matematicamente l’entropia si può calcolare dalla relazione
S = Q / T
(J/K)
La variazione di entropia dipende anche dalla temperatura : infatti se una sostanza assorbe calore la
velocità delle sue molecole aumenta, di conseguenza il disordine.
Ma l’effetto sul disordine si fa sentire meno quando ho già raggiunto temperature elevate.
Abbiamo visto che il disordine aumenta con l’aumentare della temperatura. Per esempio, alla
temperatura di 100 °C e alla pressione di un’atmosfera l’acqua passa dallo stato liquido a quello
aeriforme che è uno stato della materia altamente disordinato. Se il vapore acqueo lo si chiude in un
recipiente e si abbassa la temperatura esso condensa e si forma un liquido nel quale il disordine
sussiste ancora ma è molto minore di prima. Se si raffredda l’acqua liquida diminuisce
ulteriormente il disordine perché le molecole diventano sempre più lente fino a che, alla
temperatura di zero gradi centigradi, il liquido solidifica e diventa ghiaccio. Il ghiaccio è un solido
cristallino in cui le molecole si trovano in uno stato altamente ordinato e l’entropia del sistema è
molto bassa tuttavia ogni molecola ha ancora energia cinetica sufficiente per vibrare intorno alla sua
posizione di equilibrio.
Quando alla fine si porta il sistema allo zero assoluto ( 273°C sotto lo zero) il ghiaccio si troverà in
uno stato di ordine perfetto ed ogni possibile attività cesserà. Questa osservazione porta
all’enunciato di quello che in modo improprio viene chiamato il “terzo principio della
termodinamica” il quale afferma che allo zero assoluto (T = 0 K) l’entropia di un cristallo puro è
pari a zero (S = 0).
Per i diversi composti è stata misurata l’entropia molare standard S° che rappresenta l’entropia di
una sostanza allo stato puro, alla p= 1 atm, a 25°C; L’unità di misura : Joule / K mol
Chiaramente S° = 0 per un cristallo puro allo zero assoluto.
In un sistema chiuso (es. reazione chimica) conoscendo i valori di S° posso calcolarmi S° reagenti,
S° prodotti e quindi S° reazione.
ENERGIA LIBERA E SPONTANEITA’ DELLE REAZIONI
In realtà non sempre in una trasformazione aumenta l’entropia nel sistema in esame: i processi
metabolici cioè quelli che avvengono all’interno delle cellule invece che creare disordine
aumentano l’ordine (la grandezza fisica che viene detta “neghentropia”). Questa circostanza si
verifica ad esempio nella fotosintesi in cui si formano molecole complesse e ordinate (composti
organici) utilizzando molecole semplici e poco organizzate (acqua e anidride carbonica). Sebbene
questi processi diminuiscano l’entropia della cellula, l’entropia all’esterno di essa aumenta ed
aumenta in misura tale da compensare abbondantemente l’ordine che si è venuto a creare all’interno
della cellula stessa. Ciò è conseguenza del fatto che la cellula è un sistema aperto nel quale sono
possibili scambi di materia e di energia con l’ambiente esterno. A questo punto è opportuno chiarire
la variazione di entropia in un sistema chiuso.
Consideriamo un sistema chiuso in cui avvenga una reazione chimica e che scambi solo energia con
l’ambiente.
Se la reazione avviene spontaneamente deve essere
Ssist + Samb = Suniv > 0
Come faccio a calcolare la variazione in tutto l’ambiente circostante? Non è possibile con la
formula di Boltzmann ma dovrò considerare il calore che si è sviluppato nella trasformazione.
Se la reazione è esotermica per esempio l’aumento di entropia dell’ambiente è direttamente
proporzionale al calore ceduto dal sistema e inversamente proporzionale alla temperatura cioè
Qs = Hsist<0
e più precisamente
Samb =- Qsist/T = - Hsist/ T>0
Per una reazione endotermica si ottiene una relazione con il segno contrario.
La variazione complessiva di entropia sarà data da :
Suniv = Ssist + Samb = Ssist - Hsist/T>0
TSuniv = TSsist - Hsist > 0
Hsist - TSsist < 0
Mi posso concentrare completamente sulla trasformazione che avviene nel sistema e che posso
controllare più facilmente
E’ opportuno a questo punto definire una nuova funzione di stato che mi permetta di prevedere la
spontaneità di un processo tenendo conto sia dell’entalpia che dell’entropia
ENERGIA LIBERA G
G= H -TS
A temperatura e pressione costanti
G = H - TS
(alla variazione di entalpia devo togliere quella parte di energia che va ad aumentare il disordine).
L’energia “libera” corrisponde all’energia totale resa disponibile dal comportamento spontaneo del
sistema e utilizzabile come lavoro “utile”.
STUDIO DEL SEGNO DI G
H
<0
<0
>0
>0
S
>0
<0
>0
<0
G
<0
<0
<0
>0
REAZIONE SPONTANEA
SEMPRE
Solo se H>TS a bassa T
Solo se H<TS ad alta T
MAI
Per una qualsiasi reazione posso calcolarmi il valore di G°reaz = G°prod - G°reag
Conoscendo i valori di G° di formazione dei singoli composti.
Oppure
G°reaz= H°reaz - TS°reaz
a T costante
EQUILIBRIO CHIMICO
Quando G = 0 il sistema è all’equilibrio (reazione reversibile).
Sapendo che
G = G° + RT ln Q
(equazione di Van’t Hoff)
All’equilibrio G° = - RTln Keq
Se
R = 8,314 J/K mol
G° = 0
Keq = 1
G° < 0
Keq > 1
reazione va verso destra per raggiungere l’equilibrio
G° > 0
Keq < 1
reazione va verso sinistra per raggiungere l’equilibrio
Si può anche ricavare il valore di Keq :
G°/ RT = -ln K
log K =-G° / 2,3 RT
K = 10 - G°/2,3 RT