Un secondo libro di riferimento

Giuseppe Santucci
Qualità nella Produzione del Software
05
Fondamenti della teoria della misura
&
elementi di statistica
descrittiva ed inferenziale
05FTM.1
QPsw
Un secondo libro di riferimento
• Metrics and Models In Software Quality Engineering - Second Edtion
• Stephen H.Kan
• Addison Wesley - 2003
QPsw
05FTM.2
Perchè si misura ?
•
•
“Non puoi controllare ciò che non puoi misurare” [T. De Marco, 1982]
Le misure, nel campo della qualità del sw, si effettuano per i seguenti
obbiettivi:
1. verificare l'aderenza di alcuni parametri (di qualità) a dei valori di
riferimento (esterni/interni)
2. rilevare delle deviazioni relative alla pianificazione temporale/
allocazione di risorse
3. raccogliere indici di produttività
4. validare l'effetto di strategie tese a migliorare un processo produttivo
(qualità/ produttività / aderenza alla pianificazione / controllo dei costi)
•
In sintesi si misura per controllare e prendere decisioni
05FTM.3
QPsw
Pragmaticamente
Misura e analisi
dei dati
QPsw
05FTM.4
Processo di misura
Rating (definizione dei livelli di riferimento)
Le metriche forniscono valori quantitativi che non sono di per sé una valutazione della qualità, dobbiamo
mappare i dati quantitativi su una scala qualitativa
A carico dell’
organizzazione
QPsw
Analisi statistica dei dati
05FTM.5
Definizioni, Definizioni operative e misure...
• Prima di entrare nel merito delle varie misure e dei livelli di riferimento è
opportuno richiamare alcune nozioni di base della Teoria della Misura,
spesso confuse o ignorate
• Utilizzeremo un esempio, basato sulla seguente proposizione:
“più è rigorosa la parte finale del processo di produzione del sw più è alta la
qualità del sw presso il cliente”
• per poter accettare/respingere l'affermazione abbiamo bisogno di definire
meglio alcuni concetti:
– processo di produzione: <raccolta requisiti, progetto, ... ,integrazione, ...
,test di accettazione>
– parte finale del processo di produzione: <integrazione con il relativo test>
(dopo le modifiche sono fortemente controllate)
QPsw
05FTM.6
...Definizioni, Definizioni operative e misure...
• rigoroso: <aderente alla documentazione dei processi (manuale qualità)> ma
è ancora vago ed abbiamo bisogno di alcuni indicatori:
– ad esempio, se è prevista una ispezione del codice; una definizione operativa
potrebbe essere relativa alla percentuale di codice effettivamente ispezionato
– relativamente alla qualità di una ispezione potremmo utilizzare operativamente
una scala di Likert a 5 valori (1=ispezione di bassa qualità ... 5=veramente
efficace)
– la rigorosità del test potrebbe essere operativamente associata alla
percentuale di linee di codice testate e la sua efficacia al numero di difetti
rimossi per KLOC
• qualità del sw presso il cliente: <il numero di errori per KLOC trovati
durante il test di sistema>
• N.B. le definizioni utilizzate sono opinabili, ma non ambigue e misurabili
QPsw
05FTM.7
...Definizioni, Definizioni operative e misure...
Ora è possibile riformulare la proposizione di prima tramite le seguenti
tre ipotesi:
1. maggiore è la percentuale di linee di codice testate minore è il
numero di errori per KLOC trovati durante il test di sistema
2. maggiore è l'efficacia delle ispezioni minore è il numero di errori per
KLOC trovati durante il test di sistema
3. maggiore è l'efficacia del test, in termini di errori trovati, minore è il
numero di errori per KLOC trovati durante il test di sistema
QPsw
05FTM.8
...Definizioni, Definizioni operative e misure
• L'esempio porta a capire l'importanza delle misure nonchè la necessità
di vari livelli di astrazione:
Teoria
Concetti
Mondo astratto
Proposizioni
Definizioni
Ipotesi
Definizioni operative
Analisi dei dati
Misure
Mondo empirico
05FTM.9
QPsw
• Teoria
– un insieme di PROPOSIZIONI relative a CONCETTI
• Proposizione
– viene fromalizzata tramite delle DEFINIZIONI
– da luogo ad una o più IPOTESI empiriche
• Ipotesi
– per essere validata necessita di misure, fromalizzate tramite
DEFINIZIONI OPERATIVE
• Analisi dei dati
– parte finale del processo, teso a validare la teoria. Si sostanzia
effettuando delle MISURE nel mondo reale
QPsw
05FTM.10
...Definizioni, Definizioni operative e misure...
• Per validare la teoria è necessario (a) introdurre l'unità di analisi (componente o
progetto), (b) effettuare analisi statistiche per validare le ipotesi (e.g., analisi della
varianza), (c) validare gli indicatori scelti, ovvero effettuare ed interpretare delle
misure
• Ad esempio, volendo validare la teoria tramite l’ipotesi 1),assumiamo di aver
ottenuto le seguenti misure tramite una unità di analisi composta da 9
esperimenti (3 al 50%, 3 al 70%, 3 al 90%) :
• Percentuale linee di codice testate
Errori trovati durante il test di sistema
50%
20/KLOC
70%
15/KLOC
90%
12/KLOC
• Senza una corretta analisi dei dati (quale l'analisi della varianza, ANOVA) non
potremmo essere sicuri della significatività statistica di quanto ottenuto
• Ad esempio se 20 è la media di {19 20 21}, 15 di {15 15 15}, e 12 di {11 12 13} ci
sentiremmo abbastanza sicuri
• Se invece 20 è la media di {5 5 50}, 15 di {1 4 40} e 12 di {3 3 30}...
• Vedremo la cosa successivamente
05FTM.11
QPsw
Elementi di base della teoria della
misura
QPsw
05FTM.12
Terminologia base (1/3)
• Misura
– Variabile cui viene assegnato un valore a seguito di una misurazione
• Misura base
– Una misura funzionalmente indipendente da altre
• Misura derivata
– Una trasformazione di una misura base effettuata utilizzando una
funzione matematica
• Indicatore
– Misura che può essere usata per stimare o prevedere un’altra misura
05FTM.13
QPsw
Terminologia base (2/3)
• Metodo di misurazione
– Sequenza logica di operazioni effettuate per assegnare un valore
quantitativo ad una variabile che descrive un attributo, rispetto ad una
scala di riferimento
• Metodo di valutazione
– Una procedura che descrive le azioni da compiere al fine di utilizzare
delle misure per esprimere un giudizio
• Validazione
– Conferma, attraverso la presentazione di una evidenza oggettiva, che
un requisito è stato rispettato nel prodotto
– La validazione può riguardare output della fase di progettazione (ad es.
disegni tecnici, schemi di basi di dati) così come della fase di sviluppo
(ad es. codice sorgente, manuali d’uso), in vari stadi di lavorazione
QPsw
05FTM.14
Terminologia base (3/3)
• Verifica
– Conferma, attraverso la presentazione di una evidenza oggettiva, che
una attività è eseguita correttamente
• Rating
– Metodo per mappare un valore misurato su una scala di valutazione
(ad es. “tempo di risposta” < 1 sec = “buono”)
• Scala di misura
– Un insieme ordinato di valori, continui o discreti, od un insieme di
categorie, rispetto ai quali è mappato un attributo
05FTM.15
QPsw
Definizione di scala di misura
• Si definisce scala di misura l’insieme di:
– un sistema di relazioni empiriche S
• A è più alto di B
– un sistema di relazioni numeriche R
• 180 cm > 160 cm
– un mapping tra S ed R
• A è più alto di B di 20 cm
– Poiché il numero di possibili insiemi di relazioni empiriche e numeriche
è pressoché infinito, infinite sono le scale di misura utilizzabili
– Nella pratica
•
•
•
•
•
QPsw
Nominale
Ordinale
Intervalli
Razionale
Assoluta
05FTM.16
Scale di una misura(1)
• Scala Nominale - Insieme predefinito non ordinato di valori distinti
– esempio: possibili tipi di errori di programmazione (di sintassi, semantici
etc. senza definire una gerarchia di gravità degli errori)
– operatori ammisibili { = , !=}
– Se si utilizza questo tipo di scala, calcolare valori medi ha significato
solo se si vuole verificare la frequenza con cui certe misure si
collocano in date classi. Altre operazioni tra le misure non hanno
significato
05FTM.17
QPsw
Scale di una misura(2)
• Scala Ordinale - Insieme predefinito ordinato (ordinamento totale) di valori
distinti
– esempio: livelli CMM
– operatori ammissibili { = , !=, >, < }
– N.B. NON è possibile confrontare l'entità delle differenze: il livello 3 CMM è
maggiore del livello 2 ma non è noto DI QUANTO
– N.B. NON è possibile fare paragoni: non è possibile dire che la differenza
tra 1 e 2 è la stessa che esiste tra 3 e 4
– In alcuni casi (scale di Likert) è assunta l'ipotesi di equidistanza per fare la
media tra valori differenti. ATTENZIONE alle conseguenze:
• Scala di Likert a 5 valori sui risultati di una nuova terapia sperimentale: (1-guarito
perfettamente , 2-complicazioni lievi, 3-complicazioni medie, 4-complicazioni
gravi, 5-morto)
– 50 guariti perfettamente e 50 morti ---> complicazioni medie...
– Se si utilizza questo tipo di scala, calcolare la mediana ha significato solo se
si vuole verificare la frequenza con cui certe misure si collocano in date
classi. Altre operazioni possibili sono la determinazione di "maggiore di" o
"minore di", l’uguaglianza, il calcolo dei percentili
QPsw
05FTM.18
Scala di una misura(3)
• Scala per Intervalli - In questo caso è nota la differenza esatta tra due
valori
–
–
–
–
–
esempio: temperatura in gradi (C o F)
richiede una definizione PRECISA dell'unità di misura adoperata
valori interi o reali
operatori ammissibili { = , !=, < , >, +, - }
N.B. La presenza di uno zero arbitrario NON autorizza a fare ipotesi di
rapporti: posso dire che tra 80°F e 20° F ci sono 60° di differenza, NON
che 80°F è 4 volte più caldo di 20°F
– Possono essere fatti confronti (=, !=, >, <) operazioni di addizione e
sottrazione tra le misure. Si possono calcolare la media aritmetica, la
deviazione standard.
05FTM.19
QPsw
Scala di una misura(4)
• Scala Razionale o a rapporti - Scala per intervalli in cui è definito in
modo non arbitrario uno zero
– esempio: temperatura in gradi Kelvin (zero assoluto!)
– operatori ammissibili { = , !=, < , >, +, -, x, /}
– 90°K è 3 volte maggiore di 30°K
• Tranne pochi casi, tutte le scale per intervalli sono scale razionali
• Si possono effettuare confronti, addizioni, sottrazioni, moltiplicazioni e
divisioni tra misure. Si possono calcolare la media armonica e
geometrica, la variazione percentuale, l'indice di correlazione.
• Ovviamente valgono le seguenti relazioni ISA:
• S. Razionale -> S. Intervalli -> S. Ordinale-> S. Nominale
• Scala Assoluta - In questa scala si contano le occorrenze effettive
delle entità.
– Ad esempio, le LOC che costituiscono un programma.
QPsw
05FTM.20
Scelta della scala di misura
• La scelta della scala dipende dall'attributo che si vuole misurare. La
scala scelta deve corrispondere ad un effettivo sistema di relazioni
valido per l'attributo. I valori numerici associati alle misurazioni
dell’attributo devono corrispondere ad effettive relazioni empiriche fra
le entità misurate
• Ad esempio, se per un determinato prodotto non è possibile stabilire
che è "affidabile" in maniera esattamente doppia o tripla etc.. di un
altro, non ha senso utilizzare una scala diversa da quella nominale od
ordinale
05FTM.21
QPsw
Sinottico scale di misura (1)
TIPO DI
SCALA
TRASFORMAZIONI
AMMISSIBILI
NOMINALE
qualsiasi
determinazione di
trasformazione unouguaglianza
a-uno
ORDINALE
M(x)>M(Y) implica
che M’(x)>M’(Y)
[funzione crescente
strettamente
monotona]
M’=aM+n(a>0)
INTERVALLARE [trasformata lineare
positiva]
RATIO
(DI RAPPORTI)
ASSOLUTA
QPsw
OPERAZIONI
EMPIRICHE DI
BASE
M’=aM (a>0)
[trasformazione di
similarità]
M’=M
[identità]
ALCUNI INDICI
STATISTICI
APPROPRIATI
TEST
STATISTICI
APPROPRIATI
ESEMPI
Moda
Frequenza
non parametrico
etichettare
classificare entità
come la
precedente, più la
determinazione di
“maggiore di” e
“minore di”
Mediana
Percentili
Spearman r
Kendall W
Kendall T
non parametrico
preferenza
ordinamento di entità
come la
precedente, più
addizioni e
sottrazioni
Media Aritmetica
Deviazione standard
non parametrico
Correlazione Pearson
Correlazione multipla
temperature in gradi
Fahrenheit o Celsius
date di calendario
orario
come la
precedente, più
moltiplicazioni e
divisioni
Media Geometrica
Media Armonica
Coefficiente di
variazione
Variazione
percentuale
Indice di correlazione
intervalli di tempo
non parametrico
temperature Kelvin
e parametrico
lunghezze
conteggio di entità
05FTM.22
Sinottico scale di misura (2)
05FTM.23
QPsw
Tipi di misura
QPsw
05FTM.24
Tipi di misura: rapporti e proporzioni
• Rapporto - Risultato di una divisione tra due valori che vengono da due
dominii distinti e mutuamente esclusivi. Il risultato della divisione è
moltiplicato per 100
– esempio: (numero maschi/numero femmine) x 100
– può assumere valori sotto e sopra il 100
– esempio sw: linee di commento/linee di codice
• Proporzione - Risultato di una divisione tra due valori in cui il dividendo
contribuisce al valore del divisore, e.g., a/(a+b)
– esempio: numero utenti soddisfatti/numero utenti
– assume valori compresi tra 0 ed 1
– spesso il denominatore è composto da vari elementi per i quali si
calcolano le varie proporzioni:
• a+b+c=N ; a/N + b/N + c/N =1
– una Frazione è una proporzione tra reali
05FTM.25
QPsw
Tipi di misura: percentuale
• Percentuale - Una proporzione o frazione espressa normalizzando il
denominatore a 100.
– esempio: i difetti presenti nei requisiti erano il 15%, nel progetto il 25%,
nella codifica il 60%
– la percentuale va usata con criterio, indicando i valori coinvolti ed
evitandone l'uso quando gli elementi sono meno di 30-50 (da la falsa
impressione di una grossa quantità di dati)
– esempio: dei difetti presenti nel progetto il 25% era nei requisiti, il 15%
nel progetto ed il 60% nella codifica
– esempio: i difetti presenti nel progetto erano 20, di cui 5 nei requisiti, 3
nel progetto e 12 nella codifica
QPsw
05FTM.26
Tipi di misura: andamento
•
•
Andamento (rate) - Indica, al contrario di rapporti, proporzioni e percentuali,
un valore associato alla dinamica di un fenomeno. Tipicamente (ma non
sempre) è la misura del cambiamento di una quantità (y) rispetto all'unità di
un'altra quantità (x) da cui dipende. Quasi sempre x è il tempo.
esempio: negli studi demografici si parla andamento approssimato (crude)
delle nascite in un certo anno calcolandolo con la seguente formula:
(N/P)*k
N=nascite nell'anno osservato
P= popolazione (calcolata a metà dell'anno)
k=costante, tipicamente 1000
05FTM.27
QPsw
Tipi di misura: andamento
• è presente il concetto di "esposizione al rischio", ovvero il fatto che gli elementi del
denominatore possono "diventare" o "produrre" elementi nel numeratore
• considerando tale fattore, la formula di prima può essere migliorata sostituendo a
P P' il numero delle donne tra i 15 e 44 anni (andamento della fertilità):
(N/P')*k
• andamento dei difetti=(D/OFE) *k dove
– D=difetti osservati nel periodo di rifermento e
– OFE =Opportunities For Error: possibili punti in cui possono essere "generati" errori
• esempio sw: andamento dei difetti: (D/KLOC)* 1000 dove
•
D=difetti osservati nel periodo di rifermento (anno, mese)
• N.B. è un andamento "crude" perchè le KLOC non concidono direttamente con le
OFE in quanto a volte un errore coinvolge più linee di codice (o una linea di
codice genera + errori)
QPsw
05FTM.28
Richiami di statistica descrittiva
• Data una popolazione di N elementi noti su cui si effettua una misura (e.g.,
l'età degli studenti di questo corso) {x1,...,xn}, si definiscono i seguenti
parametri:
• media
m= (x1+ x2+... +xn)/N
• varianza var=[(x1-m)2+ (x2-m)2 +...(xn-m)2]/N
• deviazione standard σ=var1/2
• spesso la varianza si indica con σ2
05FTM.29
QPsw
Ulteriore caratterizzazione dei dati raccolti
•
•
•
•
QPsw
Mediana
Moda
Calcolo Percentili (Quartili)
Distribuzione di frequenza
05FTM.30
Calcolo dei percentili
• I percentili sono quegli elementi che dividono una distribuzione
ordinata in parti uguali, ciascuna delle quali contiene l'x per cento della
distribuzione. Se dividiamo la distribuzione ordinata in 10 parti di
uguale numerosità, ciascun elemento (modalità) separatore si
chiamerà decile.
• Il primo decile divide in due parti la distribuzione ed è rappresentato
dall'elemento che lascia alla sua sinistra il 10 per cento delle unità del
collettivo con modalità più piccole o uguali e alla sua destra il 90 per
cento delle unità che presentano modalità più grandi. Il secondo decile
divide la distribuzione in due parti con il 20 per cento e l'80 per cento
rispettivamente, e così via.
05FTM.31
QPsw
Calcolo percentili (quartili)
• I percentili usati più frequentemente sono i quartili che dividono in
quattro parti di uguale ampiezza (quarti) la distribuzione ordinata:
• il primo quartile lascia prima di sé il 25 per cento delle unità che hanno
modalità inferiori e dopo di sé il 75 per cento di unità con modalità
superiori. Si indica con Q1;
• il secondo quartile corrisponde alla mediana e divide la distribuzione in
due parti uguali, lasciando prima di sé il 50 per cento di unità con
modalità più piccole. Può essere indicato, oltre che con Me, anche con
Q2;
• il terzo quartile, Q3, è quella modalità che divide in due parti la
distribuzione ordinata, lasciando prima di sé il 75 per cento delle unità
che presentano modalità inferiori
QPsw
05FTM.32
Mediana (Me) / Moda ( o norma)
• La mediana di una variabile - precedentemente definita come
secondo quartile - è il valore dell’unità che si trova a metà della
distribuzione ordinata, in modo che il 50 per cento dell’insieme
di osservazioni abbia un valore della variabile uguale o inferiore
a esso e il restante 50 per cento un valore superiore.
• Per calcolare la mediana è necessario che la scala utilizzata
variabile sia almeno ordinale.
• Spesso la media e la mediana presentano valori simili. Ciò
accade in particolare quando la distribuzione della variabile è
simmetrica, cioè quando il numero di valori al di sotto del valore
centrale e quelli al di sopra più o meno si equivalgono
• La moda corrisponde al valore della distribuzione che si
presenta più frequentemente
• Una distribuzione si dice unimodale se un solo valore presenta
questa caratteristica, multimodale altrimenti
05FTM.33
QPsw
Distribuzione frequenza
• Si ottiene praticamente ordinando i valori trovati ed indicando, per
ciascuno di essi, la relativa frequenza.
tipicamente gli N elementi si distribuiscono secondo una distribuzione normale
(o gaussiana)
l'analisi delle tecniche di stima della distribuzione di un campione va oltre
gli scopi di questo corso
QPsw
05FTM.34
Distribuzione normale
P
f(x)=ae-(x-b)
μ-1.96σ
μ-σ
μ
μ+σ μ+1.96σ
2/c2
X
68.26% dei dati
95% dei dati
è usuale centrare la gaussiana
sull'asse Y ponendo X=X-m
QPsw
05FTM.35
Alcuni esempi di distribuzione normale
QPsw
05FTM.36
Un indice di qualità stringente: le sei σ
• Nel 1980 la Motorola introdusse uno specifico andamento dei difetti
pari a 3.4 parti difettose su un milione (3.4 ppm), valore che proviene
considerando l'area di una distribuzione normale (gaussiana) calcolata
su una base pari a 12 volte il valore della deviazione standard σ e
tenendo conto delle oscillazioni del processo produttivo pari a 1.5 σ.
0.001 ppm
0.001 ppm
05FTM.37
QPsw
Oscillazioni di 1.5 σ
Ideale
Stringente ma
possibile
QPsw
05FTM.38
le sei σ nel software
•
•
•
Applicata al sw la regola delle 6 σ corrisponde a un andamento dei difetti pari
a 3.4 difetti per milione di linee di codice per l'intero periodo di esercizio del
sw...
Le 6 σ sono nate con l'idea di confrontare più facilmente prodotti ed
organizzazioni. Questa idea può essere contrastata dalle differenti definizioni
operative adottate da varie organizzazioni.
Per il sw:
–
–
QPsw
modo di contare le LOC
linguaggio utilizzato (Motorola propone l'assembler)
05FTM.39
Esercizio sulla caratterizzazione statistica di
un insieme di dati
QPsw
05FTM.40
Grandezze di riferimento
•
•
•
1.
2.
3.
4.
5.
6.
7.
Sia dato un multi-insieme di N valori appartenenti ad una scala
almeno ordinale
Sia x1 .. XN un ordinamento parziale di tali valori
Per caratterizzare i dati in questione occorre calcolare:
la media μ
la deviazione standard σ e la varianza σ2
il valore massimo ed il valore minimo x1 ed xN
la mediana Me (Q2)
il primo ed il terzo quartile Q1 e Q3
la moda
la distribuzione di frequenza
N.B. Tutte queste grandezze sono facilmente calcolabili con Excel
(occorre attivare l'insieme di funzioni statistiche: Tools/Add-ins/AnalysisToolPak)
05FTM.41
QPsw
Media, deviazione standard, varianza e
mediana
• Media deviazione standard e varianza si calcolano banalmente
– μ= (x1+ x2+... +xN)/N
– σ2=[(x1-m)2+ (x2-m)2 +...(xN-m)2]/N
– σ=( σ2)1/2
• Se i dati raccolti sono dispari la mediana corrisponde al numero che
divide a metà l'elenco ordinato dei dati:
– 1 3 7 9 12 25 77 : Me = 9
• Se i dati raccolti sono pari la mediana corrisponde alla media dei due
numeri centrali
– 1 3 7 9 12 25 77 99 : Me = (9+12)/2=10.5
QPsw
05FTM.42
Calcolo del generico percentile
• L’indice del k-esimo percentile è dato da: Ik = (N+1)×k /100
• Dall’indice si ricava quindi il valore esatto con un’interpolazione lineare tra i
due dati (con indici pari all’intero prima e dopo di Ik )
• Esempio N=14 dati. Calcoliamo il 23-esimo precentile
– I23 = (14+1)×23 /100 = 3.45
– Il valore del 23-esimo percentile sarà compreso tra il 3° ed il 4° dato (x3 e x4)
– Numericamente vale x3 + (x4 – x3) × 0.45 (interpolazione lineare)
• Alcuni programmi di calcolo si limitano ad effettuare la media tra i due dati
adiacenti che comprendono il percentile considerato (Matlab). Anche Excel
segue una sua logica personale...
– Con parecchi dati l'approssimazione introdotta è trascurabile
05FTM.43
QPsw
Esempio numerico
Dati i seguenti N=10 valori 7 7 10 15 23 27 29 35 47 99
calcolare il primo quartile, la mediana ed il terzo quartile.
• L’indice del primo quartile Q1 vale:
I25 = (10+1)×25 /100 = 2.75 --> Q1 cade tra il secondo ed il terzo valore
Quindi Q1= x2 + (x3 – x2) × 0.75 = 7+(10-7) × 0.75 =9.25
• La mediana Me (o Q2) è pari a (23+27)/2=25
• L’indice del terzo quartile Q3 vale:
I75 = (10+1)×75 /100 = 8.25 -> Q3 cade tra l'ottavo ed il nono valore
Quindi Q1= x8 + (x9 – x8) × 0.25 = 35+(47-35) × 0.25 =38
QPsw
05FTM.44
Quartili e percentili con Excel
QPsw
05FTM.45
Rappresentazione grafica delle grandezze
calcolate: Boxplot
QPsw
05FTM.46
Boxplot con Excel
(occorre una macro)
05FTM.47
QPsw
Distribuzione con Excel
QPsw
05FTM.48
Un esempio interessante
• ....
05FTM.49
QPsw
Qualità di una misura: Affidabilità
•
Le misure, a loro volta, posseggono delle qualità che, in alcuni casi, è
possibile quantificare in modo formale.
•
Affidabilità (reliability). L'affidabilità è relativa ai valori che si ottengono
effettuando più volte la stessa misura. Se i valori ottenuti sono vicini tra loro la
metrica è affidabile.
–
–
QPsw
Tipicamente si caratterizza questa qualità analizzando la varianza σ2 di misure
ripetute.
Più piccolo è questo valore più la metrica è affidabile. Una possibile alternativa
è l'indice di variazione che "normalizza" rispetto alla media: σ/media.
05FTM.50
Qualità di una misura(2)
• Validità (validity). La validità indica se la metrica misura
effettivamente cosa vogliamo misurare. Per misure poco astratte
(peso, volume) la validità coincide con l'accuratezza. Si noti che anche
per misure poco astratte i concetti di affidabilità e validità sono
differenti: un orologio fermo è perfettamente affidabile ma ha una
validità molto ridotta...
• Per concetti astratti la validità di una misura può essere molto
complessa a valutarsi (e.g., la religiosità di una comunità misurata
tramite le presenze in chiesa).
05FTM.51
QPsw
Affidabilità e validità di una misura
Affidabile ma
non valida
QPsw
Valida ma
non
affidabile
Affidabile
e Valida
05FTM.52
Errori di misura (1)
• l risultato di un’operazione di misura è un numero reale M che dovrebbe
catturare il valore vero T del fenomeno in esame
• L’esperienza indica che, se si eseguono più misurazioni di una stessa
quantità, raramente le misure coincidono
– I valori misurati (M) sono in genere diversi dal vero valore T
• La differenza tra il valore misurato e quello vero è detta errore totale (ET)
M = T + ET
misura
valore
vero
errore
totale
05FTM.53
QPsw
Errori di misura (2)
• La misurazione non consente di determinare con certezza il vero
valore della quantità misurata, ma produce stime la cui capacità di
approssimare il vero valore (attendibilità) dipende dal metodo
analitico e da come è stato eseguito il procedimento analitico.
– È necessario considerare la natura degli errori di misura
ET = Egrossolani + Esistematici + Ecasuali
Si prevengono con un’accorta
organizzazione dell’analisi
QPsw
Costituiscono oggetto tipico della
metodologia statistica
Esistematici
Influenzano la validità
Ecasuali
Influenzano l’affidabilità
05FTM.54
Errori di misura (3)
• Gli errori sistematici influenzano la validità e, come dice il nome, si
verificano in modo costante. Si pensi, per esempio, ad una bilancia per
pesare le persone tarata male che aggiunge sistematicamente 1 kg al
peso reale:
– misura= T + 1kg + variazione casuale ovvero M= T + Es + Ec
• la misura non è valida
– se assumiamo che il termine Es non sia presente, ovvero che ci siano
solo errori casuali la formula vale:
– M= T + Ec
– se il termine Ec è relativo ad un fenomeno veramente casuale il suo
contributo medio è nullo (valore atteso E(Ec)=0) e, quindi, la media di
infinite misure E(M)=T e quindi la misura è valida.
• una tipica tecnica che sfrutta questo principio è quella di ripetere la misura
N volte e farne la media
05FTM.55
QPsw
Errori di misura(4)
• Qual'è l'effetto di un errore casuale e sull' affidabilità? Intuitivamente
più e è piccolo meno influisce. In formule:
M = T + Ec
e quindi
var(M)= var(T) + var(Ec)
• si definisce formalmente l'affidabilità di una misura come il rapporto tra
la varianza della quantità misurata e la varianza della misura:
ρm=var(T)/var(M) = [var(M)-var(Ec)]/var(M)= 1- [var(Ec)/var(M)]
• Utilizzando questa definizione, l'affidabilità oscilla tra 1 e 0
• Riassumendo
– Gli errori sistematici influenzano la validità
– Gli errori casuali influenzano l'affidabilità
QPsw
05FTM.56
Valutare l'affidabilità
• Ci sono vari modi per valutare l'affidabilità definita come var(T)/var(M)
• Uno dei metodi più adatti al contesto del sw è quello del doppio test
• L'idea è quella di effettuare più volte una doppia misura
M1 = T + Ec1
M2 = T + Ec2
• e poi di effettuare la correlazione tra le varie misure ottenendo proprio
l'affidabilità
• ρm = Correlazione(M1,M2)=var(T)/var(M)
• Ovviamente le attività di misura automatiche hanno affidabilità pari ad 1
ed il metodo del doppio test ha senso su attività manuali tipo ispezioni.
• Ad esempio è possibile fare eseguire la stesse attività di ispezione a due
persone, e.g., contare le deviazioni dallo standard della stessa classe
Java. Se questa attività viene ripetuta più volte è possibile calcolare
l'affidabilità del processo ispettivo.
05FTM.57
QPsw
Correlazione
• Indica l'esistenza o meno di una relazione tra due variabili
• La più nota è la correlazione di Pearson che varia da -1 (correlazione
negativa) a +1 (correlazione postiva)
• Valida solo per relazioni lineari
QPsw
05FTM.58
Esempi
M2
M2
M2
M1
+1
M1
-1
M1
0
05FTM.59
QPsw
Correlazione con Excel
QPsw
05FTM.60
Statistica inferenziale
05FTM.61
QPsw
Grandezze di interesse
• Si vuole analizzare una popolazione di M elementi (M non è noto)
tramite un campione di N elementi {x1,...,xn}, e si definiscono i
seguenti parametri:
• media (campionaria) m = (x1+ x2+... +xN)/N
• varianza (campionaria) var=[(x1-m)2+ (x2-m)2 +...(xN-m)2]/(N-1)
• deviazione standard (campionaria) σ=var1/2
• percentili / mediana / moda /
• i parametri in questione sono variabili casuali, il cui valore dipende
dalla casualità del campionamento
• tipicamente (auspicabilmente) gli elementi del campione si
distribuiscono secondo una distribuzione normale (o gaussiana) e
questo permette di effettuare delle stime
– o, se così non è, si assume che lo sia....
– analisi Montecarlo...
QPsw
05FTM.62
Qual'è il problema?
• Stiamo lavorando con qualla che viene chiamata statistica inferenziale
(vs descrittiva) ovvero stiamo cercando di inferire delle proprietà
usando un campione dei dati.
• La caratterizzazione statistica del nostro campione (in particolare la
media) differisce da quella dei dati reali
• All'aumentare della dimensione del campione la differenza tende a
diminuire
• Ma come varia questa differenza?
• La statistica inferenziale permette di stimare (probabilisticamente)
l'errore commesso
05FTM.63
QPsw
Intervallo di confidenza
• Sotto l'assunzione di distribuzione normale è possibile stimare la
probabilità che la media di un campione di dimensione N si discosti più
di una certa quantità dalla media "vera"
• Lo scarto è legato alla probabilità di errore che siamo disposti a
sopportare ed è direttamente proporzionale alla deviazione standard
del campione ed inversamente proporzionale al numero di campioni
N1/2
• Un parametro di riferimento tipico è il 95% e le formule ci dicono che
nel 95% dei casi un campione mostrerà uno scostamento dalla media
"vera" inferiore a:
–
–
–
–
2.77*σ/N1/2 per N=5
2.26*σ/N1/2 per N=10
2.09*σ/N1/2 per N=40
1.96*σ/N1/2 per N "grande" (Unica implementata da Excel)
• N.B. Per dimezzare l'intervallo di confidenza occorre quadriplicare il
numero dei campioni
QPsw
05FTM.64
Intervallo di confidenza
95%
dei dati
m-1.96 σ
m
m+1.96 σ
1.96*σ/N1/2 per N "grande"
Possiamo diminuire od aumentare la probabilità di errore
(usando formule con parametri diversi)
L'intervallo di confidenza varia in modo inverso:
probabilità di errore più bassa: intervallo di confidenza più grande
05FTM.65
QPsw
Esempio
• Raccolgo 10 voti 26, 21, 29, 26, 21, 28, 27, 26, 29, 27
• m= 26
• σ= 2.87
• 2.26*σ/101/2 =2.05
• quindi la media vera (26.29), al 95%, cade nell'intervallo
[26-2.05, 26+2.05] = [23.95, 28.05]
•
•
•
•
•
QPsw
Se prendo 20 voti
m= 26.75
σ= 3.02
2.26*σ/201/2 =1.41
quindi la media vera (26.29), al 95%, cade nell'intervallo
[26.75-1.41, 26.75+1.41] = [25.34, 28.16]
05FTM.66
Verifica d'ipotesi
05FTM.67
QPsw
Verifica d’ipotesi(1)
• Molto spesso nell’ambito della ricerca sperimentale è necessario
confrontare tra loro serie di misure ripetute (es. confronto di risultati di
due o più metodi)
– Il confronto può essere condotto mediante appropriati test statistici
– I test statistici consistono nel mettere alla prova l’ipotesi che certi
parametri delle popolazioni (es. medie ) siano uguali
– l'ipotesi che le medie "vere" siano tutte uguali (e quindi che le
differenze osservate siano casuali) è detta ipotesi nulla
– Il test viene condotto fissando a priori la probabilità di errore che
potenzialmente può essere commesso (α)
QPsw
05FTM.68
Verifica d’ipotesi(2)
• Un’ipotesi statistica è una asserzione o supposizione sulla distribuzione di
una o più variabili casuali e si indica con la lettera H
• Il test può essere ricondotto alla seguente domanda:
– presi due campioni della stessa misura , Ca e Cb, con che probabilità posso
affermare che appartengono alla stessa popolazione ?
• Generalmente si mettono a confronto due ipotesi, contrarie tra loro:
– Ipotesi H0 (IPOTESI NULLA). Costituisce l’oggetto della verifica: specifica i
valori dei parametri della popolazione da cui si suppone provenga il campione
in esame
H 0 : Θa = Θ b
• Dove Θ indica il parametro di interesse (generalmente la media)
– Ipotesi H1 (IPOTESI ALTERNATIVA). Contraria alla precedente
H1: Θa != Θb
• Il tutto sempre condizionato ad una certa probabilità di errore (α)
• Il tipico valore di soglia è α=0.05:
– α > 0.05 -> scegliamo H0
– α <=0.05 -> scegliamo H1
05FTM.69
QPsw
Esempio (1)
• Supponiamo di aver sviluppato due interfacce per la stessa
applicazione e vogliamo capire quale delle due riscuota la maggiore
soddisfazione da parte degli utenti
• Intervistiamo 7 utenti che hanno utilizzato il prototipo Pa e 7 utenti che
hanno usato il prototipo Pb
• Analizziamo in quest’esempio le risposte alla domanda che indaga la
soddisfazione del cliente
– le risposte ammissibili sono valori da 1 a 6 dove 1 indica un basso
grado di soddisfazione e sei un alto grado di soddisfazione (N.B. NON
è una scala di Likert, ma è un voto: è almeno una scala a intervalli)
• Nella tabella che segue sono riportate le risposte ottenute con le due
indagini
μ a . = (1 + 6 + 1 + 1 + 6 + 6 + 2 ) / 7 = 3, 286
μ b . = (5 + 3 + 1 + 6 + 2 + 4 + 1) / 7 = 3,143
QPsw
05FTM.70
Esempio(2)
• La differenza osservata è reale ?
{
H0: (ipotesi nulla): μa=μb
H1: (altra ipotesi): μa≠μb
SE È VERA H0
SE È VERA H1
... e in base al
campione
decido che
è vera H0
decisione
giusta
protezione:
(1-α)
decisione
sbagliata
errore di tipo II:
β
... e in base al
campione
decido che
è vera H1
decisione
sbagliata
errore di tipo I:
α
decisione
giusta
potenza:
(1-β)
Protezione (1-α):
probabilità di accettare H0 quando è vera H0
Potenza del test (1-β):
probabilità di rifiutare H0 quando è vera una specifica H1
Rischio di errore di tipo I (α):
probabilità di rifiutare H0 quando è vera H0
Rischio di errore di tipo II (β):
probabilità di accettare H0 quando è vera una specifica H1
05FTM.71
QPsw
Confronto tra due campioni
• Se i campioni da confrontare sono due possiamo utilizzare l'intervallo
di confidenza
cm2
due medie
QPsw
cm1
cm1
cm1
cm2
due intervalli di confidenza
che potenzialmente sottointendono
una media comune
cm2
due intervalli di confidenza
che potenzialmente
NON sottointendono
una media comune
05FTM.72
t-test
• La tecnica è nota con il nome di t-test, confrontando la differenza delle
medie con la dispersione dei dati (espressa tramite la deviazione
standard)
| μa − μb |
t=
σa +σb
2
2
= 0 ,126
n
• Il valore trovato si confronta con la distribuzione di t, tipicamente
espressa tramite una tabella che indica la probabilità α che la
differenza delle medie sia casuale
05FTM.73
QPsw
Tabella t-test
α
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
0.10
3.078
1.886
1.638
1.533
1.476
1.440
1.415
1.397
1.383
1.372
1.363
1.356
1.350
1.345
1.341
1.337
0.05
6.314
2.920
2.353
2.132
2.015
1.943
1.895
1.860
1.833
1.812
1.796
1.782
1.771
1.761
1.753
1.746
0.025
12.706
4.303
3.182
2.776
2.571
2.447
2.365
2.306
2.262
2.228
2.201
2.179
2.160
2.145
2.131
2.120
0.01
31.821
6.965
4.541
3.747
3.365
3.143
2.998
2.896
2.821
2.764
2.718
2.681
2.650
2.624
2.602
2.583
0.005
0.001
63.657 318.313
9.925 22.327
5.841 10.215
4.604
7.173
4.032
5.893
3.707
5.208
3.499
4.782
3.355
4.499
3.250
4.296
3.169
4.143
3.106
4.024
3.055
3.929
3.012
3.852
2.977
3.787
2.947
3.733
2.921
3.686
...
Distribuzione di t per 10 gradi
di libertà
Si distinguono i casi a due code (α/2)
da i casi ad una coda (α)
QPsw
t
05FTM.74
Tabella t-test
0.10
μ a . = (1 + 6 + 1 + 1 + 6 + 6 + 2 ) / 7 = 3, 286
μ b . = (5 + 3 + 1 + 5 + 2 + 4 + 2 ) / 7 = 3,143
t=
| μa − μb |
σ a2 + σ b2
n
= 0 ,126
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
3.078
1.886
1.638
1.533
1.476
1.440
1.415
1.397
1.383
1.372
1.363
1.356
1.350
1.345
1.341
1.337
0.05
6.314
2.920
2.353
2.132
2.015
1.943
1.895
1.860
1.833
1.812
1.796
1.782
1.771
1.761
1.753
1.746
0.025
12.706
4.303
3.182
2.776
2.571
2.447
2.365
2.306
2.262
2.228
2.201
2.179
2.160
2.145
2.131
2.120
0.01
31.821
6.965
4.541
3.747
3.365
3.143
2.998
2.896
2.821
2.764
2.718
2.681
2.650
2.624
2.602
2.583
0.005
0.001
63.657 318.313
9.925 22.327
5.841 10.215
4.604
7.173
4.032
5.893
3.707
5.208
3.499
4.782
3.355
4.499
3.250
4.296
3.169
4.143
3.106
4.024
3.055
3.929
3.012
3.852
2.977
3.787
2.947
3.733
2.921
3.686
• Si calcolano i gradi di libertà: 7+7-2=12 e si cerca nella riga
corrispondente il valore corrispondente alla probabilità a che ci
interessa (α/2 nel caso di due code), ovvero 0.025-->2.179
• Il t trovato, 0.126 NON è maggior di 2.179 quindi α è più grande di
0.05 e dobbiamo scegliere l'ipotesi nulla
05FTM.75
QPsw
T-test con Excel
QPsw
05FTM.76
Altro esempio
μ a . = (3 + 4 + 4 + 4 + 4 + 4 + 3) / 7 = 3,714
μ b . = (3 + 3 + 3 + 3 + 3 + 4 + 3) / 7 = 3,143
t=
| μa − μb |
σa +σb
2
2
= 2 , 449
n
05FTM.77
QPsw
Tabella t-test
0.10
0.05
0.025
0.01
0.005
0.001
μ a . = ( 3 + 4 + 4 + 4 + 4 + 4 + 3) / 7 = 3,714
μ b . = (3 + 3 + 3 + 3 + 3 + 4 + 3) / 7 = 3,143
t=
| μa − μb |
σ a2 + σ b2
n
= 2 , 449
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
3.078
1.886
1.638
1.533
1.476
1.440
1.415
1.397
1.383
1.372
1.363
1.356
1.350
1.345
1.341
1.337
6.314
2.920
2.353
2.132
2.015
1.943
1.895
1.860
1.833
1.812
1.796
1.782
1.771
1.761
1.753
1.746
12.706
4.303
3.182
2.776
2.571
2.447
2.365
2.306
2.262
2.228
2.201
2.179
2.160
2.145
2.131
2.120
31.821
6.965
4.541
3.747
3.365
3.143
2.998
2.896
2.821
2.764
2.718
2.681
2.650
2.624
2.602
2.583
63.657 318.313
9.925 22.327
5.841 10.215
4.604
7.173
4.032
5.893
3.707
5.208
3.499
4.782
3.355
4.499
3.250
4.296
3.169
4.143
3.106
4.024
3.055
3.929
3.012
3.852
2.977
3.787
2.947
3.733
2.921
3.686
• Si calcolano i gradi di libertà: 7+7-2=12 e si cerca nella riga
corrispondente il valore corrispondente alla probabilità a che ci
interessa (α/2 nel caso di due code), ovvero 0.025-->2.179
• Il t trovato, 2.449 é maggior di 2.179 quindi α è più piccolo di 0.05 e
possiamo scartare l'ipotesi nulla
QPsw
05FTM.78
T-test con Excel
05FTM.79
QPsw
Valori comuni di α (p-value)
• Un α pari a 0.05 ci dice che c'è la possibilità del 5% che la differenza
di media trovata
• 0.05 è considerato un valore di confine ed in letteratura si comincia a
prendere in considerazione la validità di una analisi per p<=0.01. Se
p<=0.005 l'analisi è classificata statisticamente significativa e per
p<=0.001 altamente significativa
• Ovviamente sono solo valori arbitrari, anche se largamente utilizzati
QPsw
05FTM.80
Quindi
• Se decido di scegliere H1 ho una probabilità di errore pari ad α
• Se decido di scegliere H0 ho una probabilità di errore pari a (1-α)
05FTM.81
QPsw
E se ho più di 2 campioni ?
• se si effettuano tre n*(n-1)/2 t-test con α=0.05 la probabilità di trovare
tre differenze è 0.95x0.95x0.95= 0.86
• con n=5 sono necessari 10 confronti....
• In generale per n>2 campioni su utilizza una tecnica di analisi della
varianza (ANOVA) concettualmente simile al ttest ma che prende in
considerazione tutte le medie insieme
QPsw
05FTM.82
ANalysisOfVAriance
•
L’analisi della varianza (ANOVA) è un test statistico per la verifica d’ipotesi
•
L’ANOVA è un insieme di tecniche statistiche facenti parte della statistica inferenziale che
permettono di confrontare due o più gruppi di dati confrontando la variabilità interna a questi
gruppi con la variabilità tra gruppi
•
L’ipotesi nulla solitamente prevede che i dati di tutti i gruppi abbiano la stessa origine, ovvero
la stessa distribuzione stocastica, e che le differenze osservate tra i gruppi siano dovute
solo al caso
•
Il confronto si basa sull’idea che se la variabilità interna ai gruppi è relativamente elevata
rispetto alla variabilità tra i gruppi, allora probabilmente la differenza tra questi gruppi è
soltanto il risultato della variabilità interna.
•
Il più noto insieme di tecniche si basa sul confronto della varianza e usa variabili di test
distribuite come la variabile casuale F di Snedecor
•
Nota Bene: t-test ed Anova su due gruppi sono perfettamente equivalenti
QPsw
Analisi statistica dei dati
05FTM.83
Come funziona
•
Qual è la logica dell’ANOVA?
•
quali ipotesi sono sottoposte a verifica e quale ragionamento porta all’accettazione
o al rifiuto di esse?
¾ Nell’ANOVA le ipotesi sono:
H0: μ1 = μ2 =…μK
H1: almeno 2 delle medie sono differenti
QPsw
Analisi statistica dei dati
05FTM.84
Come funziona
•
Per confrontare i risultati dei diversi esperimenti (es. per controllare l’effetto dei
diversi livelli di controllo del sw, ossia per testare la differenza tra le medie dei
gruppi sottoposti ai diversi livelli di controllo), separiamo la variabilità
complessiva della variabile dipendente in due fonti di variabilità:
•
Varianza Between (VarB): attribuibile alla varianza tra gruppi
•
Varianza Within (VarW): residua all’interno dei gruppi, varianza entro i
gruppi
¾ Dal confronto delle due varianze possiamo decidere se le differenze osservate
nei diversi esperimenti sono significative, ossia se rappresentano
effettivamente due popolazioni differenti (es. i controlli diversi hanno avuto
effetto oppure no) oppure sono una manifestazione casuale
¾ NB: lavoriamo sulla scomposizione della varianza, ma stiamo facendo
inferenza sulle medie
05FTM.85
QPsw
Come funziona
•
L’ANOVA, si applica nel caso si vogliano confrontare gli effetti medi di una
variabile su I campioni distinti: {C1,…,CI }.
•
Ciascun campione è assunto avere lo stesso numero J di soggetti (ma non è
obbligatorio)
Yij
è la j-esima osservazione sull’ i-esimo campione
Dove:
J
−
Media del campione i :
μ i = ( ∑ Yij ) / J
j =1
I
−
media generale:
μ = (∑ μ i ) / I
i =1
QPsw
05FTM.86
Come funziona
IDENTITA’ PRINCIPALE DELL’ANOVA (somma dei quadrati)
SS totale = SSW + SSB
Ovvero:
I
J
∑ ∑ (Y
i =1
Dove:
− μ ) =∑
ij
j =1
I
2
i =1
J
∑ (Y
j =1
ij
− μi ) + J ∑ (μi − μ )2
i =1
J
I
μ i = ( ∑ Yij ) / J
SS B = J ∑ ( μ i − μ ) 2
j =1
I
J
i =1
j
i =1
μ = ( ∑ ∑ Yij ) / IJ
I
SS W = ∑
i =1
I
2
I
SS T = ∑
i =1
J
∑ (Y
j =1
ij
J
∑ (Y
j =1
ij
− μ )2
− μi )2
05FTM.87
QPsw
Test di Fisher
•
Dalla teoria dei valori attesi si ricava:
F =
•
SS B /( I − 1)
SS W /[ I ( J − 1)]
FI −1, ( I ( J −1))
È stato dimostrato che questo test ha una distribuzione campionaria F di
Snedecor con (I-1) e (I(J-1)) gradi di libertà
(F(I-1),(I(J-1)) )
•
noti tali gradi di libertà (numeratore e denominatore) è possibile valutare la
probabilità associata ai valori di F
•
per un valore α (p-value) prefissato, solitamente α=0.05, questo test ci dice
quando l’ipotesi nulla è accettata (
F(I-1),(I(J-1)) )
QPsw
~
F<F(I-1),(I(J-1)) ) e quando viene rifiutata ( F>
05FTM.88
Test di Fisher
• Criterio decisionale:
⎧⎪ accetto se F <= FI −1, I ( J −1)
H0 = ⎨
⎪⎩ rifiuto se F > FI −1, I ( J −1)
05FTM.89
QPsw
Esempio
QPsw
05FTM.90
Esempio (2 campioni per semplicità)
μ a = (1 + 6 + 1 + 1 + 6 + 6 + 2 ) / 7 = 3, 28
μ b = (5 + 3 + 1 + 6 + 2 + 4 + 1) / 7 = 3,14
μ = (1 + 6 + 1 + 1 + 6 + 6 + 2 + 5 + 3 + 1 + 5 + 2 + 4 + 2 ) / 14 = 3, 21
SS B = 7[( 3, 28 − 3, 21) 2 + (3,14 − 3, 21) 2 ] = 0,0714
SS W = (1 − 3, 28 ) 2 + ( 6 − 3, 28 ) 2 + (1 − 3, 28 ) 2 + (1 − 3, 28 ) 2 + ( 6 − 3, 28 ) 2 + ( 6 − 3, 28 ) 2 + ( 2 − 3, 28 ) 2 +
+ (5 − 3,14 ) 2 + (3 − 3,14 ) 2 + (1 − 3,14 ) 2 + ( 6 − 3,14 ) 2 + ( 2 − 3,14 ) 2 + ( 4 − 3,14 ) 2 + (1 − 3,14 ) 2 = 62 , 29
F =
0,0714 /( 2 − 1)
= 0,01376
62 , 29 /[ 2 ( 7 − 1)]
F1,12 = 4 ,75
<<
Accetto Ho
05FTM.91
QPsw
Esempio con Excel
Analisi varianza: ad un fattore
RIEPILOGO
Gruppi
Colonna 1
Colonna 2
Conteggio
7
7
Somma
Media
Varianza
23 3,285714 6,571429
22 3,142857 3,809524
ANALISI VARIANZA
Origine della variazione
Tra gruppi
In gruppi
SQ
0,071429
62,28571
Totale
62,35714
QPsw
gdl
MQ
F
Valore di significatività
F crit
1 0,071429 0,013761
0,908555546 4,747225
12 5,190476
13
05FTM.92
Analisi della varianza ANOVA sulla relazione
linee testate e andamento dei difetti
• Quasi sempre il tentativo di dimostrare una ipotesi si concretizza nel
cercare una relazione tra due variabili: se modifico A allora B cambia
(in un certo modo)
• Ad esempio: cerco di dimostrare che se aumento la proporzione KT di
linee di codice testate l'andamento dei difetti DR nel primo anno dopo
il rilascio diminuisce
• proporzione KT=KLOC testate/KLOC (per comodità la esprimo come
percentuale)
• andamento DR=(D/KLOC)*k (poniamo k=1)
05FTM.93
QPsw
Variabili dipendenti ed indipendenti
• In queste analisi si indicano col nome indipendenti le variabili che
vengono manipolate per verificare una ipotesi e col nome dipendenti le
variabili che vengono solo osservate e che dipendono (si spera) da
quelle manipolate.
• Nel nostro esempio
• KT=variabile indipendente
• DR=variabile dipendente
QPsw
05FTM.94
Il nostro insieme campione
• Assumiamo, per semplicità espositiva, che nella sw house osservata si
conducano attività di test per tre differenti percentuali prefissate:
• 50 %
70%
90%
• e che, per ciascuna di esse, siano stati osservati per un anno 5
pacchetti software.
• Calcoliamo la media di DR ed otteniamo la seguente tabella
Anova ci permette di valutare la
probabilità che le medie siano
differenti per caso
QPsw
05FTM.95
Altamente
Significativo
QPsw
05FTM.96
Per nulla
Significativo
05FTM.97
QPsw
Post hoc test (1)
• L'esperimento appena effettuato ci dice che i tre
campioni non appartengono alla stessa popolazione
(ovvero che la probabilità che i tre campioni
appartengano alla stessa popolazione è
α=0.000166)
• Questo non implica che appartengono a tre
popolazioni differenti! Ad esempio il gruppo al 70%
ed il grupppo al 90% potrebbero avere la stessa
media...
• E' quindi necessario confrontare le singole coppie
n*(n-1)/2=3
• Il problema è stato analizzato negli ultimi 50 anni ed
ancora manca una soluzione definitiva
QPsw
05FTM.98
Post hoc test : Fisher protected test
•
•
E' il metodo più applicato e prevede di
utilizzare i test a coppie solo dopo che
anova ha confermato la significatività
delle differenze
Ad esempio
1. 50, 70 e 90 non hanno la stessa
media (p=0.000166) Anova a 3
2. 50 e 70 hanno medie differenti
(P1=0.012) Anova a 2 o t-test
3. 70 e 90 hanno medie differenti
(P2=0.010) Anova a 2 o t-test
4. 50 e 90 hanno medie differenti
(P3=0.00037) Anova a 2 o t-test
•
In questo caso possiamo anche
affermare che 50, 70 e 90 hanno le
medie tutte differenti :
– (1-p1)(1-p2)(1-p3)=0.977 e
– P123=1-0.977=0.022
50-70
70-90
50-90
05FTM.99
QPsw
Esercitazione conclusiva su ANOVA
QPsw
05FTM.100
Esperimento sul naming convenction
• Il sistema qualità della sw house Acme sta studiando l'influenza della naming
convenction sulla leggibilità del codice con particolare attenzione alla fase di
integrazione.
• In particolare, il sistema qualità ha messo a punto 3 differenti tecniche di naming
convenction NC1, NC2, NC3 e vuole indagare se esista una relazione tra la
tecnica adottata ed il numero di errori individuati in fase di test di integrazione
• Progetto di un esperimento per validare questa ipotesi.
05FTM.101
QPsw
Variabili dipendenti ed indipendenti
Struttura dell'esperimento
• Variabile indipendente: tipo di naming convenction adottata
• Variabile dipendente: numero di errori trovati durante il test di
integrazione per KLOC
• Le differenti tecniche di naming convenction vengono impegate in tre
progetti simili (si cerca di eliminare l'influenza di altri fattori), A, B, C.
• I programmatori coinvolti nei progetti e la metodologia di gestione dei
progetti sono simili.
• Durante la fase di integrazione si analizzano 6 classi del progetto A,
sei del progetto B e sei del progetto C, ottenendo i seguenti valori:
– A (15, 14, 20, 22, 19, 20) media 18.3 var 9.9
– B (23, 25, 22, 28, 19, 20) media 22.8 var 11.0
– C (15, 16, 15, 18, 16, 22) media 17.0 var 7.2
QPsw
05FTM.102
3 Ipotesi per applicare ANOVA
• 1 ) Indipendenza
– k campioni presi in modo casuale da k popolazioni
• 2) Distribuzione normale
– i k campioni presentano una distribuzione normale
– oppure la distribuzione di piccoli campioni è grossomodo simmetrica
(boxplot)
– oppure campione grande (n>30) : teorema del limite centrale
– In alternativa: test non parametrici...
• 3) Stessa varianza
– i k campioni presentano la stessa varianza
– Test di Levene (non in Excel!)
– oppure test empirco (Excel) rapp massimo 2
05FTM.103
QPsw
Distribuzione normale ?
Ragionevolmente simmetriche rispetto alla media
QPsw
05FTM.104
Altrimenti : Teorema del limite centrale
• Si consideri una successione di variabili casuali
indipendenti e
identicamente distribuite, e in particolare tali che esistano, finiti, i loro
momenti di ordine primo e secondo, e sia
• definita allora la nuova variabile casuale:
dove x è la media aritmetica degli xj, si ha che Sn converge a una
variabile casuale normale avente valore atteso 0 e varianza 1
05FTM.105
QPsw
Assumiamo le ipotesi soddisfatte:
Anova single factor
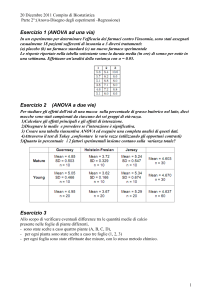
Ipotesi nulla Ho-> mediaA=mediaB=mediaC
Possiamo rifiutare l'ipotesi nulla (P=0.00834)
Qundi ALMENO una media è differente
QPsw
05FTM.106
Post hoc test : Fisher protected test
• A valle di un test ANOVA che ha rifiutato l'ipotesi nulla possiamo
effettuare n(n-1) ttest
B>A
B>C
media A = media B
Quindi sicuramente possiamo scartare B
Non siamo in grado di scegliere tra A e C
QPsw
05FTM.107