ANOVA (Analysis of Variance)
Paola Lecca – CIBIO unitn
Corso di Matematica e Statistica 2
Queste slides sono state preparate riferendosi al testo
S. M. Iacus a G: Masarotto
Laboratorio di Statistica con R, McGraw-Hill
Regressione multilineare
Molto spesso è riduttivo pensare a modelli matematici di fenomeni naturali in cui solo le
variabili X e Y sono coinvolte.
Se Y è la variabile indipendente ( o variabile ”risposta”), in molte situazionii l’andamento
di Y può essere governato da più di una variabile.
sono detti regressori, mentre
coefficienti di regressione.
sono detti
Applicazione in R
Modello a due regressori x1 e x2. Esempio in R.
x1 <- runif(50)
x2 <- sin(runif(50))
y <- 4 + 2*x1 - x2 +rnorm(50)
lm(y ~ x1 + x2)
Call:
lm(formula = y ~ x1 + x2)
Coefficients:
(Intercept)
x1
3.817
2.169
x2
-0.923
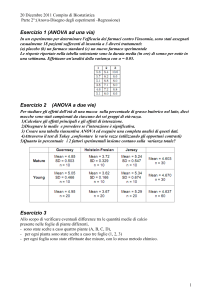
Analisi della varianza (ad una via)
Un’applicazione notevole della regressione multidimensionale è l’analisi della varianza.
Il problema è il seguente:
si supponga di avere k gruppi di individue cui viene sperimentato un particolare
trattamento diverso per ogni gruppo;
indichiamo con
l’individuo numero j del gruppo i
indichiamo con
la media del gruppo i e con
Si può allora scrivere
nel modo seguente
la media complessiva.
Calcolo della devianza
La devianza delle
SST
(Total sum of squares)
è
SSB
(Sum of squares between groups)
SST = SSB + SSW
SSW
(Sum of squares within groups)
Calcolo della varianza
Se calcoliamo le varianze
sotto l’ipotesi di normalità si ha
Ci si aspetta che il rapporto
Statistica F
Sia maggiore di 1 se la differenza tra la media dei gruppi spiega la maggior parte di
variabilità del modello
Test di ipotesi
Si può quindi effettuare un test di ipotesi
H0: tutti gli
H1: almeno un
sono ugali
è diverso dagli altri.
In R un test di questo tipo si può effettuare utilizzando il comando lm e il comando
anova.
In pratica stiamo affrontando il problema di un test di ipotsi attraverso il ricorso
alla’nalisi della varianza.
Il comando anova in R: esempio
Tipo di
strutto
1
2
3
4
64
78
75
55
72
91
93
66
68
97
78
49
77
82
71
64
56
85
63
70
95
77
76
68
Esempio: i bomboloni di Lowe: grammi di materia grassa assorbita dai bomboloni
in realzione al tipo di strutto utilizzato per la cottura.
Si vuole verificare se l’assorbimento di materia grassa nella cottura varia al variare
del prodotto utilizzato per la frittura.
Soluzione in R
> x <- c(rep(1, 6), rep(2, 6), rep(3, 6), rep(4, 6))
> y <- c(64, 72, 68, 77, 56, 95,
+
78, 91, 97, 83, 85, 77,
+
75, 93, 78, 71, 63, 76,
+
55, 66, 49, 64, 79, 68)
>
> bomboloni <- data.frame(y, x)
>
> x <- factor(x)
>
> model <- lm(y ~ x)
> model
Questi numeri indicano le deviazioni
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept)
x2
72.00
13.17
x3
4.00
x4
-8.50
> anova(model)
Analysis of Variance Table
Response: y
Df Sum Sq Mean Sq F value Pr(>F)
x
3 1457.0 485.67 4.3669 0.01609 *
Residuals 20 2224.3 111.22
--Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Il comando anova genera
una tabella.
Abbiamo trovato che il test è
significativo e quindi si rifiuta
l’ipotesi nulla.
La tabella ANOVA
Fonte di
variabilità
Gradi di
libertà
SS
MS
Statistica F
p-value
Regressio
ne
1
SSB
MSB
F= MSB/MSW
Pr(> F)
Residui
n-2
SSW
MSW
Totale
n-1
SST