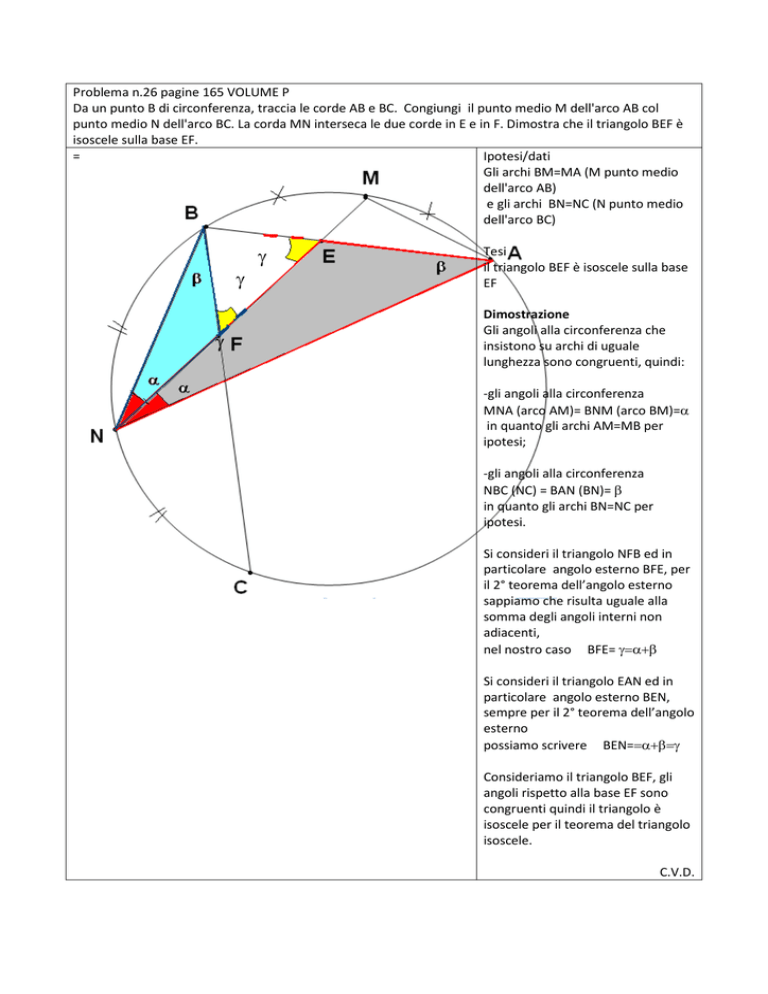
Problema n.26 pagine 165 VOLUME P
Da un punto B di circonferenza, traccia le corde AB e BC. Congiungi il punto medio M dell'arco AB col
punto medio N dell'arco BC. La corda MN interseca le due corde in E e in F. Dimostra che il triangolo BEF è
isoscele sulla base EF.
=
Ipotesi/dati
Gli archi BM=MA (M punto medio
dell'arco AB)
e gli archi BN=NC (N punto medio
dell'arco BC)
γ
γ
γ
Tesi
il triangolo BEF è isoscele sulla base
EF
Dimostrazione
Gli angoli alla circonferenza che
insistono su archi di uguale
lunghezza sono congruenti, quindi:
-gli angoli alla circonferenza
MNA (arco AM)= BNM (arco BM)=α
in quanto gli archi AM=MB per
ipotesi;
-gli angoli alla circonferenza
NBC (NC) = BAN (BN)= β
in quanto gli archi BN=NC per
ipotesi.
Si consideri il triangolo NFB ed in
particolare angolo esterno BFE, per
il 2° teorema dell’angolo esterno
sappiamo che risulta uguale alla
somma degli angoli interni non
adiacenti,
nel nostro caso BFE= γ=α+β
Si consideri il triangolo EAN ed in
particolare angolo esterno BEN,
sempre per il 2° teorema dell’angolo
esterno
possiamo scrivere BEN==α+β=γ
Consideriamo il triangolo BEF, gli
angoli rispetto alla base EF sono
congruenti quindi il triangolo è
isoscele per il teorema del triangolo
isoscele.
C.V.D.












