!
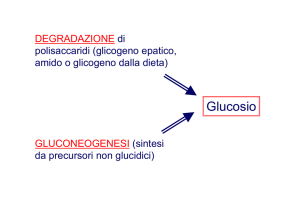
"
#
$
2"
&
!
%
%&
& %&
&
&
%&
"
%
%&
&%
&
&
%&
&
%&
&
%&
&
%
&
%&
&
%&
&
%&
& % %'
& %&
( )
0
&
&
&
&
&%
"
+ ()
"
"
+ (&
*
!
%
%
&'
%
,
. "
- "
+ ()
/
,
+ (&
. "
"
- "
#
( )
#
1
/
&)
+ (&
%&
%
&'
%
" - "
+
()
%
,
- "
%
&)
*
+ ()
"
1
2
32
"
3
0
"
" "
3
"
"
0
"
"
"
0
"
$
"
"
0
4
" "
. 0
4
4 5/
#
'
2
3 2
"
0
3 2"
7
0
"
"
"
"0
"
" 8
"
9
#& %# ) #% → # % ) #& %
3 :; "
"
-- "
"0
. * /
#
6
2
2
3 ="
"
0
0
" " - "
0 0
9
$
$
0
0
.
.
0 0
4
" /
0
/
#
<
!
3 *0
- "
"
"
- "
"
"
" " "
3 >0 "
- "
3 :
?
;
"
"
;
@0
"
" 0"
A
#
#
3
C
- "
3 :
?
0"
$
0D
0
$ E "
3 *
3
3
3 :
. "
""
"-
"
?
?
; "- "
F "
"
"
--
"
0" "-
" 0"
"
- "
.
/0
- " /
"
" 0"
- "
"
"--
4
#
0"
B
C
- "
C
G G
GG G
G
G G
.
- "
" " - "
0
; @0
"
; @0
/
EE
E E
E
EE
E
E
E
E
E
(
C
- "
" " - "
". " "
; @0
/
,
#
4
2"
&
!
&
&
&
&%
"
%
%&
& %&
&
"
&
&
%&
%&
&
%&
&
%
&
%&
&
%&
&
%&
& % %'
& %&
( )
0
%&
&
&
%&
%
&
&%
+ ()
"
"
+ (&
*
!
%
%
&'
%
,
. "
- "
+ ()
/
,
+ (&
. "
" - "
#
( )
#
1
/
&)
+ (&
%&
%
&'
%
" - "
+
()
,
%
- "
%
&)
*
+ ()
"
#
5
3 2" 0
3 (
3 *
$:
0
- "4
"
"
" 0
0 4
"
9
4#
4
$:
"
" 0
4
$:
3 2
" 9
3 E
"
"
0
"
0
"
0
0
4#
0
0
0
4 *
"
+ (&
0
#
3
"0
3
"
"
"
$ + "
$ ! "
$
"
" "
"
0
"
"
"
"
"
0
"-
" "
"
; (
""
"
*
#
6
2"
16
"
,
"
0
L
14
4'
.∆ IJ/ K
12
10
8
*
"-
6
4
2
0
#
0
#
'
,
,
- "
- " 4
"
0
-0
" 4
'
C
0
; "
- "
#
"
; (
6
7
C
3
- "
"@0
- "9
*
"
%
"
C %&
)
C %
*
%
)
(
%
"
%
&
%
C
0
%
% &
%
%
& &
%
% &
C
%
%&
& &
#
<
C
3
- "
"@0
'
2
- "9
-- - "
& %&
&
%
2
%
%&
C
6
(
C
- "
E"
&
&
%&
<
)
&
&
& %
&
"
C
C
%
&%
&
&
%&
&
%
CJ
%
)
&%
&
&
CJ
#
#
8
,
- "
3:
"
0
4#
- "
0
"
#
0
--
"
0
3! "
#
"
" 0
"
*
0
-0
#
B
& %&
%
%&
0
%&
*
%&
%&
%
%'
))
$
%
&
%
0
(
%&
#
%&
%&
%&
%
%'
, 0
!
&
&
& %&
%
#
%&
*
%&
%&
%
%'
, 0
&
%
4#
%
%
&
%'
%&
(
%&
%&
#
&
&%
%
4'
%
%'
%'
&
%
%'
%&
%
(
!
&
%&
"
&
%
+ () )
'
%
+ (&
% %'
(
!
))
%
*
%
%'
!
%
&'
&%
&
Mg++, K+
%
% %'
$
0
*
,
%
"
%&
%
%
'
%
%
(
&
&
% %'
))
%
%
&
%
0
#
9
,
,
- "
0
4#
& %&
%
%&
0
%&
*
%&
%&
%
%'
))
$
%
&
%
0
(
%&
#
%&
%&
%&
%
%'
, 0
!
&
&
& %&
%
#
%&
*
%&
%&
%
%'
, 0
%
%
&
%
%'
&
4#
%&
(
%&
%&
#
&
%
4'
%
%'
%'
&
&%
%
(
!
%
%'
%&
&
%&
"
&
%
+ () )
'
%
+ (&
!
% %'
(
))
%
*
%
%'
!
%
&'
&%
&
Mg++, K+
$
%
% %'
%
*
0
,
%
"
&
%
%
'
%
%
(
&
%&
% %'
))
%
&
%
0
#
M
,
& %&
- "
4#
0
3
"0
%&
&
"
"
.
:= )
:=
%&
%&
"
))
E
.E
B
/
& % %'
/
%
&
0
#
&
&
%&
&
&
%&
9
* → ,G )
"
(
%&
"
&
&
*
0
0"
3 C 0
&
%&
0
"
"
%
&
#
%&
,
(
0
& % %'
%
, 0
#
&
.E
<'
M/
& %&
&
%&
%&
&
,#
%&
*
))
,
0
"
.E
B
/
(
& % %'
%
, 0
4#
&
& % %'
&
%&
%&
&
%&
,G
#
10
& %&
%
%&
0
*
%&
%&
%&
%
%'
))
$
2*% (2
CE %: W2%+E
%
&
%
0
(
%&
#
%&
%&
%&
%
%'
, 0
!
&
#
&
& %&
%
%&
*
%&
%&
%
%'
, 0
&
%
&
4#
2*% (2
CE %: W2%+E
%
%
%'
%&
(
%&
%&
#
%
&
4'
%
%'
%'
&
&
%&
%
%&
"
&
%
+ () )
'
%
+ (&
!
% %'
(
))
%
2*% (2
CE %: W2%+E
*
%
%'
!
%
&'
%
%'
&%
(
!
&%
&
Mg++, K+
$
%
% %'
&
&
%&
&
%
% %'
%
))
%
%
*
0
,
'
%
%
(
%
"
%
0
#
M
%
"
2"
45
(
3 2"
"
0
"-
"
$ C 0- "
$
C
"
+ ()
" "0
0- "
- "
$
- "
"
0- "
3 2"
"-
"
$ (
- " 4
$
1
$ C
- "
4
0
#
M
(
3 2"
"
"-
$+
3C
0
"
0
C
"
)
+ (
" "0
:
$+
3(
@0 "
#
"
M
46
"
0
&
"
&
&
&
&%
%
!
%&
& %&
&
%&
&
&
&
%&
%&
&
&
%&
%&
"
&
%
&
%&
&
%&
&
%&
& % %'
& %&
( )
0
%
&
&%
+ ()
"
"
+ (&
*
!
%
%
&'
%
%
,
. "
+ ()
/
,
+ (&
#
" - "
. "
( )
#
1
/
&)
+ (&
%&
%
&'
- "
" - "
+ ()
,
%
- "
&)
*
%
+ ()
"
#
M'
"
(
'
"
&
%
%'
%
%'
&
%&
&%
!
%
&
%
4'
%'
%
&
%&
+
+ (&
0
+ ()
% %'
%
(
:
!
))
%
&'
%&
*
'
%'
%&
!
!
,
"
%
&'
#
%
(
%
%
0
&%
&
$
% %'
*
&
&
Mg++, K+
%
%
&
%
%
0
%
%
%
% %'
))
%
%
M6
47
"
(
'
"
&
%
%'
%
%'
&
%&
&%
!
%
&
%
4'
%
%'
&
&'
%&
E "
+
+ ()
%&
&
+ (&
% %'
%
(
#
!
!
&
*
'
&'
))
%
%'
%
&
%
%&
!
%
,
0
"
%
&'
*
(
%
&%
&
$
% %'
%
%
0
&
Mg++, K+
%
%
&
%
% %'
))
%
%
%
#
MM
0
E
3
--
6
- "
0
3 =
"
"+&
+
&'
)
+
+
&'
&
%
%
%
2(%
%
%
%
%
2(%
#
50
E"
0
,
.KV
0
"
E
/
"
"
"
'
"
E"
.∆ I;/
.∆ /
0
E"
:
"
0
2"
,
*
'
6
'
6
<
#
B
M
#
M
E"
/
'
.KV
"
.∆ I;/
.∆ /
E"
:
2"
'
6
'
6
<
#
B
M
#
55
E"
S 6' 6 KV
∆
#&
%# ) #%
∆ S
<
3:
0 -"
"
# % ) #& %
KV
0
BX
0
0
"
"0
#
Gli enzimi glicolitici possono formare
complessi multiezimatici
3 +
0
0
"
3 E
- "
"
- " " "
"
0
"
0
0
;
"
"-
"
"
"" 0"
"" -"
0" "0- "
#
56
-0
"
%
%&
%&
&%
" "
& %&
%&
,C=**% %
%&
%&
&%
9
& %&
%
%&
& %&
%
%&
%&
&%
: **% %
&%
%
%&
%&
%&
%&
%&
& %&
%
%&
%
&%
++% %
&%
%& %&
%&
%&
%&
%&
#
'
0
, 0
.
, 0
(
*
%
&%
&%
, 0
%
%
%&
%&
%
, 0
.E
%&
/
& % %'
&%
"
B
%
%&
'/
&%
%
%
%&
&%
&
&
%&
&
%&
& %&
*
, 0
&
'
(
%
%
&%
%&
%
%&
, 0
%&
&%
%&
&
%
&
%&
.E
"
B
.E
%
/
%&
.E
*
%
%
%&
%&
)
'/
%&
&%
+ (&
(
%&
6
"
/
%&
+ ()
*
%&
#
.E
B
"
' /
(
%
%
'
%
.E
%
(
:2 %:2 2
"
%
#/
%
%& %
"
&%
+ ()
%
%
+ (&
'
#
6
57
0
, 0
.
, 0
(
*
%
&%
%
, 0
.E
%&
%
%
%&
%&
&%
/
& % %'
, 0
&%
"
B
%
%&
&%
%
%
'/
%&
&%
&
&
%&
&
%&
& %&
*
, 0
&
'
(
%
%
%&
%
&
%&
%&
%
&%
&
%&
&%
, 0
.E
"
B
.E
%
/
%&
.E
*
%
%
%&
%&
)
%&
%&
'/
%&
&%
+ (&
(
6
"
/
%&
+ ()
*
%&
#
.E
"
' /
B
(
%
%
'
%
"
%
.E
%
(
#/
%
%& %
"
%
&%
+ ()
:2 %:2 2
%
+ (&
'
#
B
"
.") 0" ?/
"
." 0" ?/
=(
& %&
& %&
%
%
%&
&%
&%
(
*
%
%
%
&%
&%
%&
.E
%&
"
%&
&%
%
%&
&%
&%
"
B #/
%
%
%
%&
%&
%
%
&%
%&
&%
")
%&
%
%
%
%
%
&%
%
+
+&
%
&%
%&
%
=(
0
%&
%&
0
.E
"
BB
=(
6
.E
/
<
'
/
%
&+
,
%
%
%
%&
%
%
&%
%&
.E
0
<6
%
0
/
%
&%
&%
#
%&
%&
%
%
%
%
%&
0
%
%
%
%
&%
%
&%
%
%
+
%
%
=(
%&
%&
&%
%&
0
:2 %:2 2
#
59
""
""
%
%&
""
(
*
%
&%
%
%
&%
%&
%&
E
.E
"
B
#
%&
%
%
&%
/
%&
%&
,
.E
""
<'
/
%
%
:2 %:2 2
%&
%&
%
%
%
&%
, 0
%&
#
#
M
0
"
"
0
"
0
2"
60
0
3 :
0
3 :
"
"
"
"
"
"
"
0
"
0
"
0
0"
"3 *
- "
" "
"
ZE
Z,
Z 0
3 >0
0 "
"" 0"
∆
"
- "
9
"
0
"
"
"
"
"
#
G
3 :
0
0
- " 9
"
&
,
3 :;
3 E
.
-% %'
"
(
%
%
%
*
0
0"
;
"
∆
."
/
0"
--
;
0 +*
&'
0
E
; *
"
"
M g++, K +
%
%
3 2 ∆
" 0
"
4
0
*
A
E
"
*
*
/
#
61
0
"
"
& %&
%
%&
*
%&
%&
%
%'
))
$
&
%'
, 0
$
0
&
%'
&
"
*
%
&
%
!
, 0
%
%'
%&
"
%
'
#
% %'
%
&
%'
&
%
%'
%'
%
!
%'
%&
#
&
%&
%&
%&
%&
$
%
'
%
%&
0
%
%
0 0 01
& %&
%
%
% %'
))
&
%
0
&
$
0 0 0
%&
&
&
$
%'
%&
(
%
%
&
))
%
!
&%
"
%
& %&
%
%&
% %'
%
+ (&
&
%
%
%&
*
,
+ (&
%&
4#
, 0
!
(
&
4'
%
&
&
&
+ () )
&
%
*
%&
& % %'
*
%&
%'
%&
%
%
%&
&
%
0
%
#
4'
%
%'
% %'
&
(
%
%&
(
&%
%
!
+ () )
'
%'
%
%'
%
& %&
!
#
%
Mg++, K+
% %'
$
&
%
%'
%&
&'
%
&%
%&
(
%
!
%
%&
%'
0
% %'
&
(
&
%
4#
%
%
$
%
$ /0 0 0 1 2 . 3
$ /0 0 0 4 2
3
$ /0 0 0/1 2#. 3
%
%&
%&
&
%
0/0 0
& %&
%
#
%
"
'
!
%&
, 0
*
%&
%&
%
,
%
(
%
%
&'
(
%&
%
%
%
%
%&
#
(
*
%
%
%
0
%
& %'
%&
0
%&
%&
0
%&
#
'B
0
"
"
& %&
%
%&
*
%&
%&
%
%'
))
$
&
%
%'
$
0
(
(
"
%
&
4#
%'
!
, 0
%
%'
%&
%
&
%
+
()
%
+ (&
!
&%
&
$
,
%
"
0
%
%
%'
%
&
%'
%&
&
& %&
%
%&
#
%
&
%
$
%'
%&
%
%'
!
&
%
0
%&
#
&
%&
%&
%&
%&
$
&
%
%
0 0 0
%&
&
0 0 01
& %&
%
%
'
%
%
(
%
&
&
(
% %'
))
#
%
))
%'
*
%&
4#
% %'
%
*
%
% %'
%&
, 0
!
0
%
&
!
&
)
'
% %'
+ (&
%&
%'
%&
%
%&
& % %'
*
%&
&
"
%
Mg++, K+
%
(
%
4'
4'
%
%'
&%
%
%
%'
%'
&
%
(
#
&'
!
&
%'
#
%&
(
& %&
%
&
%
%&
%
% %'
&
&%
%&
&
%
$
+ () )
'
%
*
%&
%
%
%
!
%&
, 0
%
0/0 0
0
% %'
$
%
$ /0 0 0 1 2 . 3
$ /0 0 0 4 2
3
$ /0 0 0/1 2#. 3
& %&
%
&
%
&
%&
%'
"
'
!
&
#
%
*
%&
%&
, 0
,
%
(
%
%
&'
%&
%
%
%
%
%&
#
(
*
%
%
%
0
%
& %'
%&
0
%&
0
%&
%&
%&
'
69
0
3 :
0
"
"
"
0
"
0" 7
"
"
"
"
3
"
"-
"
"
0
0
8
"
+ () )
( )
) + (& )
*
" 0
"
3
9
0
3
0
"
)
0
"
9
) + (& )
) + () ) 6
0
0
3
)
0 "
* )
"
6 * )
*
( )
( )#
9
*
( )
( )6
#
'M
0
3
"
"
"
"
"
:
"
"
0
"
"
9
$ C
"
"
:
9
:
0
3 >0 "
*
3 2" @0
3 >0 "
. " "
"
#
9
"
0
3
"
"0
0
"
4#
"
/
"
/A "
.
- "
0
.
0
* A
+%+ A
*
"
"
.
/A "
"
" - "
0
0 0
" " - "
* A
- "
/
0 +%+
"
-0
"
- "
0
"
"
6
70
0
3
"
$ +
"
"
"
9
A ;
4
0
%+E @0 "
;
:=
$ :
(
"
"
" /
"
"
0
0
;
A
0
.
"
0
"
A
"
"
- "
A9
0
"-
- "
- "
$
9
D
0 "
?
"
"
4
0
"
" 0
#
6
0
3
"
"
"
9
"
9
$
""
" ,% ,%C2: *2
"
" 9
0
@0 "
"
9 "-
CEG .
"
0
"
:; "-
A "
"
"
E
0
"
- "
9
"
"
"
" "
4
"
"/9
- "
"
0 "
- "
0
4#
#
6
71
"
"
"
"
2"
" .
3 2
3 2
" A 0"
"
"
α →# "
0 0 - "
"
"
3 E 0"
"
& %&
& %&
%
%
α→6 "
"
- "
0
"0
"
%
%&
%
"
%&
%&
%&
& %&
%
%
%
"
%&
# &
%
& %&
%
6
α
%&
%
µ
%
& %&
%&
α
%
& %&
%&
#
4
& %&
%&
&%
%&
0
"
%&
&%
/
%&
%
%&
%&
%
%
%&
& %&
%
%&
%
%&
%&
%&
6
74
" .
3 2
3 2
"
"
3 E 0"
"
"
" A 0"
"
"
α →# "
0 0 - "
"
& %&
& %&
%
%
%&
α→6 "
"
%&
0
%
%&
%&
& %&
%
%
%
%&
"
# &
& %&
%
6
α
%&
%
"0
α
%
& %&
%&
"
- "
%
& %&
&%
4
%&
%
%&
0
& %&
%&
&%
/
%
%&
%&
%
%&
%
%&
%
%&
& %&
%
%
%&
%&
%&
%&
#
6M
" .
3 :
0 0
-- - " .
"0
"
0"
" /
"
"
[
?
& %&
& %&
%
%
%&
& %&
%
%&
&%
%&
%
"
%&
%
%&
%&
& %&
& %&
%
%
%
%&
&%
"
%&
#
%
&
& %&
%
6
α
%&
%
%&
α
%
& %&
%&
#
/
%&
%
%&
%&
%
%
%&
& %&
%
%&
%
%&
%&
%&
<
75
"
3 :
.
"
"
"
0
"
& %&
.E
& %&
%
E
"
C
%&
%
%&
% %'
%
&%
%
CJ
C
%
)
%&
"
&%
C
%
%&
%&
%
%
C
%
&%
%
%&
%&
%
,
)
&%
& %&
%
%
%&
%
& %&
& %&
6
%&
%
%&
"
/9
"
%
%&
&%
6
& %&
%
%&
"
/
%
%
)
CJ
&
%
%
2
3 (
C
CJ
%
"
α→6
C
)
&%
&
"
"
&
%
)
&
CJ
%
; "@0
0
α→#
#
<
"
#
E
6
<
76
3
0
- "
3 ! "
"
0
"
;
"
(
"
--
0
--
0
.E
*
BB
B/
(
"
"
"
+&
%
%
%
%
%
%
+
O
%
%
%
+
%
%
%
HO
+
)
+
HO
HO
%&
&%
(
%
O
%
OH
0
E
BB
B
+&
%
%
%
%
%
%
%
%
HO
+
+
O
%
)
HO
%
O
%
HO
%
+
%
%
+
OH
%&
&%
#
B
"
3 2
"
"" 4
0"
0"
@0
0
0
#/. 0
3 :; ".E
6
%
HO
O
HO
%
"
0
%
4
0
"
A
""
- " /
C
%
&%
O
HO
"
%
%
%
%
+
%
)
+&
OH
&%
%&
%
+
&
C
OH HO
%
%
%
HO
%
%
%
%
%
%
&%
+
%&
+&
O
)
HO
C
O
%
%
+
#
C
&
B
86
"
3 2
"
0
. "
0
"
"
0/
"@0
0"
"
#
B'
"
3 2
"
0
. "
0
"
"
0/
"@0
0"
"
OH HO
HO
%
HO
%
O
O
HO
O
HO
%
%
%
%
%
HO
%
C
O
+
)
+&
OH
&%
%&
%
%
+
7/
&
!
0/0 0 4
$
C
HO
C
HO
%
%
%
)
%
%
%
&%
#
%
%
%
+
%&
+&
%
HO
O
&
+
O
HO
O
C
OH
HO
O
OH
/
%
B6
87
"
3 2
0
$+
$+
"
0
0
9
"
"
9
0
*
" "
.
0
0
-- "
0
"
/
3 :
"
- "
" @0 "
"
"
0
"
#
"
"
=(
0
%
HO
O
HO
O
HO
=(
%
%
%
%
%
%
%
%
%
+
&%
%&
+
&%
+&
& %&
%
"
%&
)
" /"
%&
%
%&
.
"
C
%
%&
%&
)
" /")
"
% %'
%
%&
&%
%&
.
%&
%
& %&
%
%&
C
%
& %&
%
%&
&%
%&
)
& %&
%
%
%
%
"
& %&
&%
%
%
"
%
%&
& %&
%
%
+&
OH
)
%
%
%
&%
%&
%
0
3
"
"
"
" " 4
"
0
"
"
"
3
"
"
"
0
.
@0
"0
"
?
"
- "
"
=(
0
"
"
"
0"
/
- "
#
91
C
- "
3 : !
0
"
!
3
.
0
3
"
#
@0
0
#
"
4
3 >0 "
4
"
A
*
"
/
4
"
0
0
"
"
!
"
A
-- "
"
" A "
- "
*
"
;
"
- " *
@0 "
0
0
"
3 >0 "
"
#
#
.
/
"
A
0"
0
0
A
"-
" @0 "
; *
" /
" "
"
- " C
*
3 : !
0
.0"
"
@0 "
0"
0
#
#
'
C
3 2
- "
0
#
0D "
"
."
0
"
3 2" @0
/
#
" 0
0
0
"
@0
"-
"
& %&
& %&
%
& %&
%
%&
%&
%&
%
%
%&
%&
& %&
& %&
&
%
%
%&
%&
%&
%
%&
E
%
%&
%
%&
%
%
%&
& %&
%
%&
%
%&
& %&
%&
& %&
%
%&
&%
"
%
%&
%
"
& %&
%
%&
%
&%
&%
%&
%&
%&
%&
"
0
"
0
0
& %&
"
& % %'
%
%&
%
%&
&%
#
& %&
%
% %'
0
%&
&%
%&
%&
&%
%&
%&
0
)
& %'
%&
#
0
(
*
ER
0
%
%
:2 %:2 2
%
&'
0
#
6
92
"
*
+ ( &
α (
0
β (
#
%
#
%
%
%
%
%&
%&
.E
3 E"
"
,
0
.E
( R 0
(
<
0
%
"
6M/
%
"
%
%
C 0
'
.E <
%
0- "
"
"
66/
#
,#
%
"
&%
&%
%
.E
%
%&
<'
%&
&%
#/
(
<
/
%
%
)
%&
%
&%
%&
%
%&
'
%
%
(
0
B
%&
%
%
(
%
* "
.E
* "
.E
"
%&
* "
.E
"
%
<
%&
:2 %:2 2
0
%
C
%
%&
(
%
%
%&
&
0 "
"
'
' /
%
%
/
%&
*
$ ! "
"
+ ( &
.E
#
%&
,#
%
%&
%&
&%
%
%
'
%
&%
%&
%
<
%
"
&%
%
#
4<
#
.E
%
%
"
%
%
0
%&
'
0
"
%
%&
&%
M/
0
%
,#
#
<'
(
"
&%
0
&%
#
,#
%
%
%
&%
$ :
0
%
%
%
/
%
/
"
"
%&
)
%&
%
"
"
"
%
!
%
*
(
%
6
#
''
%
#
"
"
2"
117
&
"
!
%
%&
& %&
&
&
%&
"
%
%&
&%
&
&
%&
&
&
%&
&
%
&
%&
%&
&
%&
&
%&
& % %'
& %&
( )
0
&
&
&
&
&%
+ ()
"
"
+ (&
*
!
%
%
&'
%
,
. "
- "
+ ()
/
,
+ (&
. "
"
- "
#
( )
#
1
/
&)
+ (&
%&
%
&'
%
" - "
+ ()
%
,
- "
%
&)
*
+ ()
"
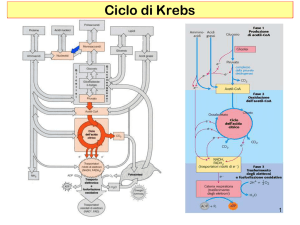
• In condizioni aerobiche il piruvato prodotto
dalla glicolisi e dalla degradazione degli
aminoacidi è ossidato a H2O e CO2 nella
respirazione cellulare.
• Ciò avviene in tre stadi
– Produzione di acetil-CoA (decarbossilazione del
piruvato)
– Ossidazione dell’acetil-CoA a CO2 (Ciclo di Krebs)
– Trasferimento di elettroni e fosforilazione
ossidativa (produzione di H2O e ATP con
consumo di O2 ).
#
'#
118
#
'B
0
"
Produzione di acetil-CoA
(decarbossilazione del piruvato)
119
*
3 2
0
0
A
;"
"
"
"
"-
0
"
3 2
0
"
"
"
0"
"
%&
3 :
"
.!(
"
"
9
"
"
"
" "
"
"
"
"
#
" "
"
""
"
/
'M
"
#
6
120
"
,
"*
"
,
"
# *"
"
,
"
"
,"
,
β &
(
,
,
&
"
"
#
#
#
"
"
,
*
"
,
"
;
"
"
,
"
,"
,
,
"
,
"
#
#
#
6
# *"
#
β &
(
&
#
(
#
<
#
#
#
6
121
0
&(
3 2
0
" "
- "
"
"
"
"
0
A 0" 0
-- "
- "
"-
3 :
- "
"
"
" + (&
"
0"
" &
+ ()
3 2 + (&
"
"
3 :
- "
0" ∆ I; S '' 6 KVL
.
"/
+ ()
"
+ (&
&
*
"
&(
4:
(
2$
)
4, (
"
!
$
$ 3
#
6'
0
&(
"
• Il complesso piruvato deidrogenasi catalizza
cinque reazioni sequenziali, richiede tre
enzimi e cinque coenzimi.
• I cinque coenzimi sono:
3
3
3
3
2 #
: .
2 (
2
#A
"
"
,#
"
0
A
"
4
0
"
0"
"
#
66
122
2
"
, (
&
+ ()
&
(
2
*
!
$
:
%&
%
, (
C
(
&
$
%
C
%
*
&'
%
&'
&
(
!
$
%
+ (&
*
&'
%
&'
&
&
C
#
6<
:
"@0
- " "
&(
, (
&
+ ()
&
<
(
2
*
!
$
:
%&
%
6
*
&'
C
%
C
%
*
&'
(
&
$
%
+ (&
&
(
!
$
%
, (
'
&'
&'
%
&
&
C
#
6#
123
"
0
&'
"
%
%
%
%&
*.
&'
&
$' '
&
*
&'
$
&
&'
, (
*
$
&'
&
%
$'
$
&'
, (
$
+ (& ) &)
&'
%
+ ()
&
*
*
&
$'
&'
$
&'
, (&
$
&'
$
&'
&'
$
&
&
*
, (
$
&
&'
&'
$
&
$'
$
, (
%
&'
#
BM
1
.*
/
;
Ossidazione dell’acetil-CoA a CO2
2"
140
1
+
:
"
""
M<'
#
1
• Il ciclo di Krebs è al centro del
metabolismo.
• Le vie degradative (catabolismo) lo
alimentano, le vie sintetiche
(anabolismo) ne usano i componenti.
• È una via “ANFIBOLICA”, opera infatti
sia nel catabolismo che nell’anabolismo
cellulare.
#
141
1
• Tutte le reazioni avvengono nella matrice
mitocondriale.
• Nei mitocondri vi sono anche gli enzimi della
fosforilazione ossidativa e quelli della ossidazione
degli acidi grassi e degli aminoacidi.
AcetilCoA + 3 NAD+ + FAD + GDP + Pi + 2H2O
2CO2 + CoASH + 3 NADH + FADH2 + GTP + 2H+
#
'
1
" V
"
#
"
" . M'B/ 7*
" "
69 6
<#
"
0
8
6
142
1
%
+ (& ) &)
+ ()
&'
%&
%
%
%
0
%
%
%
%
&'
&
%
& %
%
%
%
%
%
%
&
%
%
%
%
%
%&
%
%
,0
%
%
& %
%
, (&
%
%
%
, (
%
"
%
%
%
&
0
%
"
%
%
& %
&
0
*
%
"
%
%
%
%
2
( )
%
0
α
%
%
&
%
0
"
%
%
%
&
%
%
+ ()
+ (& ) &)
+ (& ) &)
%
+
&%
%
%
()
%
%
%
%
%
%
%
#
<
1
%
+ (& ) &)
+ ()
%
&'
%
%
%
%
0
%
%
%
%
%
%
&'
&
%
%&
%
%
& %
%
&
%
%
%
%
%&
%
%
,0
%
%
& %
%
, (&
%
, (
%
%
"
%
%
%
%
&
0
%
"
%
%
& %
&
*
#
*
%
2
( )
*
&%
&
#
%
1 :
%
%
0
α
%
%
%
&
%
%
+ ()
+ (& ) &)
+ (& ) &)
+ ()
%
%
%
%
#
#
143
1
,# "
#
"
%
#
#
,#
%
&
*
"
%
%
%
%
&'
# *"
& %
%&
%
%
%
%
%
%
%
%&
%
%
%
%
& %
%
E@0
# "
#
+0
%
"
"
0
%
%
%
%
%
%
&
%
%
%
&%
# *"
.
%
%
%
%
%
%
%
&%
# *"
%
%
%
%
,# "
%
"
,#
,# "
%
,#
%
%
%
&
%
%
"
%
%
%
%
#
B
1
+ (& )
+ ()
%
&)
&'
%&
%
%
%
%
%
$
!
0 0 0 :
$
&
/0 0 0
$
%
5
%
%
&'
&
%
& %
%
%
%
%
%
&
%
%
%
%
0 0 0
%
%&
%
%
%
%
, (&
%
%
%
!
0 0 0
$
%
& %
#
$ /0 0 0
*
, (
%
%
%
&
*
%
&
%
*
%
#
$
%
%
#
$ /0 0 0
0 0 0/
%
α
( )
!
!
0 0/0
$
%
%
%
%
!
0 0 0/
$
&%
%
%
%
+ ()
+ (& ) &)
+ (& ) &)
%
+
%
%
%
&
%
%
()
%
+
&
%
& %
%
%
%
%
%
%
#
144
1
%
+ (& ) &)
+ ()
&'
%&
%
%
%
%
%
$
!
0 0 0 :
$
&
/0 0 0
$
%
5
%
%
&'
&
%
& %
%
%
%
%
%
&
%
%
%
%
0 0 0
%&
%
%
%
%
%
, (&
, (
(
%
*
%
*
%
%
"
%
&
%
#
$ /0 0 0
0 0 0/
%
α
( )
%
%
#
$
&
%
%
%
!
0 0 0
$
%
& %
#
$ /0 0 0
*
!
!
0 0/0
$
%
%
%
!
0 0 0/
$
%
%
&
%
%
+ ()
+ (& ) &)
+ (& ) &)
%
%
%
%
&%
%
%
+ ()
%
+
&
%
& %
%
%
%
%
%
%
#
M
1
+ (& )
+ ()
%
&)
&'
%&
%
%
%
%
& %
#
$ /0 0 0
%
%
%
%
%
*
%
%
%&
#
!
0 0 0
$
%
%
0 0 0
B
*
, (
%
%
$
%
%
, (&
%
%
!
0 0 0 :
$
&
/0 0 0
$
%
5
%
%
&'
&
%
& %
%
%
%
%
%
&
%
%
&
%
*
%
#
$
%
%
α
( )
%
6
0 0 0/
%
%
%
%
!
0 0 0/
$
&%
%
%
+ ()
+ (& ) &)
%
%
%
%
&
%
%
+ (& ) &)
+
%
+
%
()
& %
%
&
%
#
$ /0 0 0
'
!
!
0 0/0
$
%
&
<
%
%
%
%
%
#
M
145
1
%
+ (& ) &)
+ ()
&'
%&
%
%
%
%
&'
&
%
& %
%
%
%
%
%
&
%
%
%
%
%
%
%
%
%&
%
B
%
%
%
& %
%
, (&
, (
#
%
%
%
%
%
%
%
&
%
%
%
'
<
*
& %
%
%
%
%
%
( )
%
%
&%
&
%
%
%
%
%
+ ()
+ (& ) &)
6
+ (& ) &)
%
+ ()
%
%
%
&
%
%
%
%
%
%
%
#
M
1
:2 E+* W2%+E
C2 C2 *2+%
2 :%
B
CE
#
E %+(%
%
C%(=W2%+E
E+EC 2 <
6
#
C W2%+E
2 :%
'
C2 %
%
C%(=W2%+E
E+EC 2
M
146
"
.E
#
+ (& ) &)
#
+ ()
%
''
#
%
&
*
"
%
%
%
&'
# *"
/
%
& %
%&
5
%
%
%
%
%
!
0 0 0 :
$
&
$ /0 0 0
$
0 0 0
"
%
, (&
&%
#
$ /0 0 0
*
, (
$
%
%
%
!
0 0 0
%
%
%
%
&
*
%
&$
%
*
%
%
#
#
$ /0 0 0
0 0 0/
%
%
α
( )
!
!
0 0/0
$
%
%
+
%
%
!
0 0 0/
$
&
%
&%
%
%
%
+ ()
+ (& ) &)
+ (& ) &)
%
%
%
%
&
%
%
+ ()
&%
%
%
%
%
%
%
%
#
M'
"
.E
#
+ (& ) &)
+ ()
%
''
#
#
%
&
*
"
%
%
%
&'
# *"
/
%
& %
%&
5
%
%
%
%
%
!
0 0 0 :
$
&
$ /0 0 0
$
0 0 0
"
%
, (&
&%
#
$ /0 0 0
*
, (
!
0 0 0
$
%
%
%
%
%
%
%
&
*
%
&$
%
*
3 >0 "
3
3 :;
%
%
#
#
$ /0 0 0
0 0 0/
%
%
α
( )
!
!
0 0/0
$
%
%
+
%
%
!
0 0 0/
$
&
%
4
%
&%
%
" "A
F
%
%
- " 4
%
%
+ ()
+ (& ) &)
%
%
%
%
"
&
%
%
+ (& ) &)
+ ()
&%
%
%
;
@0
%
%
#
M6
147
"
.E
6
%
+ (& ) &)
3
--
"
"
%
+ ()
%
%
- "
%
%
$
%
"
"
&
%
$
- " 4
0 0 0
"
" "A
"
#
$ /0 0 0
,
0 0 0
*
&
%
( )
%
#
%
*
&'
%
%
" ,
3 2 ∆
%
4
A! 0" 0
%
*
%
%
!
0 0 0 :
$
&
$ /0 0 0
, (
6 6/
&'
5
"
, (&
0"
%&
%
%
"
%
0"
%
$ :; "
$ +
.,
$ *
0"
&
%
%
& %
'/
$
0
%
"
"
#
4 0 0 0/@0
%
α
!
!
0 0/0
- " A$
#
$ /0 0 0
4
&
%
"
%
!
0 0 0/
$
%
%
"
+ ()
+ (& ) &)
%
%
%
%
%
%
"
%
%
+ (& ) &)
+ ()
"
+
+
4 ∆
" - "
%
-
A
%
%
#
'
"
.E
6
'/
,
,
,
,
#
'
151
2
"
.E
%
+ (& ) &)
3
3 :
6 /
&
-- "
- " "
"
+ () .
+ (
"/
0 5 %&
" 4
$
0 0 0
!
$
0 0 0 :
3
;"
0 "
"
@0
&
$ /0 0 0
)) . "))/4
_"
- "
"
"
#
3 2
0
%% "* " "
"
- "
$ /0 0 0
!
%
4
$
0 0 0
3
α−
0
+ ()
%
%
%
&'
%
&'
&
%&
%
%
4
" 0"
%
%
%
& %
)
%
%
%
%
%
%
%
%
%
A
%&
%
%
%
%
& %
%
, (&
%
, (
%
%
%
%
%
&
*
%
&
%
*
$
%
%
#
$ /0 0 0
0 0 0/
%
α
( )
$
%
%
#
!
!
0 0/0
!
α %
%
+
$
!
0 0 0/
+
"
&
%
& %
"
,#
,# "
+ (& ) &)
+ ()
"
5!
#
' M
2
"
3 :
- " A
- "
" " .∆ I; S
%
%
%
%
6 /
%
+ (& ) &)
"
%
%
"
4
&
%
%
%
@0
- "
"
M
KVL
/
5
$
0 0 0
!
$
0 0A
0 :
"
9
&
$ /0 0 0
"
( . *
"
"
))
)
#
+ ( .+ (& $"/0 0 0 "
/
!
* L ( A
1
0 0 0
& %
3 :;
$
$
$ >0 "
A
"
+ ()
.E
&'
%
&
%
%&
%
%
&'
%
%
%
%
%
%
%&
%
%
%
, (&
*
%
, (
$
%
%
%
%
%
%
&
*
%
&
%
*
%
/
& %
%
$
%
%
#
#
$ /0 0 0
0 0 0/
!
!
$
0 0/0
!
α %
& %
%
α
( )
%
%
+
$
!
0 0 0/
+
"
&
"
,#
,# "
+ (& ) &)
+ ()
"
5!
#
'
155
0
α
"
3 E 0"
0 "
3 :
- "
+ ()
%
%
"
%
;α
%&
"
%
; "
%
5
$
, (
E'
%
%&
/
%
%
0
%
& %
%
"
%
"0!0
$
"
0
&
%
%
%
%
"-
4
%
0
%
&
%
#
$
#
$ /0 0 0
0 0 0/
#
α %
!
!
$
0 0/0
*
*
( )
α %
# *"
*
/0 0 0
0
?
%
*
%
%
"
, (&
$ E
$ E
0
%
%
0 0 0
- " A
"$ &/0"0 0 .∆ I; S '' < KVL
"
@0
"
@0
#
"
.E 4* E 4 E'/
$
%
& %
%
%
%
+
!
%
!
0 0 0/
$
&%
%
&
%
#
%
%
%
,# "
/
%
%
$
!
0 0 0 :
6
&'
&
%
%
%
&
&'
& %
%
%
%
%
%
3 :
3
+ (& ) &)
"%
0 + (&
.E
"
+ ()
+ (& ) &)
%
,#
%
%
%
%
#
' '
0
"
"
.E
%
+ (& ) &)
+ ()
%
&
%
%
&'
%
%&
%
%
%
%
%
$
!
0 0 0 :
$
&
/0 0 0
$
%
5
%
%
&'
&
%
%
%
6/
%
& %
%
#
%
0 0 0
%
%&
%
%
%
, (&
%
$
& %
#
$ /0 0 0
*
, (
%
!
0 0 0
%
*
#
$
# *"
α
%
#
$ /0 0 0
0 0 0/
*
& %
#
%
$
!
!
0 0/0
%
+
%
!
0 0 0/
$
&%
%
#
%
%
%
+ ()
+ (& ) &)
+ (& ) &)
%
+ ()
%
%
%
&
%
%
%
%
%
&
*
%
&
*
.
%
%
%
%
%
%
%
#
' 6
157
0
"
"
.E
%
+ (& ) &)
+ ()
%
3
%
%
$
&
/0 0 0
$
&'
%
&
%
%
"
0
%
"
"
*
. * /
$
0 0 0
!
0 0 0 :
( . ( /
3 :; "A
" 0" &
#
3 E 0"
9
$ /0 0 0
$ : 0 0" ? α " "
- " .& /
%
5
%
6/
%
&'
%
%&
%
&
%
%
& %
%
#
0
%
%
%
"
0
%&
%
%
%
%
& %
%
, (&
*
%
, (
!
0 0 0
$
%
%
%
*
%
&
*
#
$
# *"
$ :
0 0" ? β ?
*
*
+
!
3 : $ 0 0 0/- " A
"
.∆ I;S M KVL
/
#
%
α
$
%
&%
%
%
%
+ ()
+ (& ) &)
+ (& ) &)
%
+
()
%
%
; @0
%
&
%
%
%
?
%
%
#
& %
%
%
!
!
0 0/0
&
*
#
$ /0 0 0
0 0 0/
*
.
%
%
%
%
%
%
#
' <
"
%
%
%
%
%
)
%
%
%
%
&
%
%
%
%
%
%
9+
%
%
%
%
%
%
%
*
%
)
%
+
%
+&
#
E"%
%
%
*
%
%
)
+
+&
+&
.
%
%
+&
+
%&
&%
%
%
+
%
%
%
%
%
+
%
%
E"&%
%
+
%&
+
+&
+&
#
' #
158
0
"
"
3
0
"
3 2 0
"
'<
%
%
"
/
"
"
A
"
0
"
"
0 "
, (&
3 : 0 "
"
"
"
"
"
3
.E
"
"
0
A
0"
3 2 , (& A
"
"
3 2
"
4
0 0
0 "
4 A 0"
0- "
A
1
0
"
&
, (
%
""
0
, (4
"
""
"
%
"
%
%
%
>
%
"
"
"
#
' M
,0
.E
+ (& )
+ ()
6
/
%
&)
&
%
%
&'
%
%
$
5
&
/0 0 0
%
%
0 0 0
!
0 0 0 :
$
%
%&
%
%
&
, (&
%
%
%
!
0 0 0
$
%
& %
#
$ /0 0 0
*
, (
%
%
5
$
%
&'
&
%
"
"
%
%
%
%
%
&
*
%
&
%
*
%
#
$
%
%
#
$ /0 0 0
0 0 0/
%
α
( )
!
!
0 0/0
$
%
%
%
%
!
0 0 0/
$
&%
%
%
%
+ ()
+ (& ) &)
+ (& ) &)
%
+
%
%
%
&
%
%
()
%
+
&
%
& %
%
%
%
%
%
%
#
'
160
,0
.E
6
%
+ (& ) &)
+ ()
/
&
%
%
&'
%
%
$
5
&
/0 0 0
%
%
0 0 0
!
0 0 0 :
$
%&
%
%
%
&
, (&
%
%
%
!
0 0 0
$
%
& %
#
$ /0 0 0
*
, (
%
%
5
$
%
&'
&
%
"
"
%
%
%
%
• La fumarasi catalizza l’idratazione reversibile
del fumarato, si forma (S)-malato (L-malato).
• È una reazione stereospecifica, viene idratato il
doppio legame trans ma non il cis (maleato).
• Nella reazione inversa solo il L-malato è
substrato dell’enzima non l’isomero D.
%
&
*
%
&
%
*
%
#
$
%
%
#
$ /0 0 0
0 0 0/
%
α
( )
!
!
0 0/0
$
%
%
%
%
!
0 0 0/
$
&%
%
%
%
+ ()
+ (& ) &)
+ (& ) &)
%
%
%
%
&
%
%
+ ()
%
+
&
%
& %
%
%
%
%
%
%
#
'
"
%
&
%
%
%&
)
%&
&
%
&
%
&
%
&
%
%
%
%
)
&
&
&
%
%&
%
&
&
%&
&
%
&
%
5
)
%
&
%
#
'
161
"
,# "
.E
'B/
%
"
&
%
,#
&'
%
%
&'
&
%
& %
"
%
$
%
$
&
/0 0 0
%
!
0 0 0 :
$
%
%
0 0 0
5
5
%
%&
%
%
%
%
& %
#
$ /0 0 0
*
3 : :
"
!
$
0 0 0
"
"
"0 "
+ (&
*
#
#
$
0 0 0/
3 :
- " A
.∆ I;S M B KVL
/4
$ /0 0 0
#
" " - " α % !
A
.`
!
+
"
- " $ "0 0/0 "
!
$
0 0 0/
3 2"
- " 0
-"
A
"
.∆ I;S ' < KVL
0
"
;
-, (&
%
%
%
, (
%
%
%
%
&
%
%
&
%
*
%
%
%
%
%
& %
/4
( )
%
%
&%
&
%
%
%
%
%
+ ()
+ (& ) &)
%
%
/
+ (& ) &)
%
+ ()
%
&
%
%
%
%
%
%
%
#
' '
E"
'
"
0
"
,0
0
"
α
2
0
"
"
"
"
"
"
/
'
∆ IJ .KVL
6
6
'
6
<
#
R e a zio n e
#
B
' 6
162
E"
,0
"
α
2
∆
.KVL
0
"
0
"
"
"
0
"
"
"
"
/
* +. + @
'
,$
#.+@
6
<
#
R e a zio n e
#
B
' <
E"
#
' #
163
1
• Il ciclo di Krebs è al centro del metabolismo.
• Le vie degradative (catabolismo) lo
alimentano, le vie sintetiche (anabolismo) ne
usano i componenti.
• È una via “ANFIBOLICA”, opera infatti sia nel
catabolismo che nell’anabolismo cellulare.
• Tutte le reazioni avvengono nella matrice
mitocondriale.
• Nei mitocondri vi sono anche gli enzimi della
fosforilazione ossidativa e quelli della
ossidazione degli acidi grassi e degli
aminoacidi.
#
' B
%
2#
3 #5+, # + +
%
+ (& ) &)
6
+ +5+ +,$
*
+ ()
%
&'
%
%
.A
%
%
$*.$
# + +
#**+
%
%
%
%
%
%
0
%
%
%
&'
&
%
%&
%
%
%
& %
# (
&
%
%
%&
%
%
,0
%
%
& %
%
, (&
%
%
%
, (
"
%
%
%
%
&
0
%
"
%
%
& %
&
0
*
%
"
%
%
%
&
%
+ +,$
%
0
α
%
%
0
"
%
%
+ ()
+ (& ) &)
%
%
%
%
&
%
+ (& ) &)
+ ()
&%
%
%
# + +
#**+
+* # +
+
5
@
%
%
2
( )
%
%
%
%
%
6 +,$
#
#5+, # + +
'
164
C
- "
"
• Gli intermedi del ciclo di Krebs sono risintetizzati
dalle reazioni anaplerotiche.
• La concentrazione degli intermedi nel ciclo rimane
pressoché costante.
• La principale reazione anaplerotica è quella che porta
alla produzione di ossalacetato da CO2 e piruvato. La
reazione è catalizzata dalla piruvato carbossilasi.
• La produzione di ossalacetato avviene
principalmente nel rene e nel fegato.
• La piruvato carbossilasi è fortemente stimolata da
acetil-CoA.
#
' M
• Ci sono prove che suggeriscono la
formazione di complessi multienzimatici
per il ciclo di Krebs.
• Ciò potrebbe facilitare la canalizzazione
dei substrati tra i siti attivi.
#
''
165
"
3 2
"
$ (
$ 2"
$ 2"
"
- "
- "
3 :
α
0
$ :
;
$ :;
3 :;
"
?
0 0
?
"
0
" 9
0
"
"
4
0
0"
"
- " 9
"
"
?
"
"
+ (& "
0 0
0
"
"
#
''
"
• L’inibizione della citrato sintasi da ATP
è eliminata da ADP.
• Nei muscoli di vertebrato lo ione Ca++
attiva la isocitrato deidrogenasi e la αchetoglutarato deidrogenasi.
• Le velocità della glicolisi e del ciclo di
Krebs sono integrate.
#
''
166
1
%
+ (& ) &)
+ ()
&'
%&
%
%
%
%
%
%
%
%&
%
&
,0
%
%
%
%
& %
%
&'
, (&
%
%
&
%
, (
%
%
%
0
%
%
&'
&
%
& %
%
%
%
%
%
%
&
%
%
%
%
%
%
"
%
&
0
%
"
%
%
& %
&
0
*
%
"
%
%
2
( )
%
0
α
%
%
&
%
%
0
"
%
%
+ ()
+ (& ) &)
%
%
%
%
&
%
+ (& ) &)
+
&%
%
%
()
%
%
%
%
%
%
%
#
''B
(
3 +
"
"
"
"
3
-0
D
0
"
3 2
"
"
9
4
(
"
" - "
"
"
--
3 2!
"
"
&4
" β
0
3 + &
0 "
#
"
"
''
169
(
3 +
-0
"
"
"
"
" - "
"
*
0
@
(
E % 2
3
D
"
"
"
3 2
!
9
4
(
"
"
--
3 2!
"
%
%
"
&4
" β
,0
2
0
=
"
0
"
%
0
"
&
3 + &
0 "
5
"
#
''M
3 2
0
"
.E )E )E'/
A "
" %
1
4
"
" 9
+ (&4 0"
(& 4 0" * .
- "
0
/
"
1
"
"
0
"
4
4
"
4
"
" 4
"
0
/
A
0
- "
-0
0
3 :;
,
3
.
3 :;
#
A
"
"
'6
170