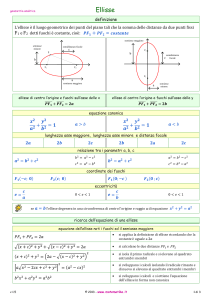
Scrivi l'equazione dell'ellisse, riferita al centro e agli assi, passante per i punti
(
( 165 )
A 3;
)
e
12
e determina le coordinate dei fuochi e l'eccentricità. Scrivi poi l'equazione della
5
parabola con la concavità rivolta verso l'alto ,passante per i fuochi dell'ellisse e avente vertice nel
punto di intersezione dell'ellisse con l'asse y.
B −4 ;
L'equazione dell'ellisse è
2
2
x y
+ =1
a2 b2
imponendo il passaggio per due punti
{
256
(
25 )
9
+
=1
a
2
2
b
da cui
144
25
16
+
=1
2
a
b2
( )
{
9 256
+
=1
a 2 25 b2
16 144
+
=1
a 2 25 b2
da cui
{
225 b 2+256 a 2=25 a 2 b2
400 b2+144 a 2=25 a 2 b2
per il confronto delle due equazioni, il sistema è equivalente a
{
2
2
2
225 b +256 a =400 b +144 a
2
2
2 2
400 b +144 a =25 a b
2
da cui
{
{
112 a 2=175 b2
ovvero
400 b2+144 a 2=25 a 2 b2
16 a 2=25 b 2
da cui
400 b +144 a 2=25 a 2 b2
2
e
da cui
{
{
16 a 4=25 a 2 b2
2
2
4
400 b +144 a =16 a
256 a 2=400 b 2
256 a 2+144 a 2=16 a 4
{
2
da cui
e quindi
{
b =16
. L'equazione dell'ellisse è
a 2 =25
{
256 a 2=400 b 2
2
2
4
256 a +144 a =16 a
256 a 2=400 b 2
da cui
400 a 2=16 a 4
{
da cui
16 a 2=25 b2
e quindi
a 2=25
x2 y2
+ =1
25 16
si ha che c 2=25−16=9 e quindi le coordinate dei fuochi sono
c 3
cui l'eccentricità è e= = .
a 5
F 1(−3 ; 0) e
F 2 (3 ; 0) , da
L'ellisse interseca l'asse y nei punti di coordinate (0;4) e (0;-4) , e quindi la parabola avrà concavità
verso l'alto solo se ha il vertice nel punto (0;-4). Inoltre, essa passa per (-3;0) e (3;0). Di
conseguenza, avrà equazione
y=a x 2−4
imponendo il passaggio per i due fuochi
4 2
y= x −4
9