testo e soluzione

FISICA per SCIENZE BIOLOGICHE, A.A. 2012/2013
Prova scritta del 18 Luglio 2013
SCRIVERE IN MODO CHIARO. DESCRIVERE I PROCEDIMENTI E LE FORMULE USATE.
SOSTITUIRE I VALORI NUMERICI SOLO ALLA FINE. INDICARE LE UNITA` DI MISURA.
MECCANICA: Un corpo di massa m = 0.4 kg poggia su un
gradino orizzontale di altezza H = 1 m e comprime di un tratto
d = 10 cm una molla di costante elastica k = 103 N/m, come
mostrato in figura. Determinare:
a) la velocità con cui il corpo si stacca dalla molla dopo che questa è ritornata alla
lunghezza naturale, e la velocità raggiunta alla fine del tratto orizzontale OA = 2m,
supponendo che lungo il percorso OA la superficie sia scabra e mostri un coefficiente di
attrito pari a µ = 0.2;
b) la distanza massima orizzontale raggiunta, dopo la caduta dal gradino.
TERMODINAMICA: una mole di gas perfetto monoatomico compie le seguenti
trasformazioni termodinamiche: AB: trasformazione isocora dalla pressione pA = 3 atm
alla pressione pB = 2 atm, con VA = 1 l; BC: espansione isoterma fino al volume VC = 2
l; CD: espansione isobara fino al volume VD = 3l.
a) Disegnare le trasformazioni nel piano p-V e calcolare le coordinate termodinamiche
(p,V,T) nei punti A, B, C e D;
b) Calcolare la variazione di energia interna, il calore scambiato ed il lavoro fatto dal gas
nelle tre trasformazioni. [N.B. R= 8.31 J/Kmole =0.082 l atmo /Kmole ]
FLUIDI: Un cubo di lato L = 10 cm, di materiale con densità
rC = 0.5 × 103 kg/m3, è mantenuto completamente immerso
in acqua, a profondità H = 1m, mediante una fune (vedi figura).
Determinare:
a) La tensione T della fune;
b) La velocità con cui il corpo arriva in superficie, dopo che la
fune è stata tagliata.
ELETTROSTATICA: Una lamina piana infinita è carica uniformemente con densità di
carica s =+10-9 C/m2. La lamina è posta nell’origine degli assi cartesiani (x,y),
perpendicolarmente all’asse x. Nel punto A di coordinate (2d,0), con d = 1m, è posta
una carica sorgente Q = +10-9 C. Si calcoli :
a) Modulo, direzione e verso del campo elettrico totale, nel punto B di coordinate (d,0);
b) Il lavoro compiuto dalla forza elettrica dovuta alla lamina, dalla forza elettrica
dovuta alla carica Q e dalla forza elettrica totale per portare una carica di prova q0 =
10-12 C dal punto B al punto C di coordinate (d,d); [N.B. ε o= 8.85 10-12 C2/ N m2
oppure k= 8.99 109 N m2/ C2 ]
Soluzione Esercizio MECCANICA
a) Per il principio di conservazione dell’energia meccanica, quando la molla torna a riposo
l’energia potenziale elastica della molla viene convertita completamente in energia cinetica
del corpo:
da cui segue che
Per il teorema
lavoro-energia cinetica, il lavoro compiuto della forza di attrito lungo il tratto OA è pari alla
variazione di energia cinetica del corpo:
  1
1
Fatt ⋅ L = mv 2f − mv i2
2
2
1 2 1 2
−µmgL = mv f − mv i
2
2
v f = v i2 − 2 µgL = 4.14m /s
b) Il corpo cadendo dal gradino compie un moto parabolico, soggetto alla sola accelerazione
€
di gravità. L’ equazione del moto lungo y è quindi:
tempo di caduta è quindi:
il
Essendo il moto lungo x rettilineo
ed uniforme, la massima distanza x raggiunta è pari a
Soluzione Esercizio TERMODINAMICA
a) Le coordinate termodinamiche valgono:
Stato A:
Stato B:
Stato C:
Stato D:
b) La variazione di energia interna DE, il lavoro W ed il calore scambiato si ottengono dal 1.
Principio della termodinamica:
trasformazione AB:
trasformazione BC:
trasformazione CD:
Soluzione Esercizio FLUIDI
a) Il cubo è soggetto alla Spinta di Archimede, alla forza Peso e alla Tensione della fune ed
è in condizione di equilibrio. Pertanto , tenendo conto del verso delle forze agenti , si ha : SA
– P– T = 0 dove SA , P, e T sono i moduli rispettivamente della Spinta di Archimede, della
forza Peso e della Tensione della fune . Si ricava T: T = SA – P = V g (ρH2O – ρC ) dove V
è il volume del cubo ,
ρH2O e ρC sono rispettivamente la densità dell’acqua e del cubo.
Sostituendo i valori numerici ( V = 10 -3 m 3 , ρH2O = 10 3 kg / m 3 ) si ottiene T = 4.9
N
b) Quando la fune viene tagliata il cubo è soggetto ad una forza risultante F di modulo
uguale a quello della Tensione, diretta lungo la verticale, verso l’alto Quando il cubo
raggiunge la superficie dell’acqua , senza emergere, ha percorso nell’acqua un tratto D =
0.95 m. Per il teorema Lavoro - Variazione Energia Cinetica , il Lavoro compiuto dalla Forza
risultante uguaglia la variazione dell’energia cinetica in questo tratto e pertanto : L = F D =
½ m v2 dove v è la velocità finale ( quella iniziale è nulla ) . Si ricava v : v = (2FD/m) ½ e
sostituendo i valori numerici si trova v = 4.3 m/s
Soluzione Esercizio ELETTROSTATICA
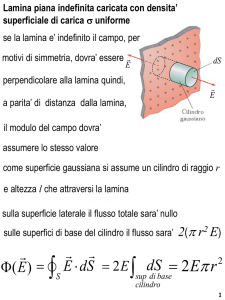
a) Il campo elettrostatico creato dalla lamina nel punto ( d, 0), EL , è perpendicolare alla
lamina, con verso uscente dalla lamina e ha modulo EL = σ / 2 ε o , quindi : EL = σ / 2 ε o
( i ) dove i è il versore dell’asse x. Il campo elettrostatico creato dalla carica Q nel punto
B=(d,0), EQ , è diretto lungo la congiungente Q e il punto B, verso uscente da Q , e ha
modulo EQ = k Q / d 2 , quindi : EQ = - k Q / d 2 ( i ). Il Campo Elettrostatico totale nel
punto B=(d,0) è la somma vettoriale di EL e di E. Sostituendo i valori numerici si trova: EL
= 56.5 (N/C) i , EQ = - 9 (N/C) i. Il campo totale ETOT = 47.5 (N/C) i
b) Il lavoro compiuto dalla forza elettrostatica creata dalla lamina, FL è nullo , in quanto la
forza e lo spostamento sono perpendicolari. Il lavoro L Q compiuto dalla forza elettrostatica
FQ dovuta alla carica Q, si calcola facilmente come : L Q = U(B) –U(C) dove U(B) e U(C),
valori dell’energia potenziale associata al campo creato dalla carica Q nei punti B e C, sono :
U(B) = k Q q / d e U(C)= kQq / d √ 2 Sostituendo i valori numerici si trova: L Q = 2.6
10 – 12 J Il lavoro totale L TOT = L Q = 2.6 10 – 12 J