FISICA per SCIENZE BIOLOGICHE A.A. 2012/2013
II Compitino– 21 Giugno 2013
FLUIDI: Un cubo di lato L=0.15 m ha una cavità vuota al proprio interno, pari ad 1/5 del suo volume e la
densità del materiale di cui è costituito è pari alla metà di quella dell’acqua. Il cubo, completamente immerso in
una vasca piena d’acqua, è trattenuto con una fune, ancorata al fondo della vasca.
a) Calcolare la spinta di Archimede e la tensione della fune, specificando modulo, direzione e verso;
b) Supposto di tagliare la fune, calcolare il volume di corpo immerso in acqua dopo che il corpo ha raggiunto
una condizione di equilibrio di galleggiamento.
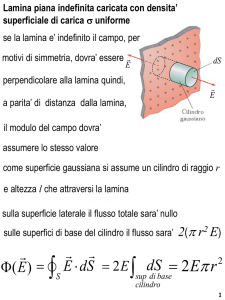
ELETTROSTATICA Una lamina piana, infinitamente estesa ,
uniformemente carica con densità superficiale σ = + 4 10 -9 C/m2 , è
posta nel piano (x,y) , passante per l’origine O di un sistema d’assi
(x,y,z). Nel punto A del semiasse positivo z, è fissata una carica Q = +
2 10 -9 C, a distanza OA= 4m dalla lamina . Si determinino :
a) gli eventuali punti dell’asse z in cui il campo elettrostatico totale è
nullo.
b) il lavoro totale compiuto dalle forze elettrostatiche per spostare la
carica q , q = + 2 10 - 12 C, dal punto B al punto C lungo il semiasse
positivo z, sapendo che OB ed OC sono rspettivamente 6 m e 8 m .
[Note: ε0 = 8.85 10-12 C2/Nm2 ]
z
C
B
+QA
O
x
y
+σ
TERMODINAMICA Due moli di un gas perfetto biatomico compiono il ciclo A→ B→ C→ A costituito dalle
seguenti trasformazioni reversibili: A→ B isobara con VB = 2VA , B→ C isocora con pC = (1/4) pB , C→ A
trasformazione in cui la pressione aumenta linearmente fino a pA , mentre il volume decresce da VC fino a VA .
Inoltre pA= 4 atmosfere e VA = 2 litri.
a) Si rappresentino le tre trasformazioni in un diagramma ( V, p) e si calcolino le temperature di A, B e C; la
quantità di calore totale scambiata e il lavoro compiuto dal gas nell’intero ciclo.
b) Si calcoli la variazione di energia interna del gas per le trasformazioni A→ B→ C e per le trasformazioni
A→ B’→ C , dove A→ B’ è isoterma e B’C isocora.
c) Facoltativo: Si calcoli il rendimento per il ciclo A→ B→ C→ A
Nota: 8.31 J/Kmole =0.082 l atm /K mol)
-----------------------------------------------------------------------------------------------------------------------------------------Recupero Cinematica:
Determinare il tempo impiegato per raggiungere il suolo da un corpo lanciato orizzontalmente da una quota h =
20 cm, con velocità in modulo pari a V = 0.79 m/s.
Recupero Dinamica:
Un corpo di massa M = 300 g percorre un tratto orizzontale scabro con coefficiente di attrito dinamico µ = 0.75.
Calcolare la forza Fapp che si deve applicare, modulo direzione e verso, affinchè la velocità del corpo sia
costante.
Recupero Lavoro-Energia:
Un corpo di massa M = 300 g viene lanciato verso il basso, con velocità in modulo vA = 1 m/s, lungo un piano
inclinato di un angolo θ = 60°, partendo da un un punto A a quota H = 2.5 m rispetto alla base del piano. Giunto
in B, alla base del piano, procede su un tratto orizzontale liscio, fino al punto C, dove urta in modo
completamente anelastico contro un corpo di massa 3M.
Determinare la velocità del corpo nel punto B (alla base del piano inclinato), nel punto C (alla fine del tratto
orizzontale liscio) e la velocità dei due corpi immediatamente dopo l’urto anelastico.
SCRIVERE IN MODO CHIARO. GIUSTIFICARE I PROCEDIMENTI. SOSTITUIRE I VALORI
NUMERICI SOLO ALLA FINE. NON SCORDARE LE UNITA` DI MISURA. Testi, soluzioni ed esiti alle pagine:
www2.fisica.unimi.it/bettega, www.mi.infn.it/~sleoni
SOLUZIONE ESERCIZIO FLUIDI
a) La spinta di Archimede è pari al peso di fluido spostato ed è diretta verso lpalto, in verso opposto alla forza
peso del cocrpo e alla tensione della fune. Essendo il corpo completamente immerso in acqua si ottiene:
FA = mfg = rfVg = rfL3g
= 103 (0.15)3 9.8 N = 33.1 N
La tensione della fune si ottiene dal bilancio delle forze:
a) Tagliata la fune, il corpo risale in superficie. Il volume di corpo immerso di ottiene dal bilancio fra la forza
peso del corpo e la spinta di Archimede:
SOLUZIONE ESERCIZIO ELETTROSTATICA
a)Il campo elettrostatico creato dalla lamina è in ogni punto perpendicolare alla lamina , uscente dalla lamina
ed ha modulo /E lamina / = σ / 2ε0 . Indicato con k il versore dell’asse z, il campo elettrostatico creato
dalla lamina è E lamina = (σ / 2ε0 ) (k) ( per z>0 ) ed E lamina = (σ / 2ε0 ) (-k ) ( per z<0 ) .
Nei punti dell’asse z il campo creato dalla carica Q è parallelo all’asse z , uscente dalla carica Q, ed ha
modulo /EQ / = KQ/ (z-4)2 . E’ pertanto EQ = KQ/ (z-4)2 ( k) ( per z>4 ) ed EQ = KQ/ (z-4)2 (- k)
per ( per z<4 ) , dove K = 1/ 4 π ε0 .
I punti dell’asse z in cui il campo elettrostatico totale può essere nullo sono quelli compresi tra O ed A ( 0<
z <4) in quanto solo in questo tratto il campo creato dalla lamina e quello creato dalla carica Q sono paralleli
ed hanno verso opposto. Per z>4 e z<0 i due campi sono invece paralleli ed equiversi.
Il campo totale sarà nullo nel punto P , a quota z (con 0<z<4), in cui i moduli dei due campi sono uguali .
Si ha quindi : (σ / 2ε0 ) = KQ/ (z-4)2. Sostituiti i valori numerici e risolta l’equazione di secondo grado in z ,
si ottengono due soluzioni delle quali solo una è accettabile in quanto minore di 4, ed è z= 3.72m.
b) Il lavoro compiuto dalle forze elettrostatiche esercitate dalla lamina e dalla carica Q mentre q si sposta da
B a C sono rispettivamente:
Llamina = q (σ / 2ε0 ) ( BC) = 0,904 10 -9 J
L Q = U (B) –U (C) = Kq Q ( 1/ AB -1/ AC) = 0,009 10 -9 J
Il lavoro totale è quindi L = 0,913 10 -9 J
SOLUZIONE ESERCIZIO TERMODINAMICA
a)
p
A
B
C
V
TA = pA VA /nR = 48.78 K
TB = pB VB /nR = pA 2VA /nR = 2 TA = 97.56 K
TC = pC VC /nR = (1/4) pA 2VA /nR = (1/2) TA = 24.39 K
Il Lavoro compiuto dal gas nell’intero ciclo è L = L AB + L BC + L CA , ed è uguale all’area del triangolo ABC.
LCICLO = (VB - VA) (pB - pC ) / 2 = ( 3/8) pA VA = 303 J
QCICLO = LCICLO = 303 J
b) ΔE ABC : poichè E è una funzione di stato ΔE ABC = ΔE AC = n cV (TC - TA ) = -1010 J
Inoltre ΔE AB’ C = ΔE ABC = -1010 J
c) Facoltativo
Il rendimento ρ = LCICLO / Qassorbito CICLO .
Le quantità di calore scambiate dal gas nelle trasformazioni del ciclo sono :
QAB = n cp (TB - TA ) = n ( 7/2) R TA = ( 7/2) pA VA = 2828 J , positiva quindi assorbita
QBC = n cV (TC - TB ) = n ( 5/2) R ( -3/2)TA = ( - 15/4) pA VA = -3030 J , ceduta
QCA = QCICLO - QAB - QBC = 505 J assorbita
Qassorbito CICLO = 3333J
e ρ = LCICLO / Qassorbito CICLO = 303/ 3333 = 0,09
(cV = (5/2) R )
SOLUZIONE RECUPERO CINEMATICA
Il tempo impiegato per raggiungere il suolo si ottiene dalla legge oraria lungo y (moto uniformemente
accelerato) :
La distanza orizzontale percorsa è pari a:
x = Vt = 0.79 m/s x 0.2 s = 0.158 m
SOLUZIONE RECUPERO DINAMICA
Affinchè la velocità sia costante la risultante delle forze deve essere nulla:
La forza da applicare ha stessa direzione ma verso opposto della forza di attrito che si oppone al moto.
SOLUZIONE RECUPERO LAVORO-ENERGIA
La velocità in B si ottiene applicando la conservazione dell’energia meccanica:
La velocità in C è a stessa in B, non essendoci attrito ed essendo il piano orizzontale.
La velocità V dei due corpi dopo l’urto anelastico si ottiene applicando la conservazione della quantità di moto: