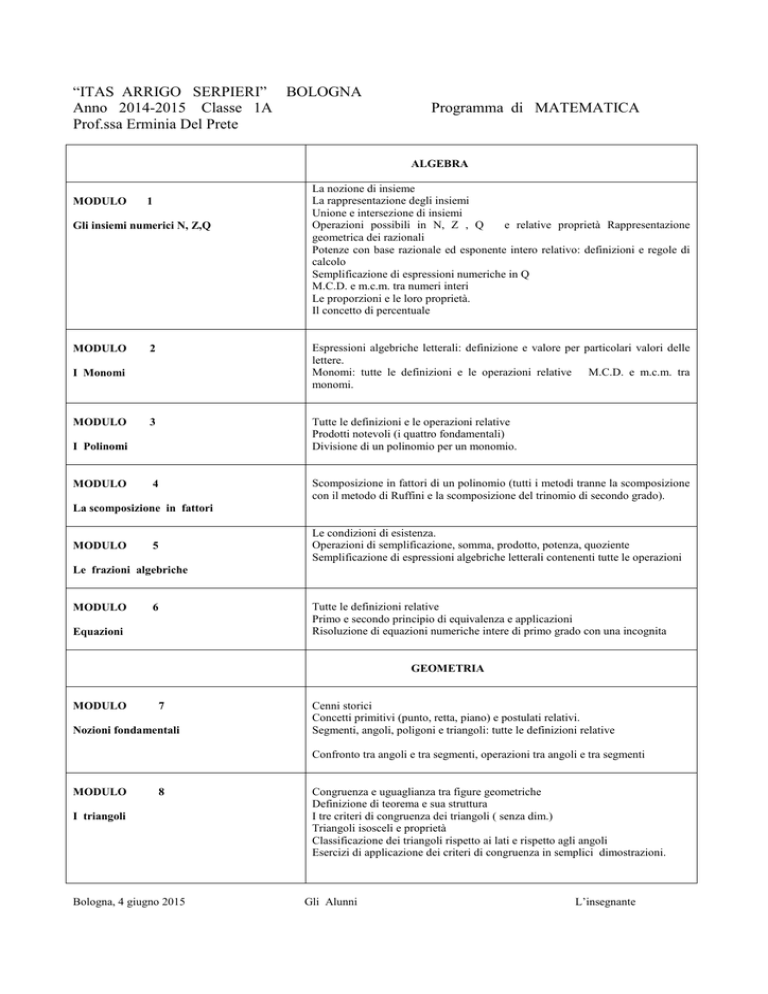
“ITAS ARRIGO SERPIERI” BOLOGNA
Anno 2014-2015 Classe 1A
Prof.ssa Erminia Del Prete
Programma di MATEMATICA
ALGEBRA
MODULO
1
Gli insiemi numerici N, Z,Q
MODULO
2
Espressioni algebriche letterali: definizione e valore per particolari valori delle
lettere.
Monomi: tutte le definizioni e le operazioni relative M.C.D. e m.c.m. tra
monomi.
3
Tutte le definizioni e le operazioni relative
Prodotti notevoli (i quattro fondamentali)
Divisione di un polinomio per un monomio.
4
Scomposizione in fattori di un polinomio (tutti i metodi tranne la scomposizione
con il metodo di Ruffini e la scomposizione del trinomio di secondo grado).
I Monomi
MODULO
I Polinomi
MODULO
La nozione di insieme
La rappresentazione degli insiemi
Unione e intersezione di insiemi
Operazioni possibili in N, Z , Q
e relative proprietà Rappresentazione
geometrica dei razionali
Potenze con base razionale ed esponente intero relativo: definizioni e regole di
calcolo
Semplificazione di espressioni numeriche in Q
M.C.D. e m.c.m. tra numeri interi
Le proporzioni e le loro proprietà.
Il concetto di percentuale
La scomposizione in fattori
MODULO
Le condizioni di esistenza.
Operazioni di semplificazione, somma, prodotto, potenza, quoziente
Semplificazione di espressioni algebriche letterali contenenti tutte le operazioni
5
Le frazioni algebriche
MODULO
Tutte le definizioni relative
Primo e secondo principio di equivalenza e applicazioni
Risoluzione di equazioni numeriche intere di primo grado con una incognita
6
Equazioni
GEOMETRIA
MODULO
7
Nozioni fondamentali
Cenni storici
Concetti primitivi (punto, retta, piano) e postulati relativi.
Segmenti, angoli, poligoni e triangoli: tutte le definizioni relative
Confronto tra angoli e tra segmenti, operazioni tra angoli e tra segmenti
MODULO
8
I triangoli
Bologna, 4 giugno 2015
Congruenza e uguaglianza tra figure geometriche
Definizione di teorema e sua struttura
I tre criteri di congruenza dei triangoli ( senza dim.)
Triangoli isosceli e proprietà
Classificazione dei triangoli rispetto ai lati e rispetto agli angoli
Esercizi di applicazione dei criteri di congruenza in semplici dimostrazioni.
Gli Alunni
L’insegnante












