Quattro triangoli equiestesi
Problema
Sia ABC un triangolo qualsiasi. Costruire sui lati del triangolo, esternamente al triangolo, i quadrati aventi
per lati i lati del triangolo, quindi unire i vertici dei tre quadrati individuando l’esagono convesso
contenente il triangolo ABC e i tre quadrati. L’esagono è composto dall’unione del triangolo ABC, dai tre
quadrati e da altri tre triangoli T1, T2, T3, ciascuno dei quali ha uno dei suoi vertici coincidente con un
vertice di ABC. Dimostrare che i triangoli T1, T2, T3, sono equiestesi al triangolo ABC.
Soluzione
Prima dimostrazione (applicazione della trigonometria)
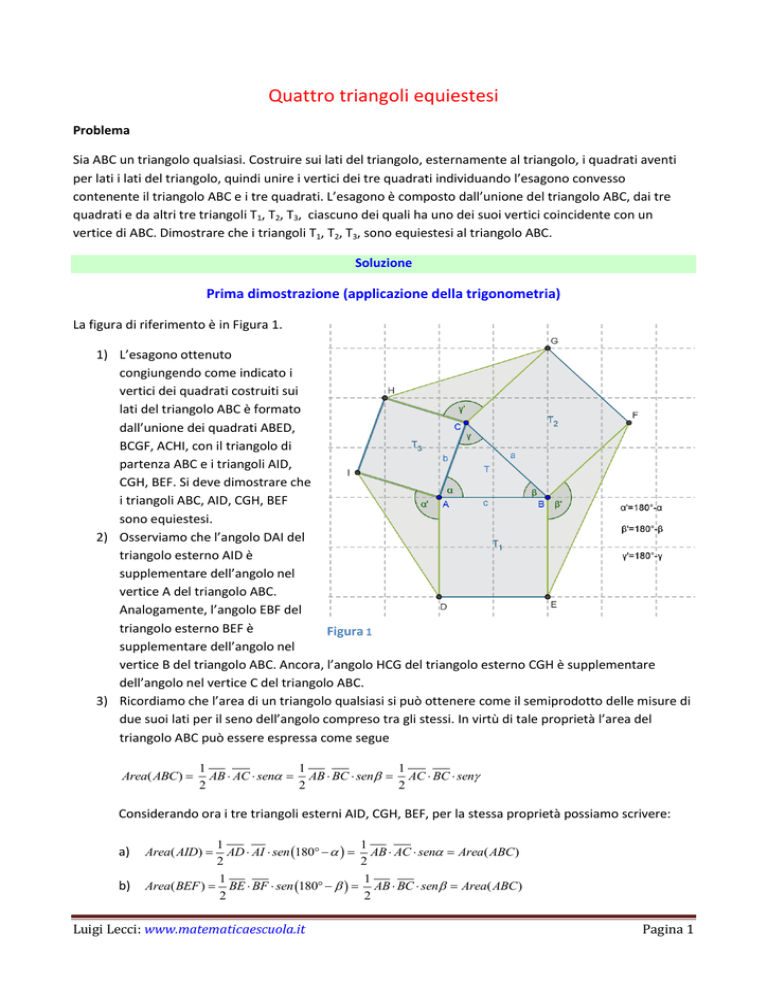
La figura di riferimento è in Figura 1.
1) L’esagono ottenuto
congiungendo come indicato i
vertici dei quadrati costruiti sui
lati del triangolo ABC è formato
dall’unione dei quadrati ABED,
BCGF, ACHI, con il triangolo di
partenza ABC e i triangoli AID,
CGH, BEF. Si deve dimostrare che
i triangoli ABC, AID, CGH, BEF
sono equiestesi.
2) Osserviamo che l’angolo DAI del
triangolo esterno AID è
supplementare dell’angolo nel
vertice A del triangolo ABC.
Analogamente, l’angolo EBF del
triangolo esterno BEF è
Figura 1
supplementare dell’angolo nel
vertice B del triangolo ABC. Ancora, l’angolo HCG del triangolo esterno CGH è supplementare
dell’angolo nel vertice C del triangolo ABC.
3) Ricordiamo che l’area di un triangolo qualsiasi si può ottenere come il semiprodotto delle misure di
due suoi lati per il seno dell’angolo compreso tra gli stessi. In virtù di tale proprietà l’area del
triangolo ABC può essere espressa come segue
Area( ABC )
1
1
1
AB AC sen AB BC sen AC BC sen
2
2
2
Considerando ora i tre triangoli esterni AID, CGH, BEF, per la stessa proprietà possiamo scrivere:
a)
b)
1
1
AD AI sen 180 AB AC sen Area( ABC )
2
2
1
1
Area( BEF ) BE BF sen 180 AB BC sen Area( ABC )
2
2
Area( AID)
Luigi Lecci: www.matematicaescuola.it
Pagina 1
c)
1
1
Area(CGH ) CG CH sen 180 BC AC sen Area( ABC )
2
2
I triangoli AID, BEF, CGH, hanno tutti la stessa area del triangolo ABC, quindi sono equiestesi a
quest’ultimo; in definitiva i quattro triangoli ABC, AID, BEF, CGH, sono equiestesi. C.V.D.
Di seguito riportiamo le figure corrispondenti nel caso che ABC sia un triangolo rettangolo isoscele,
con angolo retto nel vertice C (Figura 2) e nel caso che ABC sia un triangolo rettangolo qualsiasi con
angolo retto nel vertice A (Figura 3).
Figura 2
Il triangolo ABC è rettangolo
isoscele con l’angolo retto nel
vertice C.
Figura 3
Il triangolo ABC è rettangolo con
l’angolo retto nel vertice A.
Luigi Lecci: www.matematicaescuola.it
Pagina 2
Seconda dimostrazione (applicazione di una proprietà dei triangoli sull’equiestensione)
Facciamo riferimento alla Figura 4.
***
Premessa
Ricordiamo la seguente proprietà
dei triangoli:
1) “ un triangolo qualsiasi è
equiesteso ad un
parallelogramma avente per
base un lato del triangolo e
per altezza metà dell’altezza
del triangolo relativa al lato
considerato”.
Come applicazione della
proprietà 1) discende la seguente
proprietà per due triangoli
qualsiasi:
Figura 4
2) “se due triangoli hanno congruenti un lato e le altezze relative al suddetto lato allora sono
equiestesi”.
Infatti, si possono trasformare i due triangoli nel parallelogramma equiesteso avente come base il
lato congruente dei due triangoli considerati e come altezza metà del segmento altezza dei due
triangoli relativa al suddetto lato congruente.
***
Vogliamo provare che i triangoli ABC, ADI sono equiestesi
a) Consideriamo per i vertici A e C rispettivamente le rette q ed s perpendicolari alla retta t del lato
AB; sia K l’intersezione di s con t. Tracciamo ancora dal vertice I del quadrato ACHI la retta r
perpendicolare alla retta q e sia J il punto di intersezione tra le due rette.
b) Confrontiamo i triangoli AJI, AKI, rettangoli rispettivamente in J e K.
Osserviamo che i due triangoli hanno congruenti le ipotenuse AI, AC, perché lati dello stesso
quadrato; inoltre, gli angoli acuti IAJ, CAK sono complementari dello stesso angolo acuto JAC, perciò
sono tra loro congruenti; ciò basta per affermare che i due triangoli AJI, AKC sono congruenti e
quindi avranno i lati omologhi IJ, CK congruenti.
c) I due triangoli ABC, ADI, hanno congruenti i lati AC e AD e le altezze relative CK, IJ e quindi per la
proprietà 2) riportata nella premessa i due triangoli sono equiestesi.
C.V.D.
Luigi Lecci: www.matematicaescuola.it
Pagina 3
Osservazione sulla Figura 4
Nella Figura 4 il triangolo ABC è acutangolo; se però il triangolo è rettangolo o ottusangolo la
dimostrazione dell’equiestensione dei due triangoli ABC, ADC ha percorsi diversi.
Caso in cui ABC sia rettangolo in A (Figura 5)
Caso in cui il triangolo ABC sia ottusangolo in A (Figura 6).
Figura 5
Il triangolo ABC è rettangolo con
l’angolo retto nel vertice A.
In questo caso coincidono le
rette q ed s, e le rette r e t,
nonché i punti J e K con A. I
triangoli ABC, ADI sono rettangoli
e congruenti, e a maggior ragione
sono equiestesi. Per dimostrare
che ABC è equiesteso a ciascuno
dei triangoli BEF, CGH si
predispone la figura così come
fatto nella Figura 4 per la
dimostrazione
dell’equiestensione dei triangoli
ABC, ADI.
Figura 6
Il triangolo ABC è ottusangolo
con l’angolo ottuso nel vertice A.
L’altezza CK relativa ad AB è
esterna al triangolo. Si
confrontano i triangoli rettangoli
ACK, AIJ e si prova che sono
congruenti perché hanno
congruenti le ipotenuse AC, AI e
gli angoli acuti CAK, IAJ perché
complementari dello stesso
angolo IAK. Come conseguenza si
conclude che CKIJ.
A questo punto si può affermare
che sono equiestesi i triangoli
ABC, ADI per avere congruenti i
lati AB, AD e le altezze relative.
Luigi Lecci: www.matematicaescuola.it
Pagina 4
Equiestensione dei triangoli ABC, BEF e CGH
Si consegue la tesi seguendo procedimenti analoghi a quello descritto per la dimostrazione
dell’equiestensione dei triangoli ABC, ADI, predisponendo le apposite figure di riferimento.
La dimostrazione dell’equiestensione dei triangoli ABC, AID, BEF, CGH, è acquisita.
Luigi Lecci: www.matematicaescuola.it
Pagina 5












