www.matematicamente.it
Nicola De Rosa
maturità 2015
Esame di stato di istruzione secondaria superiore
Indirizzi: Scientifico Comunicazione Opzione Sportiva
Tema di matematica
Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario
PROBLEMA 1
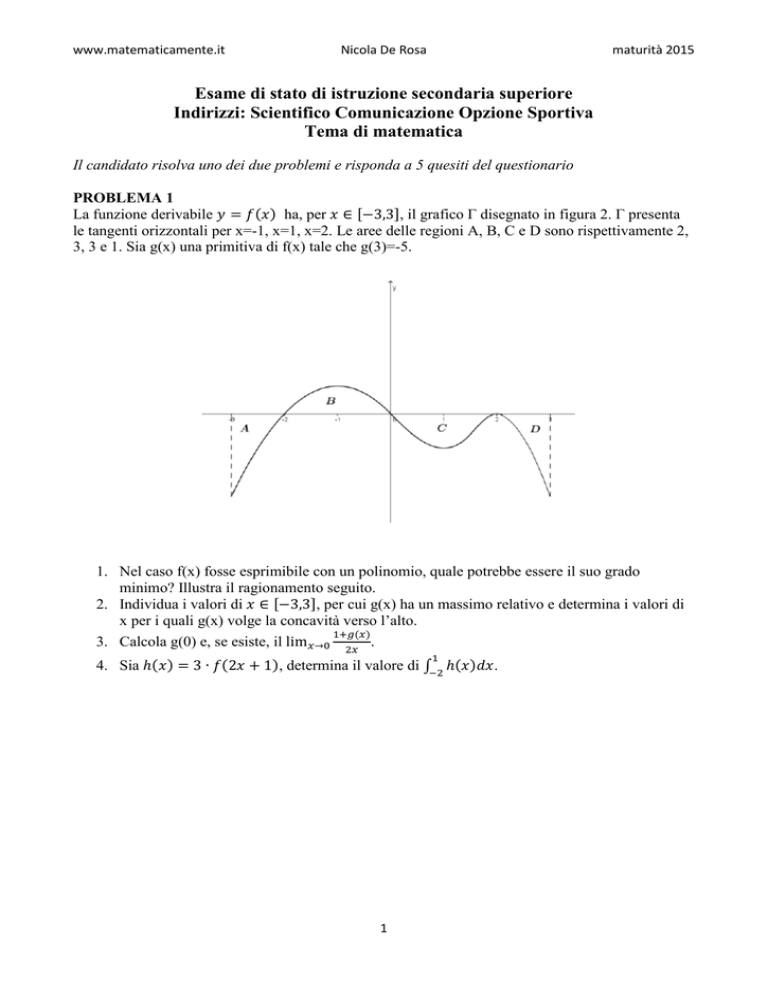
La funzione derivabile
ha, per
, il grafico Γ disegnato in figura 2. Γ presenta
le tangenti orizzontali per x=-1, x=1, x=2. Le aree delle regioni A, B, C e D sono rispettivamente 2,
3, 3 e 1. Sia g(x) una primitiva di f(x) tale che g(3)=-5.
1. Nel caso f(x) fosse esprimibile con un polinomio, quale potrebbe essere il suo grado
minimo? Illustra il ragionamento seguito.
2. Individua i valori di
, per cui g(x) ha un massimo relativo e determina i valori di
x per i quali g(x) volge la concavità verso l’alto.
3. Calcola g(0) e, se esiste, il
.
4. Sia
, determina il valore di
1
.
www.matematicamente.it
Nicola De Rosa
maturità 2015
SVOLGIMENTO a cura di Nicola De Rosa
1. Il grado di f (x) nell’ipotesi che sia una funzione polinomiale è almeno quarto. Infatti ha tre
punti a tangente orizzontale, dunque la sua derivata deve annullarsi in tre punti e quindi è un
polinomio di grado non inferiore al terzo. A conferma, una retta opportunamente scelta interseca il
grafico della curva in quattro punti.
2. La primitiva g (x) ha monotonia stabilita dal segno di f (x) secondo il seguente schema:
-3
-2
-1
0
1
2
3
segno di f (x)
monotonia di g (x)
quindi g (x) ha un massimo relativo in x 0 (gli altri due zeri di corrispondono ad un minimo in
x 2 ed un flesso a tangente orizzontale in x 2 ).
Il verso della concavità di g (x) è fissato dal segno di g ( x) f ( x) ; in particolare, la concavità è
verso l’alto dove f (x) è positiva, quindi dove f (x) è crescente. Dal grafico si desume che ciò
avviene negli intervalli 3,1 e 1,2 .
x
3. Detta g 0 ( x) la primitiva di f (x) che si annulla per x 3 , ovvero: g 0 ( x) f (t )dt , la
3
funzione richiesta g (x) è data da: g ( x) g 0 ( x) K , con K opportuna costante.
Dai dati forniti sulle aree delle regioni e dal segno degli integrali definiti corrispondenti si trova:
g 0 (3) 2 3 3 1 3 , per cui dalla richiesta che sia: g (3) 5 si ottiene:
x
5 3 K K 2 , quindi è: g ( x) f (t )dt 2 .
3
0
Di conseguenza: g (0) f (t )dt 2 3 2 1 ;
3
il limite richiesto si calcola con la regola di De L’Hopital:
1 g ( x) ( H )
g ( x)
f ( x)
lim
lim
0,
x0
x0
x0
2x
2
2
lim
dove si è sfruttato il fatto che g ( x) f ( x) e che dal grafico di risulta f (0) 0 .
4. Si ha:
1
2
1
1
2
h( x)dx
h( x)dx 3 f (2 x 1)dx ; con la sostituzione:
2
3 3
3
9
f ( z )dz (2 3 3 1) .
3
2
2
2
2
1
z 2 x 1 dx dz
2
si ha:
www.matematicamente.it
Nicola De Rosa
maturità 2015
PROBLEMA 2
Assegnate le funzioni reali f x ln x e g x e x 2 , e indicati con F e G i loro grafici in un
riferimento cartesiano Oxy:
1. Stabilisci dominio e codominio delle funzioni f e g, e traccia quindi i grafici delle funzioni
ax f g x e bx g f x ;
2. determina l’equazione della retta , tangente a F nel suo punto di ascissa e 2 . Stabilisci inoltre se
esiste una retta s, parallela a r, che sia tangente a G;
3. determina l’equazione della retta , parallela alla bisettrice del primo quadrante, che sia tangente
a F. Dimostra che risulta essere tangente anche a G;
4. detta A la regione piana finita delimitata dall’asse , dalla retta di equazione
=
− 1 e dal
grafico G, calcola l’area di A e il volume del solido generato ruotando A intorno all’asse .
3
www.matematicamente.it
Nicola De Rosa
SVOLGIMENTO
La funzione f x ln x da dominio D f 0, e codominio C f R .
La funzione g x e x 2 da dominio Dg R e codominio C g 0, .
Di seguito i grafici nello stesso riferimento cartesiano:
Punto 1
Si ha
ax f g x ln e x2 x 2
bx g f x e ln x 2 e ln x e 2 x e 2 con x 0
4
maturità 2015
www.matematicamente.it
Punto 2
La
retta
Nicola De Rosa
tangente
f x ln x
a
maturità 2015
in
e ,2
2
ha
equazione
r : y f ' e 2 x e 2 2 e 2 x e 2 2 x e 2 1 .
La retta s parallela ad r ha equazione s : y e 2 x q . Per essere tangente a G deve essere
2
x 2
2
x 2 2
x 0
g ' x e
e e
ovvero e x2 e 2 x 0
x 2
x 2
2
2
2
2
g x e x q
e e x q e e x q q e
pertanto s : y e 2 x e 2 e il punto di tangenza è 0, e 2 .
Punto 3
La retta parallela alla bisettrice del primo e terzo quadrante ha equazione t : y x q . Essa è
tangente ad f x ln x se f ' x
1
1 x 1 pertanto il punto di tangenza è B= 1,0 e la retta
x
è t : y x 1.
La
retta
t : y x 1
è
tangente
anche
a
g x e x 2
x 2
x 2 0
g ' x 1
x 2
e 1
x 2
x2
pertanto il punto di tangenza è A=(2,1).
g x x 1
e x 1 e x 1 1 1
5
se
www.matematicamente.it
Nicola De Rosa
Punto 4
La regione A è di seguito raffigurata.
L’area della regione A è pari a:
e
2
0
x 2
x 12 1 1 e 2 1 1 e 2
x 1 dx e x 2
2 0 2
2
2
6
maturità 2015
www.matematicamente.it
Nicola De Rosa
maturità 2015
Il volume del solido dato dalla rotazione di A attorno all’asse delle ordinate è dato dal volume del
cono con raggio di base 2 ed altezza 2 cui va sottratta il volume del solido generato dalla rotazione
di g x e x 2 attorno all’asse delle ordinate.
Il volume del cono con raggio di base 2 ed altezza 2 è pari a
8
.
3
Invertendo la funzione g x e x 2 , si ha x ln y 2 nell’intervallo e 2 ,1 ; il volume del solido
generato dalla rotazione di g x e x 2 attorno all’asse delle ordinate è pari a
2
1
2
2
ln y 2 dy ln y 4 ln y 4dy ln y dy 4 ln y dy 4 ye
e
1
1
1
1
2
2
2
2
y ln
e
4 y ln y 4 y
y 2 y ln y 2 y 2 4e 4e
y ln y 2 y ln y 2 y
2
2
1
e
1
e2
e2
1
2
e 2
2
e
4 y
8
2
2 1 e 2 2e 2
3
3
7
2e 2 2 1 e 2
Il volume finale è
1
e2
2
www.matematicamente.it
Nicola De Rosa
maturità 2015
QUESTIONARIO
1. Determinare l’espressione analitica della funzione y=f(x) sapendo che la retta y=-2x+5 è
tangente al grafico di f nel secondo quadrante e che f’(x)=-2x2+6.
2. Dimostrare che il volume del tronco di cono è espresso dalla formula:
,
dove R e r sono i raggi e h l’altezza.
n 1
n 1
21
3. Risolvere l’equazione: 5
5
4
4. Un solido ha per base la regione R del piano cartesiano compresa tra il grafico della
1
funzione y 2
e l’asse delle x nell’intervallo [0, 3]. Per ogni punto P di R, di ascissa x,
x 1
l’intersezione del solido col piano passante per P e ortogonale all’asse delle x è un rettangolo
di altezza 3x. Calcolare il volume del solido.
5. Calcolare lim 3x 5 3x 2
x
6. Sia f la funzione, definita per tutti gli x reali, da
,
determinare il minimo di f.
7. Detta A(n) l’area del poligono regolare di n lati inscritto in un cerchio C di raggio r,
verificare che
e calcolarne il limite per
.
8. I lati di un triangolo misurano, rispettivamente, 6 cm, 6 cm e 5 cm. Preso a caso un punto P
all’interno del triangolo, qual è la probabilità che P disti più di 2 cm da tutti i tre vertici del
triangolo?
9. Data la funzione
determinare il parametro k in modo che nell’intervallo [0,2] sia applicabile il teorema di
Lagrange e trovare il punto in cui la tesi del teorema assicura l’esistenza.
10. Il grafico della funzione
divide in due porzioni il rettangolo
ABCD avente vertici A(1,0), B(4,0), C(4,2) e D(1,2). Calcolare il rapporto tra le aree delle
due porzioni.
8
www.matematicamente.it
Nicola De Rosa
maturità 2015
SVOLGIMENTO
2
1. Integrando si ottiene: f ( x) (2 x 2 6)dx x 3 6 x C ;
3
la condizione di tangenza con la retta data impone che sia: f ( x) m in un punto del II quadrante,
da cui: 2 x 2 6 2 x 2 4 x 2 (la soluzione positiva è da scartare);
il punto di ascissa 2 sulla retta ha ordinata: y 2(2) 5 9 ; il punto (2,9) appartiene alla
2
47
curva y f (x) se: 9 (8) 6(2) C , da cui: C
.
3
3
2
47
La funzione richiesta pertanto è: f ( x) x 3 6 x
.
3
3
y
2. Consideriamo il tronco come il solido generato dalla
rotazione del trapezio delimitato dal segmento e dall’asse x
R
in figura intorno all’asse x .
r
La retta passante per i punti (0, r ) ed (h, R) ha equazione:
x
h
Rr
y
x r ; il volume si calcola con:
h
h
h R r
Rr
Rr
x r dz
dx
V y 2 dx
x r dx , che con la sostituzione: z
0
0
h
h
h
h R 2
h
h
z dz
(R3 r 3 )
( R r )( R 2 Rr r 2 ) , da cui l’asserto.
diventa: V
r
Rr
3 Rr
3 Rr
2
n 1 5 n 4
n 5.
3. Innanzitutto per avere senso l’equazione deve aversi
n 1 4 n 5
Risolvendo l’equazione si ha:
n 1! 21 n 1! n 1!n n 1 21 n 1!
5!n 4!
4!n 5!
4!n 5!n 4
4!n 5!
n6
n n 1
21 n 2 20n 84 0 n 10 4
n 14
n 4
5
entrambi accettabili in quanto soddisfano la condizione n 5 .
9
www.matematicamente.it
4.
Nicola De Rosa
S x
Una sezione del solido ha area
3
3
V S x dx
0
0
2
3x 5 3x 2 lim
3x
3
dx ln x 2 1
2
x 1
3
0
maturità 2015
3x
x 1
2
pertanto il volume è pari a
3
ln 10 .
2
5. Si ha:
lim
x
lim
x
3x 5 3x 2
3x 5 3x 2
3x 5 3x 2
x
lim
x
3x 5 3x 2
3x 5 3x 2
7
7
0
3x 5 3x 2
6. La funzione è un polinomio di secondo grado; il suo termine in x 2 ha evidentemente
coefficiente positivo ( a 5 ) , quindi il grafico corrispondente è quello di una parabola a concavità
verso l’alto.
x 6 x
Si verifica facilmente (operando la sostituzione:
) che l’equazione y f (x) è
y y
invariante per simmetria rispetto alla retta x 3 , che pertanto rappresenta l’asse di simmetria della
parabola, ove quindi si trova il vertice che è il punto di minimo richiesto, ed è: f (3) 10 .
7. Il poligono è l’unione di n triangoli isosceli di lato obliquo r ed angolo al vertice
di ciascuno di questi vale:
2
. L’area
n
1 2
2
1
2
r sin
; l’intero poligono ha area: nr 2 sin
.
2
n
2
n
1 2
2
2
nr sin
con la sostituzione: x
diventa:
n 2
n
n
1 2
sin x
sin x
lim r 2
sin x lim r 2
r 2 , avendo fatto uso del limite notevole: lim
1.
x
0
x0 2
x
0
x
x
x
Il limite: lim
10
www.matematicamente.it
Nicola De Rosa
maturità 2015
8. La somma dei tre settori circolari equivale a un settore
circolare di ampiezza 180° pertanto la sua area sarà S A B C
1
r 2 2 .
2
A
2
119
5
Il trinagolo ha altezza h 6
pertanto la sua area è
2
2
2
5 119
.
4
La probabilità richiesta vale:
S ABC
B
C
5 119
2
8
4
1
0.539 54% .
5 119
5 119
4
S
S A B C
p ABC
S ABC
9. Le ipotesi del teorema di Lagrange richiedono continuità in 0,2 e derivabilità in
0,2 .
Per la continuità dev’essere: lim f ( x) lim f ( x) f (1) lim x 3 lim ( x 2 kx k ) 1 , da cui:
x1
x1
x1
x1
1 1 k k 1 , il che è vero per k .
Per la derivabilità: lim f ( x) lim f ( x) lim 3x 2 lim (2 x k ) 3 2 k
x1
x1
x1
x1
da cui:
k 1 .
3
se 0 x 1
x
Pertanto è: f ( x) 2
.
x x 1 s e 1 x 2
L’ascissa x0 prevista dal teorema è quella per cui: f ( x0 )
f (2) f (0)
f (2) f (0) 5
.
, dove:
20
20
2
Prendendo la derivata del primo tratto di funzione, si ottiene: 3x 2
accettabile soltanto la soluzione
x0
5
5
x
di cui è
2
6
5
; operando in modo analogo sul secondo tratto, si
6
5
3
x , non accettabile in quanto non compresa nell’intervallo ]1,2] .
2
4
10. L’area del rettangolo vale 6; di questo, la parte compresa tra la curva assegnata e l’asse delle
ascisse ha area data da:
trova: 2 x 1
4
1
4
14 4
2
14
x dx x x
; la rimanente parte di rettangolo ha dunque area: 6 ed il rapporto
3 3
3
3
1
richiesto vale pertanto
7
.
2
11











