Integrale Definito. (1)
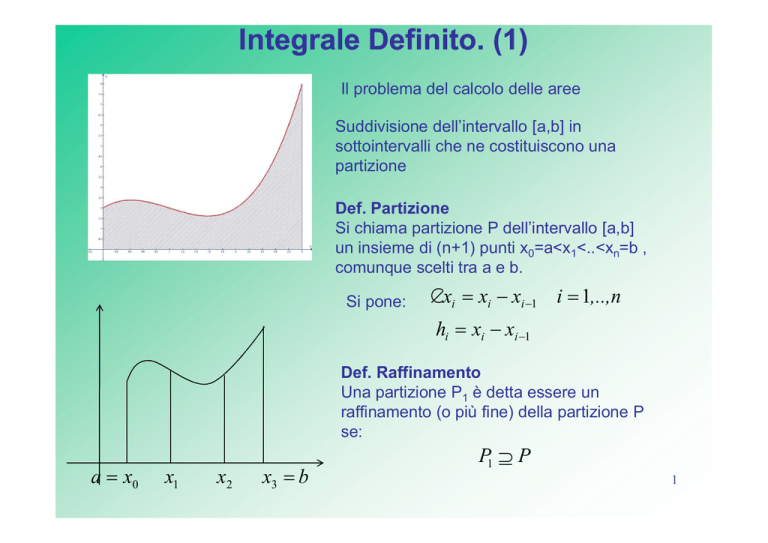
Il problema del calcolo delle aree
Suddivisione dell’intervallo [a,b] in
sottointervalli che ne costituiscono una
partizione
Def. Partizione
Si chiama partizione P dell’intervallo [a,b]
un insieme di (n+1) punti x0=a<x1<..<xn=b ,
comunque scelti tra a e b.
Si pone:
∆xi = xi − xi −1 i = 1,..,n
hi = xi − xi −1
Def. Raffinamento
Una partizione P1 è detta essere un
raffinamento (o più fine) della partizione P
se:
a = x0
x1
x2
x3 = b
P1 ⊇ P
1
Integrale Definito: Plurirettangoli
Assumiamo che la funzione f sia limitata nell’intervallo [a,b].
Data una determinata partizione P di [a,b] consideriamo per ogni intervallino ∆xi :
• mi = l’estremo inferiore assunto dalla funzione in ∆xi
• Mi = l’estremo superiore assunto dalla funzione in ∆xi
Costruiamo il rettangolo inscritto:
di base ∆xi ed altezza mi
Ed associamo ad esso l’ ”area” (che può anche
essere negativa se lo è la funzione) data da:
(∆xi mi).
L’insieme dei rettangoli inscritti costituirà il
plurirettangolo (o scaloide) inscritto.
a = x0
x1
x2
x3 = b
Costruiamo il rettangolo circoscritto:
di base ∆xi ed altezza Mi
Ed associamo ad esso l’ ”area” (che può anche
essere negativa se lo è la funzione) data da:
(∆xi Mi).
L’insieme dei rettangoli inscritti costituirà il
plurirettangolo (o scaloide) circoscritto. 2
Integrale Definito: Somme Superiori ed Inferiori (1)
Def. Somme Superiori
S ( P, f ) = ∑ M i ⋅ ∆xi
i
Costituiscono un’approssimazione “per eccesso”
dell’area
Def. Somme Inferiori
s ( P, f ) = ∑ mi ⋅ ∆xi
i
Costituiscono un’approssimazione “per difetto”
dell’area
a = x0
x1
x2
x3 = b
Abbiamo che:
s ( P, f ) ≤ S ( P, f ) (1)
E’ evidente che con più “raffiniamo” la partizione dell’insieme [a,b] , con più riusciremo
ad avere una valutazione precisa dell’area.
Precisamente, passando da una partizione P ad una partizione più fine P1 notiamo che
le somme inferiori aumentano mentre quelle superiori diminuiscono rispettando sempre
la relazione (1). Quindi:
s ( P, f ) ≤ s ( P1 , f )
se P1 ⊇ P ⇒
(2)
S ( P1 , f ) ≤ S ( P, f )
con
s( P1 , f ) ≤ S ( P1 , f )
3
Integrale Definito: Somme Superiori ed Inferiori (2)
Aumentando il numero di punti le somme inferiori aumentano
Aumentando il numero di punti le somme superiori diminuiscono
4
Integrale Definito di Riemann
Riemann:: Costruzione
Poiché le somme inferiori sono sempre minori od
uguali alle somme superiori, abbiamo che:
Sup s ≤ Inf S
P
P
Def. Funzione Integrabile (secondo Riemann)
La funzione f è integrabile (secondo Riemann, o
R-integrabile) se (e solo se):
a = x0
x1
x2
Sup s = Inf S
x3 = b
P
P
Def. Integrale Definito (di Riemann)
Il numero reale precedentemente trovato rappresenta l’integrale definito della
b
funzione f sull’intervallo [a,b] e si scrive:
∫ f ( x)dx
a
Nota. La classe delle somme inferiori e delle somme superiori sono due classi di numeri
reali una minore dell’altra dunque sono classi separate. Esse possono avere un
elemento separatore (l’unico numero compreso tra le somme inferiori e quelle superiori).
Se tale numero esiste la funzione è detta Riemann-Integrabile (o R-Integrabile) su [a,b]
5
e tale numero è, per definizione , l’integrale di Riemann della funzione data su [a,b].
Integrale Definito di Riemann
Riemann:: Osservazioni
b
∫ f ( x)dx
a
a e b sono detti “estremi di integrazione”
a è detto “estremo inferiore” di integrazione
b è detto “estremo superiore” di integrazione
f è detta funzione integranda
Nota. La variabile di integrazione è una variabile “muta”. Per cui le seguenti espressioni
indicano sempre lo stesso numero:
b
b
b
a
a
a
∫ f ( x)dx ∫ f (t )dt ∫ f ( y)dy
Teorema 1
Una funzione f limitata su [a,b] è R-integrabile se esiste una partizione P di [a,b] tale
che:
∀ε > 0
S(P,f)-s(P,f) < ε
Nota. Il teorema precedente afferma che le somme inferiori e superiori, per funzioni Rintegrabili, sono due classi separate ma indefinitamente ravvicinate (o contigue).
6
Funzione non RR-Integrabile
Nota. Non tutte le funzioni sono R-integrabili. Daremo più avanti delle condizioni
sufficienti affinché una funzione sia R-Integrabile. Occupiamoci di un esempio di
funzione che NON è R-integrabile:
0
f ( x) =
1
La Funzione di Dirichlet
se x ∈ Q
se x ∈ R\Q
Si consideri l’intervallo [0,1].
Essa è una funzioni limitata.
Per essa, considerato il fatto che qualunque sia la partizione P, nell’intervallino ∆xi
compaiono infiniti numeri irrazionali ed infiniti razionali, avremo:
S ( P, f ) = ∑ M i ∆xi = ∑1 ⋅ ∆xi = 1
i
Siccome:
s ( P, f ) = ∑ mi ∆xi = ∑ 0 ⋅ ∆xi = 0
i
Inf S ( P, f ) = 1
i
i
Sup s ( P, f ) = 0
La funzione non risulta R-integrabile.
7
Integrale Definito: le somme di Riemann
Nota. Considerando funzioni limitate non possiamo affermare che i valori mi ed Mi sono
valori assunti dalla funzioni nell’intervallino ∆xi .
Se la funzione f è continua il teorema di Weierstrass assicura il fatto che la funzione
assume in ∆xi tali valori, che coincidono con il minimo ed il massimo della funzione
stessa (in ∆xi).
Al posto delle somme inferiori e superiori è allora possibile considerare le seguenti
somme di Riemann:
σ ( P, f ) = ∑ f (ti )∆xi con ti ∈ ∆xi
Def.
i
P = Max(∆xi )
Per esse vale il seguente teorema:
Teorema 2
f é R - integrabile ⇔ lim σ ( P, f ) = finito
|P|→0
b
E vale
∫ f(x)dx = lim σ(P,f)
a
|P|→0
8
Integrale Definito: Significato Geometrico. (1)
Se la funzione integranda è positiva su [a,b] (a<b) allora
b
∫ f ( x)dx
a
Rappresenta l’area della regione di piano delimitata
dall’asse delle x , dal grafico della funzione e dalle
rette verticali x=a ed x=b. E risulta:
b
∫ f ( x)dx > 0
a
−
+
Se la funzione integranda è negativa su [a,b] (a<b) allora
b
∫ f ( x)dx
a
Rappresenta l’area della regione di piano in senso
algebrico (in quanto negativa) delimitata dall’asse
delle x , dal grafico della funzione e dalle rette
verticali x=a ed x=b. E risulta:
b
∫ f ( x)dx < 0
a
9
Integrale Definito: Significato Geometrico. (2)
b
Se la funzione integranda non ha segno fisso su
[a,b] (a<b) allora l’integrale definito può essere
positivo, negativo o nullo.
∫ f ( x)dx
a
b
∫ f ( x)dx ?
a
2
1
1
−
∫0 1 + x 2 2 dx = .. = arctan(2) − 1 ~ 0.107 > 0
+
2π
∫ sen( x)dx = 0
−
0
+
π
+
∫ cos( x)dx = 0
0
−
−
10
Integrale Definito: Significato Geometrico. (3)
b
∫
a
b
f ( x)dx − ∫ g ( x)dx
Può essere pensato come area della regione di
piano compresa tra le due funzioni f e g.
a
1
∫
f ( x) = − x( x − 2)
0
1
f ( x)dx − ∫ g ( x)dx = .. =
0
1
3
g ( x) = x 2
11
Integrale Definito: Condizioni Sufficienti
per la RR-Integrabilità. (1)
Teorema 3. Se la funzione f è continua su [a,b] allora f è R-Integrabile.
Dim.
Per il teorema di Weierstrass f ammette massimo Mi e minimo mi in ogni
intervallino ∆xi .
Esistono quindi in ∆xi due punti ti e t*i tali che f(ti)=mi e f(t*i)=Mi . Poiché f è
continua, dalla definizione di limite abbiamo che:
ε
Scelto:
b−a
∃δ : se ti − ti* < δ ⇒ f (ti ) − f (ti* ) <
Facciamo in modo che |P|<δ allora:
(
ε
b−a
)
S ( P, f ) − s ( P, f ) = ∑ (M i − mi )∆xi = ∑ f (ti* ) − f (ti ) ∆xi
(
)
i
= ∑ f (ti* ) − f (ti ) ∆xi <
i
ε
b−a
i
∑ ∆xi =
i
ε
b−a
(b − a ) = ε
Per il teorema 1 la funzione è R-Integrabile.
12
Integrale Definito: Condizioni Sufficienti
per la RR-Integrabilità. (2)
Teorema 4. Se la funzione f è limitata su [a,b] e possiede un numero finito (o al più
una infinità numerabile) di discontinuità allora f è R-Integrabile.
Teorema 5. Se la funzione f è monotona (crescente o decrescente) su [a,b] allora f è
R-Integrabile.
13
Integrale Definito: Proprietà (1)
a
Convenzione
∫ f ( x)dx = 0
b
a
∫ f ( x)dx = − ∫ f ( x)dx
a
a
b
b
∫ dx = b − a
a
Proprietà
di
additività
b
b
b
a
a
a
∫ ( f ( x) + g ( x))dx = ∫ f ( x)dx + ∫ g ( x)dx
Proprietà
di linearità
Proprietà di
omogeneità
b
b
∫ (kf ( x))dx = k ∫ f ( x)dx
a
∀k ∈ R
a
14
Integrale Definito: Proprietà (2)
b
b
∫ f ( x)dx ≤ ∫
a
se
b
∫ f ( x)dx ≤ ∫
f ( x) dx se a < b
a
Proprietà di
additività rispetto
all’intervallo di
integrazione
Proprietà di
monotonia
b
a
f ( x) dx
a
b
c
b
a
a
c
∫ f ( x)dx = ∫ f ( x)dx + ∫ f ( x)dx
f1 ( x) ≤ f 2 ( x) in [a, b] ⇒
b
b
∫ f ( x)dx ≤ ∫ f
1
a
2
( x)dx
a
15
Integrale Definito: Teorema della media integrale
Teorema 6 (della Media Integrale o di Lagrange).
Si consideri la funzione f continua in [a,b]. Allora esiste almeno un punto c
in [a,b] tale che:
b
∫ f ( x)dx = f (c)(b − a)
a
Dim.
Siccome f è continua
è R-integrabile.
Per il teorema di Weierstrass se m ed M sono il minimo ed il massimo
della funzione in [a,b] abbiamo m≤f(x) ≤ M valida per ogni x in [a,b]. Dalla
proprietà di monotonia dell’integrale segue::
b
b
b
∫ mdx ≤ ∫ f ( x)dx ≤ ∫ Mdx ⇒
a
a
a
b
m≤
∫ f ( x)dx
a
(b − a )
b
m(b − a ) ≤ ∫ f ( x) dx ≤ M (b − a ) ⇒
a
b
≤M
∫ f ( x)dx
a
(b − a )
= k con m ≤ k ≤ M
Il teorema di Darboux
assicura che esiste c in
[a,b] tale che f(c)=k
b
∫ f ( x)dx
a
(b − a )
b
= f (c )
Def. Media Integrale
c.v.d.
∫ f ( x)dx
a
(b − a )
16
Integrale Definito: Funzione Integrale
Si consideri la funzione f, R-integrabile su [a,b]. Consideriamo due punti di
[a,b] : x0 ed x. Costruiamo il seguente integrale definito: x
∫ f (t )dt
x0
Consideriamo la funzione che ad ogni numero x (in [a,b]) associa il numero
reale definito dalla relazione precedente: tale funzione è la funzione
Integrale di f in [a,b].
Def. Funzione Integrale
Sia f una funzione R-integrabile su [a,b] si definisce funzione integrale F di f su [a,b]
(con origine in x0)
x
F ( x) =
∫ f (t )dt
x0
17
Integrale Definito: Teorema di Torricelli
Torricelli--Barrow
Teorema 7 (di Torricelli - Barrow)
Sia f una funzione continua su [a,b]. Allora la funzione integrale F di f su [a,b] (con
origine x0) è (continua e) derivabile in per ogni x di [a,b] e vale F’(x)=f(x)
Dim.
Si consideri:
=
x+h
x
x+h
x0
x0
x0
x0
x
∆F = F ( x + h) − F ( x) =
x+h
∫ f (t )dt = f (c) ⋅ h con c ∈ [x,x + h]
∫ f (t )dt − ∫ f (t )dt = ∫ f (t )dt + ∫ f (t )dt =
Applicando il teorema 6 della media integrale.
x
∆F
f (c ) ⋅ h
= lim
= lim f (c) = f ( x)
h →0 h
h→0
h→0
h
F ' ( x) = lim
Per la continuità di f
c.v.d.
La funzione integrale F risulta nelle ipotesi del teorema (continuità di f) una primitiva di f.
In generale si può dimostrare che:
Teorema 8
Se f è R-integrabile allora F è continua
Se f è continua allora F è derivabile
Se f è derivabile allora F è derivabile con derivata continua
18
Integrale Definito: Teorema fondamentale del
calcolo (1)
Teorema 9 (Fondamentale del Calcolo)
Sia f una funzione continua su [a,b]. Sia F una sua primitiva , allora:
b
∫ f ( x)dx = F (b) − F (a)
a
b
Dim.
Si consideri:
x0
b
a
b
a
a
x0
x0
x0
∫ f ( x)dx = ∫ f ( x)dx + ∫ f ( x)dx = − ∫ f ( x)dx + ∫ f ( x)dx =
= − F (a ) + F (b) = F (b) − F (a )
Convenzione
b
∫
c.v.d.
f ( x)dx = [F ( x)]a := F (b) − F (a )
b
a
19
Integrale Definito e funzioni primitive
b
∫
f ( x)dx = [F ( x)]a := F (b) − F (a )
b
a
Nota.
Gli integrali delle funzioni continue possono essere calcolati con le funzioni primitive
(se queste si possono esprimere per via elementare).
Se la funzione integranda non è continua ma solo R-integrabile, la primitiva potrebbe
non esistere perché, ad esempio, non esistono funzioni derivabili che hanno derivate
con discontinuità a salto. Tuttavia può esistere l’integrale.
Es.
1
f (x) = 2
3
per 0 ≤ x < 1
per 1 ≤ x < 2
per 2 ≤ x ≤ 3
3
∫ f ( x)dx = 1 + 2 + 3 = 6
0
Non esiste tuttavia una funzione derivabile in
tutto [0,3] che abbia f(x) come funzione derivata
20
Integrale Definito: Integrazione per parti
b
Teorema 10
∫
b
f ' ( x) g ( x)dx = [ f ( x) g ( x)]a − ∫ f ( x) g ' ( x)dx
b
a
a
Es. Calcolare l’area compresa tra l’asse delle x e il grafico della funzione ln(x) tra
i punti di ascissa 1 e 2
2
2
1
2
ln(
x
)
dx
=
[
x
ln(
x
)
]
−
x
1
∫1
∫1 x dx =
2
= 2 ln(2) − ∫ dx = 2 ln(2) − 1 ~ 0.386
1
21
Integrale Definito: Integrazione per sostituzione
Teorema 11
Siano f:[a,b] R continua, Φ :[a,b] R continua,derivabile,con derivata continua e
con Φ’(x) ≠0 in [a,b]. Allora se g è la funzione inversa di Φ, abbiamo
b
Φ (b )
a
Φ(a)
∫ f ( x)dx = ∫ f ( g (t )) g ' (t )dt
Es.
g (t ) = sen(t ) ⇒ Φ ( x) = arcsen( x)
arcsen (1)
1
∫
1 − x 2 dx =
0
∫
1 − sen 2 (t ) cos(t )dt =
arcsen ( 0 )
arcsen (1) =
π
π
π
π
t + sen(t ) cos(t ) 2 2
=
−
0
=
=
cos
(
t
)
dt
=
∫
2
2
4
0
arcsen ( 0 ) = 0
2
2
Area quarto di cerchio di raggio 1
22
Integrale Definito: Area tra grafici di funzioni
b
A = ∫ [ f ( x) − g ( x)]dx
f (x)
a
a
b
b
a
a
b
A = ∫ f ( x)dx + ∫ g ( x)dx
g (x )
f1 ( x)
f 4 ( x)
a
b
c
d
a
a
b
c
d
f 2 ( x) A = ∫ f1 ( x)dx + ∫ f 2 ( x)dx + ∫ f 3 ( x)dx + ∫ f 4 ( x)dx
f 3 ( x)
d b
c
23
Integrali impropri di 1°
1° specie (1)
Abbiamo sinora parlato di integrali di funzioni limitate (in particolare continue) su
intervalli limitati [a,b]. Esistono delle estensioni sia per funzioni non limitate che per
intervalli non limitati.
Integrazione Funzioni non limitate su intervalli limitati
Integrali IMPROPRI di 1°SPECIE
Si consideri f: (a,b] R non limitata (ad es 1/x in (0,1] ) tale
che f sia R-integrabile su ogni intervallo della forma [a+ε,b]
e tale che :
lim+ f ( x) = ±∞
x →a
Definiamo allora:
b
b
∫ f ( x)dx = εlim ∫ε f ( x)dx (*)
a
→0 +
a+
Se il limite (*) esiste finito allora f si dice integrabile in [a,b] e che l’integrale
IMPROPRIO di 1°SPECIE è convergente
Se il limite (*) è ±∞ allora si dice che l’integrale IMPROPRIO di 1°SPECIE è
divergente
Se il limite (*) non esiste allora si dice che l’integrale IMPROPRIO di 1°SPECIE non
esiste
24
Integrali impropri di 1°
1° specie (2)
Es. Si calcoli:
1
∫
0
1
= lim+
ε →0
∫ε
1
x
1
dx =
x
[
1
dx = lim+ 2 x
ε →0
x
]
1
ε
[
]
= lim+ 2 − 2 ε = 2
ε →0
1
x
1
Es. Si calcoli:
1
∫0 x dx =
1
= lim+ ∫ dx = lim+ [ln x ] 1ε = +∞
ε →0
ε →0
ε x
1
1
1
Es. Si calcoli:
∫0 x k dx = Per k≠1 εlim
→0
+
1
= − k + 1
+ ∞
1
∫ε
1
x − k +1
1
1
ε − k +1
−
dx = lim+
=
= εlim
→0+ − k + 1
ε →0
−
k
+
1
xk
−
k
+
1
ε
se − k + 1 > 0 ⇔ k < 1
se − k + 1 < 0 ⇔ k > 1
Per k=1 vedi es. precedente.
Globalmente:
1
se − k + 1 > 0 ⇔ k < 1
1
∫0 x k dx = 1 − k
se − k + 1 ≤ 0 ⇔ k ≥ 1
+ ∞
1
25
Integrali impropri di 1°
1° specie (3)
b
b
∫ f ( x)dx = εlim ∫ε f ( x)dx (*)
a
→0 +
Ad es. 1/(x-1)2 in [0,1)
a+
Teorema 12
divergente a + ∞ se k ≥ 1
1
1− k
dx
é
(
b
−
a
)
∫a ( x − a) k
se k < 1
convergente =
1− k
b
b
Vale un risultato perfettamente analogo per:
1
∫a (b − x) k dx
L’integrale converge se la funzione è infinita di ordine k<1 altrimenti diverge.
26
Integrali impropri di 1°
1° specie (3)
Analogamente nel caso in cui si abbia:
Si definisce:
lim− f ( x) = ±∞
x →b
b −ε
b
∫ f ( x)dx = εlim ∫ f ( x)dx (**)
a
→0 +
a
Ad es. 1/(x-1)2 in [0,1)
Vale un risultato perfettamente analogo a quello
enunciato nel teorema 12 :
Teorema 12-bis
divergente a + ∞ se k ≥ 1
1
dx
é
(b − a)1− k
∫a (b − x) k
se k < 1
convergente =
1− k
b
L’integrale converge se la funzione è infinita di ordine k<1 altrimenti diverge.
27
Integrale Definito: Integrali impropri di 2°
2° specie (1)
Integrazione Funzioni su intervalli illimitati
Integrali IMPROPRI di 2°SPECIE
Si consideri f: [a,+∞) R continua. Poniamo:
+∞
k
∫ f ( x)dx := lim ∫ f ( x)dx
k → +∞
a
a
Analogamente, se f:(-∞,a] R continua. Poniamo:
a
∫ f ( x)dx := lim ∫ f ( x)dx
k → −∞
−∞
Se f:(-∞,+∞)
a
k
R continua. Poniamo:
+∞
a
+∞
−∞
−∞
a
a
h
∫ f ( x)dx = ∫ f ( x)dx := ∫ f ( x)dx + ∫ f ( x)dx = lim ∫ f ( x)dx + lim ∫ f ( x)dx
R
k → −∞
k
h → +∞
a
28
Integrale Definito: Integrali impropri di 2°
2° specie (2)
Es. Si calcoli:
+∞
∫
1
Es. Si calcoli:
[
k
1
1
lim
dx = lim 2 x
dx =
∫
k → +∞
k → +∞
x
x
1
+∞
]
k
1
[
]
= lim 2 k − 2 = +∞
k → +∞
1
1
k
[
]
dx
=
lim
dx
=
lim
ln
x
1 = lim [ln( k ) ] = +∞
∫1 x k → +∞ ∫1 x
k → +∞
k → +∞
k
+∞
Es. Si calcoli:
k
1
∫1 x 2 dx = klim
→ +∞ ∫
1
k
1
1
1
=
−
dx
lim
=
lim
−
+
1
=1
2
k → +∞
x
x 1 k → +∞ k
Es. Si calcoli (per n≠1):
+∞
+ ∞
= 1
n − 1
se 1 − n > 0 ⇔ n < 1
se 1 − n < 0 ⇔ n > 1
1− n
k
x
k 1− n
1
1
1
=
=
−
lim
dx
lim
lim
dx
=
∫1 x n k → +∞ ∫1 x n
k → +∞ 1 − n
k → +∞ 1 − n
1
−
n
1
k
Per n=1 vedi es.
precedente.
Globalmente:
+∞
+ ∞
se n ≤ 1
1
dx
=
∫1 x n 1 se n > 1
n − 1
L’integrale converge se la funzione è infinitesima di ordine n>1 altrimenti diverge.
29
Integrale Definito: Integrali impropri di 2°
2° specie (3)
Es. Andamento grafico
1
x2
1
x
30
Integrale Definito: Integrali impropri di 2°
2° specie (4)
Es. Si calcoli:
+∞
h
1
h
lim ∫ f ( x)dx = lim lim [arctan( x)]k =
∫−∞1 + x 2 dx = klim
→ −∞ h → +∞
k → −∞ h → +∞
k
π
π
= lim lim [arctan(h) − arctan(k )] = − − = π
k → −∞ h → +∞
2 2
31
Integrale Definito: Lunghezza di una curva (1)
Consideriamo una funzione y=f(x). Sia f una funzione continua con derivata
continua in [a,b]. Vogliamo calcolare la lunghezza della curva rappresentata dal
grafico della funzione tra i punti di ascissa a e b.
Per incrementi infinitesimi della variabile x ( da x a x+dx) la variabile y ha un
incremento dy che possiamo approssimare con dy=f’(x)dx (differenziale). Allora la
lunghezza infinitesima della curva dl può essere scritta attraverso il teorema di
Pitagora:
dl =
(dx )2 + (dy )2
=
(dx )2 + ( f ' ( x)dx )2
[
= dx 1 + ( f ' ( x) )
2
]
2
dl = 1+ f ( x) dx
Ne segue:
b
f ( x + dx)
f (x)
'
lunghezza = ∫ 1 + ( f ' ( x) ) dx
2
dy
dl
a
dx
32
x x + dx
Integrale Definito: Lunghezza di una curva (2)
Es. Lunghezza Circonferenza ( di raggio R)
f ( x) = R − x f ' ( x) = −
2
R
R
l = 4∫ 1 + ( f ' ( x) ) dx = 4 ∫
2
0
R
= 4R∫
0
0
R
1
x
R 1−
R
2
dx = 4 R ∫
0
R2 − x2
2
Es. Lunghezza Arco di Parabola
f ' ( x) = 2 x
f ( x) = x 2
R
R
x
= 4∫
dx =
1+ 2
dx
2
2
R −x
0
R − x2
2
1
1− t
La lunghezza della circonferenza
( di raggio R) vale:
x
2
dt = 4 R[arcsen(t )]10 = 4 R[arcsen(1) − arcsen(0)] = 4 R
1
1
l = ∫ 1 + ( f ' ( x) ) dx = ∫
2
0
0
2
= 2πR
2
1
1 + 4 x 2 dx = ∫ 1 + y 2 dy
20
2
1 y 1 + y + SettSh( y )
2 5 + ln(2 + 5 )
=
~ 1.478943
=
2
2
4
0
2
π
33
Integrale Definito: Lunghezza di una curva (3)
Es. Lunghezza Catenaria ( curva lungo la quale si dispone una fune pesante omogenea,
nel campo di gravità, fissata agli estremi).
f ( x) = Ch( x)
a
l=
∫
−a
f ' ( x) = Sh( x)
a
1 + Sh 2 ( x) dx = ∫ Ch( x)dx =
−a
= Sh(a) − Sh(−a ) = 2 Sh(a) = e a − e − a
34
Integrale Definito: Superficie solidi di rotazione (1)
La superficie del solido di rotazione viene
calcolata come somma (integrale) delle
superfici laterali dei tronchi di cono infinitesimi
di altezza dx.
La superficie laterale di un tronco di cono vale:
dl
f (x)
a
b
x
S lat = πa ( R + r )
Essendo a l’apotema ed R, r i raggi delle basi.
dx
Il primo teorema di Pappo-Guldino assicura che il calcolo della superficie di rotazione
può essere attuato moltiplicando la lunghezza del segmento dl (che genera la superficie
di rotazione) per la lunghezza della circonferenza che il baricentro del segmento
percorre durante la rotazione. Perciò:
dS lat = 2πf ( x)dl
b
b
a
a
[
]
S lat = 2π ∫ f ( x)dl = 2π ∫ f ( x) 1 + f ' ( x) dx
2
35
Integrale Definito: Superficie solidi di rotazione (2)
Es. Superficie Sfera
y = f ( x) = R − x
2
R
2
f ' ( x) = −
S sfera
x
R2 − x2
R
= 2 2π ∫ R 2 − x 2
0
S sfera
[
]
2
1 + f ' ( x) =
R
R2 − x2
dx =
2
2
R −x
R
R
= 4πR ∫ dx = 4πR 2
0
36
Integrale Definito: Volumi solidi di rotazione (1)
Il volume del solido viene costruito come
somma (integrale) di cilindretti infinitesimi si
“spessore” (altezza) dx e superficie di base
π [f(x)]2.
f (x)
a
b
dx
dV = π [ f ( x )] dx
2
b
V = π ∫ [ f ( x)] dx
2
a
Es. Volume Cono
retta : y = f(x) =
P ≡ ( h, R )
2
R
x
h
h
R x
1
R
V = π ∫ x 2 dx = π 2 = πR 2 h
h
h 3 0 3
0
h
h
2
3
1 2
V = πR h
3
37
Integrale Definito: Volumi solidi di rotazione (1)
Es. Volume Sfera
y = f ( x) = R − x
2
Vsfera
2
2
R
R 2
x
2
2
= 2 π ∫ R − x dx = 2πR ∫ 1 − dx =
0
0
R
(
)
x
y
=
R
dy = 1 dx
R
R
[
]
1
y
4 3
3 2
= 2πR ∫ 1 − y dy = 2πR y − = 2πR = πR
3 0
3 3
0
1
3
2
3
3
38
Studio Funzione f1
Fare il grafico qualitativo della funzione e calcolare il valore dell’integrale nel tratto
3≤x≤2 3
x3
y = f ( x) = 2
x −1
Asintoti verticale : x=-1 e x=1
(
x2 x2 − 3
y' = 2
( x − 1) 2
)
Asintoti Obliquo : y=x
(
2x x2 + 3
y' ' = 2
( x − 1) 2
)
x3
x
dx
=
xdx
+
∫ x2 −1 ∫
∫ x 2 − 1 dx =
x2 1
=
+ ln x 2 − 1 + c
2 2
∫
2 3
3
x3
dx =
2
x −1
x
2
2
2 3
3
[
1
+ ln x 2 − 1
2
]
2 3
3
12 − 3 1
9
11
=
+ [ln(11) − ln(2)] = + ln
≅ 5,35
2
2
2
2
Studio Funzione g1
Fare il grafico qualitativo della funzione seguente e calcolare il valore dell’integrale
nel tratto 0≤x ≤ 1
x
y = e −1
ex
y' =
Punto a tangente verticale nell’origine
2 e −1
1 e x (e x − 2)
y' ' =
Flesso per x=ln(2)
x
x
4 2(e − 1) e − 1
x
∫
∫
e x − 1dx
t = e x − 1
ex
t 2 +1
dx
dt = dx =
2t
2t
2t
2t 2
e − 1dx = ∫ t 2
dt = ∫ 2
dt =
t +1
t +1
x
t 2 + 1 −1
1
= 2∫ 2
dt =2∫ dt − 2∫ 2 dt =2t − 2 arctan(t ) + c =
t +1
t +1
= 2 e x − 1 − 2 arctan( e x − 1) + c
Studio Funzione g1
Fare il grafico qualitativo della funzione seguente e calcolare il valore dell’integrale
nel tratto 0≤x ≤ 1
x
y = e −1
1
∫
0
[
] [
]
x
1
x
1
e x − 1dx = = 2 e − 1 0 − 2 arctan( e − 1) 0 =
[
] [
]
= 2 e1 − 1 − 2 arctan( e1 − 1) ≅ 0,78










