La parabola - videolezioni.org

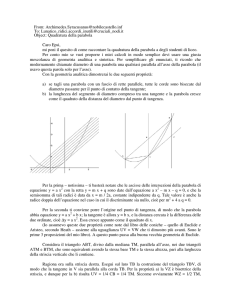
La parabola
c
Copyright 2008
Pasquale Terrecuso
Tutti i diritti sono riservati.
La parabola di equazione y = ax2 + bx + c
2
Concavità . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Se ‘a’ varia... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Simmetria . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Asse di simmetria . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
Vertice . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Intersezione con assi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
Se ‘c’ varia... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
Se ‘b’ varia... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
Esercizio riassuntivo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
Disequazione di II grado e Segno del trinomio
18
Disequazione di II grado . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Segno del trinomio . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
Definizione di parabola
28
La parabola come conica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
La parabola come luogo geometrico. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
Il fuoco . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
Intersezioni della parabola con altre curve del piano
33
Intersezioni parabola-retta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
Intersezioni parabola-parabola . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
Intersezioni parabola-circonferenza . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
Tangenti ad una parabola
37
1
La parabola di equazione y = ax2 + bx + c
Il grafico della parabola di equazione y = ax2 + bx + c
I passi fondamentali che conducono ad un disegno della parabola di equazione
y = ax2 + bx + c
che contiene gli elementi essenziali sono i seguenti:
1. segno di a (verso della concavità)
2. asse di simmetria
3. vertice (minimo per a > 0, massimo per a < 0)
4. intersezione con l’asse x
5. intersezione con l’asse y
Discuteremo come esempio particolare il grafico della parabola di equazione:
y = x2 − 5x + 4
Prof. P. Terrecuso –
La parabola
Il segno di ‘a’ ovvero il verso della concavità
Per a > 0 la concavità è rivolta verso l’alto; per a < 0 la concavità è rivolta verso il basso:
y = x2
5
4
3
2
1
y = −x2
y
x
−4
−3
−2
−1−1
−2
−3
−4
−5
−6
1
2
3
Prof. P. Terrecuso –
La parabola
2
Il segno di ‘a’ ovvero il verso della concavità
y = x2 − 2x
y = −x2 + 4
a = +1 > 0 la concavità è rivolta verso l’alto;
a = −1 < 0 la concavità è rivolta verso il basso:
5
4
3
2
1
y
x
−4
−3
−2
−1−1
−2
−3
−4
−5
−6
1
2
3
Prof. P. Terrecuso –
La parabola
Se ‘a’ varia...
Cambia l’ampiezza dell’apertura e la concavità.
In particolare:
● Per valori positivi ma decrescenti di ‘a’, la parabola diventa via via più allargata e
meno piccata intorno al suo asse di simmetria
● fino a diventare piatta cioè una retta per a = 0
● per poi cambiare concavità verso il basso per a < 0,
● al crescere del valore assoluto di ‘a’ la parabola ridiventa sempre più stretta e piccata
intorno al suo asse di simmetria
Prof. P. Terrecuso –
La parabola
3
Simmetria e asse di simmetria
Una simmetria di una figura geometrica è una trasformazione che lascia la figura invariata.
Una trasformazione può essere per esempio una rotazione nel piano intorno ad un’asse
perpendicolare alla figura stessa. In questo caso vi è un punto della figura che rimane fisso detto
centro della simmetria.
Se i punti fissi formano una retta (come in una riflessione nel piano, o una rotazione nello
spazio) questa è detto asse della simmetria.
5
4
3
2
1
-2
-1
0
La parabola
1
2
3
4
5
6
7
8
9
10
11
Prof. P. Terrecuso –
La determinazione dell’asse di simmetria
L’asse di simmetria della parabola y = ax2 + bx + c ha equazione:
x=
−b
2a
5
4
3
2
1
0
-2
-1
0
La parabola
1
2
3
4
5
6
7
4
8
9
10
11
Prof. P. Terrecuso –
Asse di simmetria per parabole della forma y = ax2 + c
Per b = 0 l’asse di simmetria della parabola ha equazione:
x=0
5
cioè coincide con l’asse delle ordinate.
4
3
2
1
0
-2
-1
0
La parabola
1
2
3
4
5
6
7
8
9
10
11
Prof. P. Terrecuso –
Il vertice ovvero il minimo o il massimo della parabola
Il vertice è il punto di intersezione tra la parabola e l’asse di simmetria.
5 Si tratta di un minimo per a > 0 e un massimo per a < 0.
4
3
2
1
0
-1
-2
-1
0
La parabola
1
2
3
4
5
6
7
5
8
9
Prof. P. Terrecuso –
Il vertice ovvero il minimo o il massimo della parabola
5
Le coordinate
del vertice V della parabola (xv , yv ) sono date da:

−b


xv = 2a
2


yv = −b + 4ac = −∆
4a
4a
4
3
2
1
0
-2
-1
0
La parabola
1
2
3
4
5
6
7
8
9
Prof. P. Terrecuso –
Intersezione con gli assi
Intersezione con l’asse x:
(
y = ax2 + bx + c
equazione dell′ asse x
Intersezione con l’asse y:
(
y = ax2 + bx + c
equazione dell′ asse y
Prof. P. Terrecuso –
La parabola
6
Intersezione
con l’asse x
(
y = ax2 + bx + c
y=0
5
4
3
2
1
0
-1
-2
-1
0
La parabola
1
2
3
4
5
6
7
8
9
4
5
6
7
8
9
Prof. P. Terrecuso –
Intersezione
con l’asse y
(
y = ax2 + bx + c
x=0
5
4
3
2
1
0
-1
-2
-1
0
La parabola
1
2
3
7
Prof. P. Terrecuso –
Se ‘c’
( varia...
y = ax2 + bx + c
x=0
Si deduce che il punto di intersezione con l’asse y è di coordinate
(0, c).
Inoltre essendo le coordinate del vertice
(
−b
−b2
,c +
)
2a
4a
ne deriva che al variare di c la parabola si sposta verticalmente.
Prof. P. Terrecuso –
La parabola
Se ‘b’ varia...
Essendo le coordinate del vertice V (xv , yv ) della parabola di equazione y = ax2 + bx + c :

−b



xv = 2a
2

−b2
b


+ c = −a
+ c = −ax2v + c
y v =
4a
2a
fissato ‘a’ e ‘c’ ne deriva che al variare di ‘b’ il vertice della parabola si sposta muovendosi
su una parabola di equazione
yv = −ax2v + c
Prof. P. Terrecuso –
La parabola
8
Esercizio
riassuntivo
Disegniamo il grafico
della parabola di equazione
y = x2 − 5x + 4
5
4
3
2
1
0
-1
-2
-2
-1
0
La parabola
1
2
3
4
5
6
7
8
9
10
11
Prof. P. Terrecuso –
Disequazione di II grado e Segno del trinomio
La parabola e le disequazioni di II grado
Risolvere
ax2 + bx + c > 0
posto
y = ax2 + bx + c
equivale a chiedersi per quali valori della x il grafico della parabola si trova sopra l’asse
delle ascisse?
y
5
4
3
2
1
x
−4
−3
−2
−1−1
−2
−3
1
2
3
Prof. P. Terrecuso –
La parabola
9
La parabola e le disequazioni di II grado
Risolvere
−x2 + 4 > 0
posto
y = −x2 + 4
equivale a chiedersi per quali valori della x il grafico della parabola si trova sopra l’asse
delle ascisse?
y
5
4
3
2
1
x
−4
−3
−2
−1−1
−2
−3
1
2
3
Prof. P. Terrecuso –
La parabola
La parabola e le disequazioni di II grado
Risolvere
ax2 + bx + c < 0
posto
y = ax2 + bx + c
equivale a chiedersi per quali valori della x il grafico della parabola si trova sotto l’asse
delle ascisse?
y
5
4
3
2
1
x
−4
−3
−2
−1−1
−2
−3
1
2
3
Prof. P. Terrecuso –
La parabola
10
La parabola e le disequazioni di II grado
Risolvere
−x2 + 4 < 0
posto
y = −x2 + 4
equivale a chiedersi per quali valori della x il grafico della parabola si trova sotto l’asse
delle ascisse?
y
5
4
3
2
1
x
−4
−3
−2
−1−1
−2
−3
1
2
3
Prof. P. Terrecuso –
La parabola
La parabola e le equazioni di II grado
Risolvere
ax2 + bx + c = 0
posto
y = ax2 + bx + c
equivale a chiedersi per quali valori della x il grafico della parabola interseca l’asse delle
ascisse?
y
5
4
3
2
1
x
−4
−3
−2
−1−1
−2
−3
1
2
3
Prof. P. Terrecuso –
La parabola
11
La parabola e le equazioni di II grado
Risolvere
x2 − 4 = 0
posto
y = x2 − 4
equivale a chiedersi per quali valori della x il grafico della parabola interseca l’asse delle ascisse?
5
4
3
2
1
y
x
−4
−3
−2
−1−1
−2
−3
−4
1
2
3
Prof. P. Terrecuso –
La parabola
La parabola e lo studio del segno del trinomio
y = ax2 + bx + c
con
a>0
x
∆>0
∆=0
x
∆<0
x
Prof. P. Terrecuso –
La parabola
12
La parabola e lo studio del segno del trinomio
y = ax2 + bx + c
a<0
con
∆>0
x
∆=0
x
∆<0
x
Prof. P. Terrecuso –
La parabola
La parabola e lo studio del segno del trinomio: un esempio
y = ax2 + bx + c
5
y = x2 − 5x + 4
4
3
2
1
0
-1
-2
-2
-1
0
La parabola
1
2
3
4
5
6
13
7
8
9
Prof. P. Terrecuso –
Definizione di parabola
La parabola come conica
Prof. P. Terrecuso –
La parabola
La parabola come luogo geometrico
In matematica, ed in particolare in geometria, un luogo geometrico, o, più
semplicemente, un luogo, è l’insieme di tutti e soli i punti del piano o dello spazio
che hanno in comune una determinata proprietà.
La parabola è il luogo dei punti del piano equidistanti da un punto detto fuoco
e da una retta detta direttrice della parabola.
Prof. P. Terrecuso –
La parabola
14
La parabola, il fuoco e la direttrice
La parabola è il luogo dei punti del piano equidistanti da un punto detto fuoco F (xF , yF ) e da
una retta detta direttrice della parabola.
4
3
2
1
0
-1
-2
-2
-1
0
1
2
3
4
5
6
7
8
9
Prof. P. Terrecuso –
La parabola
5 Una
proprietà del fuoco
4
3
2
1
0
-1
-2
-2
-1
0
La parabola
1
2
3
4
5
6
15
7
8
9
Prof. P. Terrecuso –
Intersezioni della parabola con altre curve del piano
Intersezioni di una parabola con una retta
3
(
y = ax2 + bx + c
y = mx + n
2
1
0
-1
-2
-2
-1
0
La parabola
1
2
3
4
5
6
7
8
9
5
6
7
8
9
Prof. P. Terrecuso –
Intersezioni di due parabole
3
(
y = a1 x 2 + b 1 x + c 1
y = a2 x 2 + b 2 x + c 2
2
1
0
-1
-2
-2
-1
0
La parabola
1
2
3
4
16
Prof. P. Terrecuso –
Intersezioni di una parabola con una circonferenza
4
(
y = ax2 + bx + c
x2 + y 2 + mx + ny + p = 0
3
2
1
0
-1
-2
-1
0
La parabola
1
2
3
4
5
6
7
8
9
Prof. P. Terrecuso –
Tangenti ad una parabola
Tangenti ad una parabola
● Tangenti ad una parabola per un punto esterno
● Tangenti ad una parabola per un punto appartenente alla parabola
● Tangenti ad una parabola per un punto interno
Prof. P. Terrecuso –
La parabola
17
Tangenti ad una parabola
5
● Tangenti ad una parabola per un punto esterno
4
3
2
1
0
-1
-2
-2
-1
0
La parabola
1
2
3
4
5
6
7
8
9
Prof. P. Terrecuso –
Tangenti ad una parabola
● Tangenti ad una parabola per un punto appartenente alla parabola
5
4
3
2
1
0
-1
-2
-1
0
La parabola
1
2
3
4
5
6
18
7
8
9
Prof. P. Terrecuso –
Tangenti
ad una parabola
● Tangenti ad una parabola per un punto interno
5
4
3
2
1
0
-1
-2
-2
-1
0
La parabola
1
2
3
4
5
6
19
7
8
9
Prof. P. Terrecuso –