Corso di Chimica Fisica A Prove d`esame

Università di Torino
Corso di Studi in Chimica - Laurea Triennale
A. A. 2005-2006
Corso di Chimica Fisica A
Prove d’esame
Roberto Dovesi
Bartolomeo Civalleri
/home/mimmo/testitex/tut cf-a 06/esami cfa 06.pdf (11 April 2006)
1
CORSO DI LAUREA IN CHIMICA - ANNO ACCADEMICO 2005-06
PROVA DELL’ESAME DI CHIMICA FISICA A
March 29, 2006
Regole per lo svolgimento dell’esame
1) barrare gli esercizi che si sono svolti;
2) scrivere qui sotto in quale pagina si trova l’esercizio svolto;
3) separare nettamente, con una riga, la fine di un esercizio dall’inizio di un altro;
4) mettere nome e cognome su ogni foglio;
5) sottolineare il risultato finale.
Cognome: ..................................................
Nome: ........................................
Data di nascita: ........................................
Firma: ........................................
N. di Matricola: ...........................
Parte obbligatoria
1. Dimostrare che ∆U è nulla per un gas ideale che subisce prima un’espansione isoterma da A(P 1 , V1 , T1 ) a
B(P2 , V2 , T1 ), poi un riscaldamento isocoro da B(P2 , V2 , T1 ) a C(P1 , V2 , T2 ) e infine un raffreddamento isobaro
da C(P1 , V2 , T2 ) a A(P1 , V1 , T1 ). Rappresentare il processo termodinamico attraverso un diagramma P V e commentare il risultato.
2. Esprimere il fattore di compressibilità usando l’equazione di van der Waals (troncare al secondo ordine).
Quale è il valore di Z per una mole di CO2 che occupa un volume di 100.0 dm3 a 273.15 K? Che tipo di forze
prevalgono? (Usare: a = 3.6551 dm6 ·bar·mol−2 e b = 0.042816 dm3 ·mol−1 ).
3. Calcolare il lavoro w fatto dal sistema durante una espansione isoterma reversibile di una mole di un gas che
si comporta secondo la seguente equazione di stato:
P =
nRT
V − nb
e che a T = 100 K passi da Vi = 20.0 dm3 a Vf = 60.0 dm3 . Considerare b = 0.038577 dm3 ·mol−1 .
4. A che temperatura deve lavorare la sorgente calda per avere un rendimento del 25% se la sorgente fredda si
trova a 25◦ C? A questo punto, se si fissa la temperatura della sorgente calda a che temperatura deve trovarsi
la sorgente fredda per aumentare il rendimento al 40%? Commentare i risultati.
5. Come dipende l’entalpia di una reazione dalla temperatura?
Data la reazione di combustione dell’acido benzoico
C7 H6 O2 (l) + 15/2 O2 (g) → 7 CO2 (g) + 3 H2 O(l)
Assumendo che le capacità termiche molari dei prodotti e dei reagenti siano costanti nell’intervallo di temperatura tra 290 K e 320 K e sapendo che ∆Hr (298K) = -3250.1 kJ/mol e ∆Hr (313K) = -3248.2 kJ/mol, calcolare
la variazione della capacità termica tra 298 K e 313 K.
2
6. Se il ∆Hf0 di CCl4 (l) è -135.4 kJ/mol e il ∆Hf0 di CCl4 (g) è di -102.9 kJ/mol, quanto è il calore richiesto
per vaporizzare due moli di CCl4 (l) a 298 K?
7. Il seguente differenziale
nRT
dV
V
è esatto o inesatto? Considerare CV una semplice funzione di T .
Che cosa si può dire di x/T ? C’è una funzione di stato termodinamica che si comporta in questo modo?
dx = CV dT +
8. Dite tutto quello che vi ricordate sul secondo principio della termodinamica.
9. Il calore di transizione dalla fase α alla fase β per il ferro è, alla temperatura di transizione, pari a 1.715
kJ/(g·atomo). La variazione di entropia relativa alla trasformazione è di 1.660 J/(K·g·atomo). Quale è la temperatura di transizione?
10. Ricavare la relazione di Maxwell corrispondente a dU = T dS − P dV .
Parte facoltativa
11. Nell’ipotesi di comportamento tipo van der Waals, quale membro in ciascuna delle seguenti coppie è più
probabile che devii dal comportamento ideale?
a) H2 rispetto a monossido di carbonio
b) Azoto rispetto a O2
Spiegate le vostre scelte.
Aiutatevi tenendo conto che le costanti di van der Waals sono:
gas
H2
N2
O2
CO
a (dm6 ·bar·mol−2 )
0.244
1.390
1.360
1.485
b (dm3 ·mol−1 )
2.661
3.913
3.183
3.985
12. Il coefficiente di espansione termica, α, di una sostanza è definito come
1 ∂V
α=
V ∂T P
(1)
Un liquido che si trova alla temperatuta T1 e volume V1 viene riscaldato da T1 a T2 a pressione costante.
Trovare un’espressione per V2 considerando α indipendente dalla temperatura
13. Si dispongano le seguenti reazioni secondo valori crescenti di ∆Sr0 (senza consultare fonti di riferimento)
(a) 2 H2 (g) + O2 (g) → H2 O(l)
(b) NH3 (g) + HCl(g) → NH4 Cl(s)
(c) K(s) + O2 (g) → KO2 (s)
(d) N2 (g) + 3 H2 (g) → 2 NH3 (g)
3
CORSO DI LAUREA IN CHIMICA - ANNO ACCADEMICO 2005-06
CORREZIONE DELLA PROVA DELL’ESAME DI CHIMICA FISICA A
March 29, 2006
Parte obbligatoria
1. Dimostrare che ∆U è nulla per un gas ideale che subisce prima un’espansione isoterma da A(P 1 , V1 , T1 ) a
B(P2 , V2 , T1 ), poi un riscaldamento isocoro da B(P2 , V2 , T1 ) a C(P1 , V2 , T2 ) e infine un raffreddamento isobaro
da C(P1 , V2 , T2 ) a A(P1 , V1 , T1 ). Rappresentare il processo termodinamico attraverso un diagramma P V e commentare il risultato.
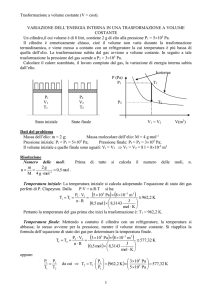
Soluzione
Il diagramma P V corrispondente al processo termodinamico è:
6
P1
Aa
aC
P2
a B
V1
V2
Dalla figura si vede subito che il processo termodinamico completo è ciclico.
A-B) Nel tratto A-B di espansione isoterma ∆UAB = 0 perchè l’energia interna di un gas ideale dipende solo
dalla temperatura che in questo caso è costante.
B-C) Per la trasformazione isocora vale
∆UBC =
Z
T2
∆CV (T )dT
T1
B-A)
∆UCA =
Z
T1
∆CV (T )dT = −
Z
T2
∆CV (T )dT
T1
T2
Sommando i singoli termini,
∆Utot = 0 +
Z
T1
∆CV (T )dT −
T2
Z
T2
∆CV (T )dT = 0
T1
la variazione energia interna totale è nulla, come volevasi dimostrare. U è una funzione di stato e quindi dipende
solo dallo stato termodinamico iniziale e da quello finale. Se i due coincidono, come si ha in un processo ciclico,
la variazione totale è nulla.
2. Esprimere il fattore di compressibilità usando l’equazione di van der Waals (troncare al secondo ordine).
Quale è il valore di Z per una mole di CO2 che occupa un volume di 100.0 dm3 a 273.15 K? Che tipo di forze
4
prevalgono? (Usare: a = 3.6551 dm6 ·bar·mol−2 e b = 0.042816 dm3 ·mol−1 ).
Soluzione
Il fattore di compressibilit dato da:
RT
B2V
=1+
+ ...
Vm
Vm
per un gas che segue l’equazione di stato di van der Waals il secondo coefficiente del viriale vale:
a
B2V = b −
RT
quindi
a 1
Z =1+ b−
·
RT
Vm
sostituendo i dati forniti dall’esercizio si ottiene:
1
3.6551 dm6 · bar · mol−2
·
Z = 1 + 0.042816 dm3 · mol−1 +
= 0.9988
0.083145 dm3 · bar · mol−1 · K −1 273.15 K
100.0 dm3
Z=
Dato che Z<1 prevalgono le forze attrattive, anche se la deviazione dall’idealità è molto piccola.
3. Calcolare il lavoro w fatto dal sistema durante una espansione isoterma reversibile di una mole di un gas che
si comporta secondo la seguente equazione di stato:
P =
nRT
V − nb
e che a T = 100 K passi da Vi = 20.0 dm3 a Vf = 60.0 dm3 . Considerare b = 0.038577 dm3 ·mol−1 .
Soluzione
Il lavoro è dato da δw = −P dV che integrato tra Vi e Vf diventa
Z Vf
w=−
P dV
Vi
Data l’espressione della pressione in funzione del volume, sostituendo P nella relazione sopra e integrando si
ottiene
Z Vf
dV
Vf − nb
w = −nRT
= −nRT ln
V
−
nb
Vi − nb
Vi
allora
w = −1 mol · 8.3145 J · K −1 · mol−1 · 100 K · ln
60.0 dm3 − 0.038577 dm3 · mol−1
w = −915J/mol
20.0 dm3 − 0.038577 dm3 · mol−1
4. A che temperatura deve lavorare la sorgente calda per avere un rendimento del 25% se la sorgente fredda si
trova a 25◦ C? A questo punto, se si fissa la temperatura della sorgente calda a che temperatura deve trovarsi
la sorgente fredda per aumentare il rendimento al 40%? Commentare i risultati.
Soluzione
Il rendimento di una macchina termica è dato dall’espressione
ηmax = 1 −
Tf
Tc
dove Tf e Tc sono rispettivamente le temperature della sorgente fredda e di quella calda.
5
(a) Dalla formula sopra si ricava:
Tc =
Quindi
Tc =
Tf
1 − ηmax
298.15 K
= 397.53 K
1 − 0.25
(b) Fissando Tc = 397.53 K, per avere un rendimento del 40% deve essere
Tf = (1 − ηmax ) · Tc = (1 − 0.4) · 397.53 K = 238.52 K
Il rendimento η di una macchina termica è il rapporto tra il lavoro compiuto e il calore assorbito dalla sorgente
più calda
qrev,c − qrev,f
qrev,f
−w
=
=1+
(2)
ηmax =
qrev,c
qrev,c
qrev,c
T
che è anche uguale a ηmax = 1 − Tfc . Ciò dimostra che per ottenere il massimo rendimento possibile si può
operare in due modi: o si diminuisce la temperatura della sorgente fredda o si utilizza una sorgente calda ad
altissima temperatura. Infatti η → 1 se Tf → 0 o se Tc → ∞. Maggiore è il salto termico tra le due sorgenti,
maggiore è il rendimento che si può ottenere.
5. Come dipende l’entalpia di una reazione dalla temperatura?
Data la reazione di combustione dell’acido benzoico
C7 H6 O2 (l) + 7/2 O2 (g) → 7 CO2 (g) + 3 H2 O(l)
Calcolare la variazione della capacità termica tra 298 K e 313 K, assumendo che le capacità termiche molari dei
prodotti e dei reagenti siano costanti nell’intervallo di temperatura tra 290 K e 320 K e sapendo che ∆H r (298K)
= -3250.1 kJ/mol e ∆Hr (313K) = -3248.2 kJ/mol.
Soluzione
La dipendenza dalla temperatura dell’entalpia di una reazione è stabilita dalla legge di Kirchoff:
Z T2
∆Hr0 (T2 ) = ∆Hr0 (T1 ) +
∆CP,m (T )dT
(3)
T1
L’esercizio indica che le capacità termiche di prodotti e reagenti sono costanti nell’intervallo di temperatura
considerato. L’equazione sopra puo’ quindi facilmente essere integrata
∆Hr0 (T2 ) = ∆Hr0 (T1 ) + ∆CP,m ∆T
da cui si ricava
∆CP,m =
∆Hr0 (T2 ) − ∆Hr0 (T1 )
(T2 − T1 )
Usando i dati riportati nel testo si ottiene
∆CP,m =
−3248.2 − (−3250.1) kJ/mol
= 127 J/(K · mol)
15K
6. Se il ∆Hf0 di CCl4 (l) è -135.4 kJ/mol e il ∆Hf0 di CCl4 (g) è di -102.9 kJ/mol, quanto è il calore richiesto
per vaporizzare due moli di CCl4 (l) a 298 K?
Soluzione
Il processo di vaporizzazione di CCl4 (l) è
6
CCl4 (l) → CCl4 (g)
L’entalpia di vaporizzazione si può ottenere dalle entalpie di formazione riportate nel testo
0
∆Hvap
= ∆Hf0 [CCl4 (g)] − ∆Hf0 [CCl4 (l)] = −102.9 kJ/mol − (−135.4 kJ/mol) = 32.5 kJ/mol
da cui, il calore di vaporizzazione di due moli di CCl4 (l) è
0
qvap = n · ∆Hvap
= 2 mol · 32.5 kJ/mol = 65.0 kJ/mol
7. Il seguente differenziale
nRT
dV
V
è esatto o inesatto? Considerare CV una semplice funzione di T .
Che cosa si può dire di x/T ? C’è una funzione di stato termodinamica che si comporta in questo modo?
dx = CV dT +
Soluzione
L’equazione dx = CV dT + nRT
V dV indica che x è funzione di T e V , x = x(T, V ). Possiamo anche esprimere dx
scrivendone la sua derivata totale
∂x
∂x
dT +
dV
dx =
∂T V
∂V T
Eguagliando le due equazioni si ottiene
e
∂x
∂T
∂x
∂V
= CV
V
=
T
nRT
V
Perche’ il differenziale in esame sia esatto devono essere uguali tra loro le derivate parziali seconde miste. Cioè:
∂
∂
∂x
∂x
=
∂V T ∂T V
∂T V ∂V T
In questo caso si ottiene:
∂
∂V
T
∂x
∂T
=0
V
∂
∂T
V
∂x
∂V
=
T
nR
V
perchè CV , come indicato nel testo dell’esercizio, dipende solo da T . Quindi il differenziale in esame non è
esatto.
Se invece si considera x/T si ottiene d Tx = CTV dT + nR
V dV da cui si ricava che
x
x
∂T
∂T
∂
∂
=0
=0
∂V T ∂T V
∂T V ∂V T
il differenziale, in questo caso, è esatto.
La funzione di stato che si comporta in questo modo è l’entropia, dove x = qrev .
8. Dite tutto quello che sapete sul secondo principio della termodinamica.
Soluzione
La risposta all’esercizio doveva prevedere come minimo la definizione dell’entropia e la discussione della disuguaglianza di Clausius per processi reversibili e irreversibili, le relazioni di spontaneità di un processo per un
7
sistema isolato. Enunciati di Clausius e Kelvin.
9. Il calore di transizione dalla fase α alla fase β per il ferro è, alla temperatura di transizione, pari a 1.715
kJ/(g·atomo). La variazione di entropia relativa alla trasformazione è di 1.66 J/(K·g·atomo). Quale è la temperatura di transizione?
Soluzione
Dalla definizione di entropia sappiamo che
qrev
T
corrisponde al calore di transizione e T alla temperatura di transizione, quindi si ottiene
∆S =
In questo caso, qrev
facilmente che
Tα/β =
qα/β
1715 J/(g · atomo)
=
= 1003 K
∆Sα/β
1.660 J/(g · atomo)
10. Ricavare la relazione di Maxwell corrispondente a dU = T dS − P dV .
Soluzione
Data l’equazione dU = T dS − P dV che indica come S e V siano le variabili naturali dell’energia interna,
U = U (S, V ), possiamo anche esprimere dU scrivendo la derivata totale di U
∂U
∂U
dS +
dV
dU =
∂S V
∂V S
Eguagliando le due equazioni si ottiene
e
∂U
∂S
∂U
∂V
=T
V
= −P
S
Sfruttando il fatto che le derivate parziali seconde miste sono uguali
∂
∂U
∂U
∂
=
∂V S ∂S V
∂S V ∂V S
si ricava
∂T
∂V
=−
S
∂P
∂S
V
Parte facoltativa
11. Nell’ipotesi di comportamento tipo van der Waals, quale membro i ciascuna delle seguenti coppie è più
probabile che devii dal comportamento ideale?
a) H2 rispetto a monossido di carbonio
b) Azoto rispetto a O2
8
Spiegate le vostre scelte.
Aiutatevi tenendo conto che le costanti di van der Waals sono:
gas
H2
N2
O2
CO
a (dm6 ·bar·mol−2 )
0.244
1.390
1.360
1.485
b (dm3 ·mol−1 )
2.661
3.913
3.183
3.985
Soluzione
a) Il monossido di carbonio è una molecola più pesante, voluminosa, leggermente dipolare e più polarizzabile
dell’idrogeno questo si manifesta nel valore decisamante più grande delle costanti a e b. In particolare, la
costante a è molto più grande e il CO risentirà di forze di attrazione intermolecolari maggiori deviando
dall’idealità più facilmente dell’idrogeno.
b) Azoto e ossigeno hanno valori delle costanti di van der Waals molto simili quindi tenderanno a comportarsi
in modo simile. Però l’azoto ha valori di a e b leggermente maggiori e avrà più tendenza a deviare
dall’idealità rispetto all’ossigeno.
12. Il coefficiente di espansione termica, α, di una sostanza è definito come
1 ∂V
α=
V ∂T P
Un liquido che si trova alla temperatuta T1 e volume V1 viene riscaldato da T1 a T2 a pressione costante.
Trovare un’espressione per V2 considerando α indipendente dalla temperatura
Soluzione
Dato che si ha
α=
1
V
∂V
∂T
=
P
1
V
dV
dT
per variazioni infinitesime a pressione costante si ottiene
1
dV = αdT
V
Integrando l’equazione sopra e considerando α indipendente dalla temperatura si ricava
1
dV = αdT
V
da cui
ln
V2
= α(T2 − T1 )
V1
e
V2 = V1 eα(T2 −T1 )
13. Si dispongano le seguenti reazioni secondo valori crescenti di ∆Sr0 (senza consultare fonti di riferimento)
(a) 2 H2 (g) + O2 (g) → H2 O(l)
(b) NH3 (g) + HCl(g) → NH4 Cl(s)
9
(c) K(s) + O2 (g) → KO2 (s)
(d) N2 (g) + 3 H2 (g) → 2 NH3 (g)
Soluzione
Nell’ordinare le reazioni in esame, si può tenere conto del fatto che le entropie di solidi e liquidi sono molto
più piccole di quelle dei gas. Possiamo cosı̀ trascurare il contributo dato a ∆S r0 da solidi e liquidi e considerare
solo i prodotti e i reagenti che si trovano in forma gassosa. Come parametro per la variazione di entropia della
reazione si può usare la differenza di moli, tra prodotti e reagenti gassosi. Quindi si ha
a. ∆n = −3
b. ∆n = −2
c. ∆n = −1
L’ordine corretto delle reazioni è pertanto: c > b ≈ d > a
10
d. ∆n = −2
CORSO DI LAUREA IN CHIMICA - ANNO ACCADEMICO 2005-06
ESAME DI CHIMICA FISICA A
March 31, 2006
COMPITO I
Regole per lo svolgimento dell’esame
1) barrare gli esercizi che si sono svolti;
2) scrivere qui sotto in quale pagina si trova l’esercizio svolto;
3) separare nettamente, con una riga, la fine di un esercizio dall’inizio di un altro;
4) mettere nome e cognome su ogni foglio;
5) sottolineare il risultato finale.
Cognome: ..................................................
Nome: ........................................
Data di nascita: ........................................
Firma: ........................................
N. di Matricola: ...........................
Parte obbligatoria
1. Enunciare il primo principio della termodinamica e discuterlo.
2. Per la reazione NH4 NO3 (s) → N2 O(g) + 2 H2 O(g), ∆H = -31.0 kJ a 400◦ C e 3.00 atm di pressione totale.
Calcolate il ∆U del processo. (Assumere che i gas si comportino in modo ideale)
3. Discutete il significato fisico dell’energia libera di Gibbs per un processo spontaneo.
4. Data la relazione
∂H
∂P
=V −T
T
∂V
∂T
P
calcolare il suo valore nel caso di un gas ideale. Come interpretate il risultato ottenuto?.
5. Calcolate la variazione di energia di Gibbs relativa alla dissociazione di 1 mol di N 2 O4 (g) in 2 mol di NO2 (g)
a 298 K. La variazione di entropia molare è 4.8 J/(K mol). (Usare: ∆H f0 (298K)[NO2 (g)] = 33.2 kJ/mol e
∆Hf0 (298K)[N2 O4 (g)] = 9.2 kJ/mol).
6. Quanto valgono q, w, ∆U e T (a) per un’espansione adiabatica reversibile e (b) per un’espansione isoterma
reversibile di un gas ideale? Commentare i risultati.
7. L’entalpia di combustione a 25◦ C di etanolo liquido, C2 H5 OH, idrogeno gassoso e grafite, per formare CO2 (g)
e H2 O(l), sono rispettivamente: 1366.9 kJ/mol, 285.8 kJ/mol e 393.5 kJ/mol. Scrivere le reazioni corrispondenti
alla combustione dei tre composti (es. H2 (g) + 21 O2 (g) → H2 O(l)) e poi la reazione di formazione dell’etanolo
liquido, infine combinarle e calcolare l’entalpia di formazione ∆Hf0 per l’etanolo liquido a 298.15 K.
8. A 0◦ C il ghiaccio ha una densità di 0.9170 g/cm3 ed un entropia molare di 37.95 J · K −1 · mol−1 . A questa
temperatura l’acqua liquida ha una densità di 0.9998 g/cm3 ed una entropia molare di 59.94 J · K −1 · mol−1 .
Calcolate (a) la variazione di entropia; (b) la variazione di entalpia; e (c) la variazione di energia interna per la
11
conversione di 1 mole di ghiaccio in acqua liquida alla temperatura di fusione normale e a pressione ambiente.
(PMol(H2 O) = 18.015 g/mol).
9. Ricavare la relazione di Maxwell che si ottiene partendo dalla definizione di G = A + P V .
10. Usando il risultato dell’esercizio precedente risolvete il seguente problema. Sia data una mole di gas Cl 2 con
un’entropia di 233 J/K che occupa un volume di 24.46 dm3 a 298 K. Fino a quale pressione sarebbe necessario
portare il gas per diminuire la sua entropia del 10% a temperatura costante? (Assumere che il gas si comporti
in modo ideale).
Parte facoltativa
11. Suggerite la ragione principale del perchè aumenta l’entropia in una reazione quale:
Br2 (l) + Cl2 (g) → 2 BrCl(g)
12. La fusione del cloruro di sodio richiede 30.3 kJ/mol, l’aumento di entropia è di 28.2 J · K −1 · mol−1 .
Calcolate da questi dati la temperatura di fusione.
13. Sapendo che
α2 T V
κ
1 ∂V
κ=−
V ∂P T
1 ∂V
α=
V ∂T P
CP − C V =
e
calcolare CP − CV per un gas ideale.
12
CORSO DI LAUREA IN CHIMICA - ANNO ACCADEMICO 2005-06
ESAME DI CHIMICA FISICA A
March 31, 2006
COMPITO II
Regole per lo svolgimento dell’esame
1) barrare gli esercizi che si sono svolti;
2) scrivere qui sotto in quale pagina si trova l’esercizio svolto;
3) separare nettamente, con una riga, la fine di un esercizio dall’inizio di un altro;
4) mettere nome e cognome su ogni foglio;
5) sottolineare il risultato finale.
Cognome: ..................................................
Nome: ........................................
Data di nascita: ........................................
Firma: ........................................
N. di Matricola: ...........................
Parte obbligatoria
1. Enunciare il terzo principio della termodinamica e discuterlo.
2. A 0◦ C il ghiaccio ha una densità di 0.9170 g/cm3 ed un entropia molare di 37.95 J · K −1 · mol−1 . A questa
temperatura l’acqua liquida ha una densità di 0.9998 g/cm3 ed una entropia molare di 59.94 J · K −1 · mol−1 .
Calcolate (a) la variazione di entropia molare; (b) la variazione di entalpia; e (c) la variazione di energia interna
per la conversione di 1 mole di ghiaccio in acqua liquida alla temperatura di fusione normale e a pressione
ambiente. (PMol(H2 O) = 18.015 g/mol)
3. La fusione del cloruro di potassio richiede 27.6 kJ/mol, l’aumento di entropia è di 26.5 J · K −1 · mol−1 .
Calcolate da questi dati la temperatura di fusione.
4. Quanto valgono q, w, ∆U e T (a) per un’espansione adiabatica reversibile e (b) per un’espansione isoterma
reversibile di un gas ideale? Commentare i risultati.
5. Discutete il significato fisico dell’energia libera di Gibbs per un processo spontaneo.
6. Calcolate la variazione di energia di Gibbs relativa alla dissociazione di 1 mol di N 2 O4 (g) in 2 mol di NO2 (g)
a 298 K. La variazione di entropia molare è 4.8 J/(K mol). (Usare: ∆H f0 (298K)[NO2 (g)] = 33.2 kJ/mol e
∆Hf0 (298K)[N2 O4 (g)] = 9.2 kJ/mol)
7. Data la relazione
∂U
∂V
=P −T
T
∂P
∂T
V
calcolare il suo valore nel caso di un gas ideale. Come interpretate il risultato ottenuto?
8. L’entalpia di combustione a 25◦ C di etanolo liquido, C2 H5 OH, idrogeno gassoso e grafite, per formare CO2 (g)
e H2 O(l), sono rispettivamente: 1366.9 kJ/mol, 285.8 kJ/mol e 393.5 kJ/mol. Scrivere le reazioni corrispondenti
13
alla combustione dei tre composti (es. H2 (g) + 21 O2 (g) → H2 O(l)) e poi la reazione di formazione dell’etanolo
liquido, infine combinarle e calcolare l’entalpia di formazione ∆Hf0 per l’etanolo liquido a 298.15 K.
9. Ricavare la relazione di Maxwell che si ottiene partendo dalla definizione di A = U − T S.
10. Usando il risultato dell’esercizio precedente risolvete il seguente problema. Sia data una mole di gas Cl 2 con
un’entropia di 233 J/K a 1.00 atm e 298 K. A quale volume sarebbe necessario espandere il gas per aumentare
la sua entropia del 10% a temperatura costante? (Assumere che il gas si comporti in modo ideale).
Parte facoltativa
11. Per la reazione NH4 NO3 (s) → N2 O(g) + 2 H2 O(g), ∆H = -31.0 kJ a 400◦ C e 3.00 atm di pressione totale.
Calcolate il ∆U del processo.
12. Sapendo che
α2 T V
κ
1 ∂V
κ=−
V ∂P T
1 ∂V
α=
V ∂T P
CP − C V =
e
calcolare CP − CV per un gas ideale.
13. Suggerite la ragione principale del perchè diminuisce l’entropia in una reazione quale:
2 H2 (g) + O2 (g) → H2 O(l)
14
CORSO DI LAUREA IN CHIMICA - ANNO ACCADEMICO 2005-06
CORREZIONE DELL’ESAME DI CHIMICA FISICA A
March 31, 2006
COMPITO I
Parte obbligatoria
1. Enunciare il secondo principio della termodinamica e discuterlo.
Soluzione
La risposta all’esercizio doveva prevedere come minimo la definizione dell’entropia e la discussione della disuguaglianza di Clausius per processi reversibili e irreversibili, le relazioni di spontaneità di un processo per un
sistema isolato. Enunciati di Clausius e Kelvin.
2. Per la reazione NH4 NO3 (s) → N2 O(g) + 2 H2 O(g), ∆H = -31.0 kJ a 400◦ C e 3.00 atm di pressione totale.
Calcolate il ∆U del processo. (Assumere che i gas si comportino in modo ideale)
Soluzione
Per poter calcolare ∆U si sfrutta la relazione H = U + P V da cui a pressione costante si ottiene
∆U = ∆H − P ∆V
∆V non è noto, ma dato che nella reazione un solido si trasforma in due prodotti gassosi, si può assumere che
tutta la variazione di volume sia dovuta alla formazione di N2 O(g) e H2 O(g). Se i gas si comportano in modo
ideale allora dall’equazione di stato dei gas ideali si ricava
∆V =
∆n RT
P
cioè la variazione di volume è associata ad una variazione del numero di moli di gas che in questo caso coincide
con il numero di moli di gas che si formano. Quindi
∆U = ∆H − P ∆V = ∆H − P
∆n RT
= ∆H − ∆n RT
P
sostituendo i dati forniti nel testo si ottiene infine
∆U = −31.0kJ · −3 mol · 8.3145 J · K −1 mol−1 · 673.15 K = −47.8 kJ
3. Discutete il significato fisico dell’energia libera di Gibbs per un processo spontaneo.
Soluzione
Vedere paragrafo 22.2 del McQuarrie.
15
4. Data la relazione
∂H
∂P
=V −T
T
∂V
∂T
P
calcolare il suo valore nel caso di un gas ideale. Come interpretate il risultato ottenuto?.
Soluzione
Data l’equazione di stato di un gas ideale l’ultimo termine a destra diventa
∂H
nR
=V −T ·
∂P T
P
Esprimendo poi il volume in termini di P e T si arriva a
∂H
nRT
nRT
=
−
=0
∂P T
P
P
Il risultato ottenuto dimostra come per un gas ideale l’entalpia non dipenda dalla pressione.
5. Calcolate la variazione di energia di Gibbs relativa alla dissociazione di 1 mol di N 2 O4 (g) in 2 mol di NO2 (g)
a 298 K. La variazione di entropia molare è 4.8 J/(K mol). (Usare: ∆H f0 (298K)[NO2 (g)] = 33.2 kJ/mol e
∆Hf0 (298K)[N2 O4 (g)] = 9.2 kJ/mol).
Soluzione
Occorre prima calcolare il ∆Hr0 della reazione
N2 O4 (g) → 2 NO2 (g)
dai dati a disposizione si ha.
∆Hr0 = 2 · ∆Hf0 [N O2 (g)] − ∆Hf0 [N2 O4 (g)] = 2 · 33.2 kJ/mol − 9.2 kJ/mol = 57.2 kJ/mol
Data la variazione di entropia, si ricava immediatamente
∆G0r = ∆Hr0 − T ∆Sr0 = 57.2 kJ/mol − 298 K · 4.8 J · K −1 · mol−1 = 55.8 kJ/mol
6. Quanto valgono q, w, ∆U e T (a) per un’espansione adiabatica reversibile e (b) per un’espansione isoterma
reversibile di un gas ideale? Commentare i risultati.
Soluzione
(a) Per un’espansione reversibile adiabatica non c’è scambio di calore quindi q = 0 . Per cui vale:
∆U = w = CV ∆T .
∆T si può ottenere tenendo conto che dU = δw, che per si può anche scrivere come C V dT = −P dV . Per
un gas ideale P = RT
V e si ha
nRT
dV
CV dT = −
V
da cui
dT
nR dV
=−
T
CV V
16
Integrando tra (Ti , Vi ) e (Tf , Vf ) e tenendo conto che CRV non dipende dal volume, si ottiene
Z Tf
Z Vf
R
dV
dT
=−
T
C
V
V
Ti
Vi
R
Vf
Tf
=−
ln
= ln
ln
Ti
CV
Vi
da cui, ponendo
CV
R
Vi
Vf
CR
V
= γ, si ricava
Tf
=
Ti
Vi
Vf
quindi
Tf =
da cui
∆T =
Vi
Vf
Vi
Vf
γ1
γ1
γ1
Ti
−1
Ti
La dipendenza dalla temperatura di una espansione adiabatica reversibile di un gas ideale poteva essere
espressa indifferentemente attraverso una delle relazioni scritte sopra.
(b) Per un’espansione reversibile isoterma non c’è variazione di temperatura quindi ∆T = 0 . Inoltre,
l’energia interna di un gas ideale dipende solo dalla temperatura per cui ∆U = 0 . Allora, dal primo
principio: q = −w .
Tenendo conto che δw = −P dV e che per un gas ideale P =
δw = −
RT
V
, si ha
nRT
dV
V
che integrata diventa
w = −nRT ln
Vf
Vi
Commento:
(a) Il lavoro compiuto dal gas che si espande comporta un decremento di energia interna, ciò provoca una
diminuzione della temperatura e il gas si raffredda.
(b) Il lavoro è negativo perchè è il gas che compie lavoro, mentre q è positivo perchè è entrata energia come
calore per mantenere la temperatura constante, dato che il sistema ha usato la sua energia per compiere
il lavoro.
7. L’entalpia di combustione a 25◦ C di etanolo liquido, C2 H5 OH, idrogeno gassoso e grafite, per formare CO2 (g)
e H2 O(l), sono rispettivamente: 1366.9 kJ/mol, 285.8 kJ/mol e 393.5 kJ/mol. Scrivere le reazioni corrispondenti
alla combustione dei tre composti (es. H2 (g) + 21 O2 (g) → H2 O(l)) e poi la reazione di formazione dell’etanolo
liquido, infine combinarle e calcolare l’entalpia di formazione ∆Hf0 per l’etanolo liquido a 298.15 K.
Soluzione
Le reazioni in gioco sono
(1)
(2)
(3)
C2 H5 OH(l) + 3 O2 (g) → 2 CO2 (g) + 3 H2 O(l)
H2 (g) + 12 O2 (g) → H2 O(l)
C(s) + O2 (g) → CO2 (g)
∆Hc0 = 1366.9 kJ/mol
∆Hc0 = 285.8 kJ/mol
∆Hc0 = 393.5 kJ/mol
(4)
2 C(s) + 3 H2 (g) + 12 O2 (g) → C2 H5 OH(l)
∆Hf0 = ?
17
Per calcolare ∆Hf0 (298.15 K) dell’etanolo liquido si può usare la legge di Hess e combinare le reazioni a disposizione (1-3) per ottenere la (4). In particolare, la (4) si può ottenere invertendo la reazione (1) e sommando ad
essa le reazioni (2) e (3), moltiplicate rispettivamente per 3 e 2.
L’entalpia di formazione dell’etanolo liquido a 298.15 K, risulta quindi essere
∆Hf0 [C2 H5 OH(l)] = −∆Hc0 (1) + 3 · ∆Hc0 (2) + 2 · ∆Hc0 (3)
Sostituendo i dati numerici si ottiene
∆Hf0 [C2 H5 OH(l)] = −1366.9 + 3 · 285.8 + 2 · 393.5 = 277.5 kJ/mol
8. A 0◦ C il ghiaccio ha una densità di 0.9170 g/cm3 ed un entropia molare di 37.95 J · K −1 · mol−1 . A questa
temperatura l’acqua liquida ha una densità di 0.9998 g/cm3 ed una entropia molare di 59.94 J · K −1 · mol−1 .
Calcolate (a) la variazione di entropia; (b) la variazione di entalpia; e (c) la variazione di energia interna per la
conversione di 1 mole di ghiaccio in acqua liquida alla temperatura di fusione normale e a pressione ambiente.
(PMol(H2 O) = 18.015 g/mol).
Soluzione
(a)
∆Sf us = S(l) − S(s) = 59.94 − 37.95 = 21.99 J · K −1 · mol−1
(b) Dato che una transizione di fase è un processo di equilibrio allora ∆Gf us = 0 quindi
∆Hf us = Tf us · ∆Sf us = 273.15 K · 21.99J · K −1 · mol−1 = 6006.6 J/mol
(c) La variazione di energia interna si ricava da ∆U = ∆H − P ∆V . La variazione di volume si ottiene dai
dati di densità di acqua e ghiaccio
∆Vm = V (l) − V (s) =
P M ol P M ol
18.015 g/mol
18.015 g/mol
−
=
−
= −1.63 · 10−6 m3 /mol
ρ(l)
ρ(s)
0.9998 g/cm3 0.9170 g/cm3
da cui
∆Uf us = 6006.6 J/mol − 1.00 atm · 1.01325 · 105 P a/atm · (−1.63 · 10−6 m3 /mol) = 6008.2 J/mol
9. Ricavare la relazione di Maxwell che si ottiene partendo dalla definizione di G = A + P V .
Soluzione
Data la definizione G = A + P V si può anche scrivere G = U − T S + P V , che in forma differenziale diventa
dG = dU − T dS − SdT + P dV + V dP . Dal primo principio si ha: dU = T dS + P dV che sostituita nella relazione
precedente dà:
dG = T dS + P dV − T dS − SdT + P dV + V dP
dG = −SdT + V dP
che indica come T e P siano le variabili naturali dell’energia interna, G = G(T, P ). Usando questo risultato,
possiamo anche esprimere dG attraverso la sua derivata totale
∂G
∂G
dT +
dP
dG =
∂T P
∂P T
18
Eguagliando le due equazioni si ottiene
e
∂G
∂T
∂G
∂P
= −S
P
=V
T
Sfruttando il fatto che le derivate parziali seconde miste sono uguali
∂
∂
∂G
∂G
=
∂P T ∂T P
∂T P ∂P T
si ricava
−
∂S
∂P
=
T
∂V
∂T
P
10. Sia data una mole di gas Cl2 con un’entropia di 233 J/K che occupa un volume di 24.46 dm3 a 298 K.
Fino a quale pressione sarebbe necessario portare il gas per diminuire la sua entropia del 10% a temperatura
costante? (Fate riferimento all’esito dell’esercizio precedente)(Assumere che il gas si comporti in modo ideale).
Soluzione
Sulla base del risultato dell’esercizio precedente
∂V
∂S
=
−
∂P T
∂T P
usando l’equazione di stato dei gas ideali, si ottiene
nR
∂S
=
−
∂P T
P
da cui, a temperatura costante,
dS = −
che in forma integrata diventa
∆S = −nR
Z
Pf
Pi
nR
dP
P
Pf
dP
= −nR · ln
P
Pi
L’esercizio richiede di calcolare la pressione finale rispetto ad una variazione di entropia per cui
−
∆S
Pf
= ln
nR
Pi
e
∆S
Pf = Pi · e− nR
Dai dati dell’esercizio si ricava
Pi =
nRT
0.0821 atm · dm3 · K −1 · mol−1 · 298 K
=
= 1.00 atm
V
24.46 dm3
data una diminuzione di entropia del 10% si ricava ∆S = −23.3 J · K −1 · mol−1 . Quindi
−23.3 J·K −1 ·mol−1
J·K −1 ·mol−1
∆S
Pf = Pi · e− nR = 1.00 atm · e− 8.3145
19
= 16.5 atm
Parte facoltativa
11. Suggerite la ragione principale del perchè aumenta l’entropia in una reazione quale:
Br2 (l) + Cl2 (g) → 2 BrCl(g)
Soluzione
Data l’interpretazione molecolare dell’entropia, ne consegue che le entropie di solidi e liquidi sono molto più
piccole di quelle dei gas. È possibile quindi trascurare il contributo dato a ∆Sr0 da solidi e liquidi e considerare
solo i prodotti e i reagenti che si trovano in forma gassosa. Come parametro per la variazione di entropia della
reazione si può usare la differenza di moli tra prodotti e reagenti gassosi.
Quindi, nel caso della reazione in esame, dato che ∆n = 1 si ha un aumento di entropia.
12. La fusione del cloruro di sodio richiede 30.3 kJ/mol, l’aumento di entropia è di 28.2 J · K −1 · mol−1 .
Calcolate da questi dati la temperatura di fusione.
Soluzione
Una transione di fase è un processo di equilibrio quindi ∆Gf us,m = 0, ma ∆Gf us,m = ∆Hf us,m − T · ∆Sf us,m
e quindi, alla temperatura di fusione, si ha:
Tf us =
∆Hf us,m
30300 J/mol
=
= 1070 K
∆Sf us,m
28.2 J/(K · mol)
13. Sapendo che
α2 T V
κ
1 ∂V
κ=−
V ∂P T
1 ∂V
α=
V ∂T P
CP − C V =
e
calcolare CP − CV per un gas ideale.
Soluzione
κ e α dipendono, rispettivamente, dalle derivate parziali del volume rispetto a P a temperatura costante e
rispetto a T a pressione costante. Nel caso di un gas ideale (V = nRT
P ) esplicitando le derivate parziali si ottiene
1 nRT
P nRT
1
1 ∂V
=
=
=
κ=−
2
2
V ∂P T
V P
nRT P
P
e
α=
1
V
∂V
∂T
=
P
1 nR
P nR
1
=
=
V P
nRT P
T
usando questi risultati si ha
α2 T V
1
PV
= 2 · TV · P =
κ
T
T
data l’equazione di stato di un gas ideale si ricava infine
CP − C V =
CP − CV = nR
20
CORSO DI LAUREA IN CHIMICA - ANNO ACCADEMICO 2005-06
CORREZIONE DELL’ESAME DI CHIMICA FISICA A
March 31, 2006
COMPITO II
Parte obbligatoria
1. Enunciare il terzo principio della termodinamica e discuterlo.
Soluzione
La risposta doveva come minimo prevedere l’enunciato del terzo principio che stabilisce che a 0 K l’entropia di
una sostanza pura nel proprio stato più stabile è nulla. Eventualmente, si potevano dare altri enunciati come
quello di Nerst o quello dell’impossibilità di raggiungere lo zero assoluto con un numero finito di operazioni.
Il commento del terzo principio deve almeno comprendere il fatto che l’entropia di una sostanza è una quantità
positiva e che è possibile definire un’entropia assoluta. Eventualmente, si poteva riportare la relazione che
esprime la dipendenza dell’entropia dalla temperatura.
2. A 0◦ C il ghiaccio ha una densità di 0.9170 g/cm3 ed un entropia molare di 37.95 J · K −1 · mol−1 . A questa
temperatura l’acqua liquida ha una densità ha una densità di 0.9998 g/cm3 ed una entropia molare di 59.94
J · K −1 · mol−1 . Calcolate (a) la variazione di entropia molare; (b) la variazione di entalpia; e (c) la variazione
di energia interna per la conversione di 1 mole di ghiaccio in acqua liquida alla temperatura di fusione normale.
(PMol(H2 O) = 18.015 g/mol)
Soluzione
Vedere esercizio 8 del Compito I.
3. La fusione del cloruro di potassio richiede 27.6 kJ/mol, l’aumento di entropia è di 26.5 J · K −1 · mol−1 .
Calcolate da questi dati la temperatura di fusione.
Soluzione
Una transione di fase è un processo di equilibrio quindi ∆Gf us,m = 0, ma ∆Gf us,m = ∆Hf us,m − T · ∆Sf us,m
e quindi, alla temperatura di fusione, si ha:
Tf us =
∆Hf us,m
27600 J/mol
=
= 1042 K
∆Sf us,m
26.5 J/(K · mol)
4. Quanto valgono q, w, ∆U e T (a) per un’espansione adiabatica reversibile e (b) per un’espansione isoterma
reversibile di un gas ideale? Commentare i risultati.
Soluzione
21
Vedere esercizio 6 del Compito I.
5. Discutete il significato fisico dell’energia libera di Gibbs per un processo spontaneo.
Soluzione
Vedere paragrafo 22.2 del McQuarrie.
6. Calcolate la variazione di energia di Gibbs relativa alla dissociazione di 1 mol di N 2 O4 (g) in 2 mol di NO2 (g)
in condizioni standard. La variazione di entropia molare è 4.8 J/(K mol). (Usare: ∆H f0 (298K)[NO2 (g)] = 33.2
kJ/mol e ∆Hf0 (298K)[N2 O4 (g)] = 9.2/mol)
Soluzione
Vedere esercizio 5 del Compito I.
7. Data la relazione
∂U
∂V
=P −T
T
∂P
∂T
V
calcolare il suo valore nel caso di un gas ideale. Come interpretate il risultato ottenuto?
Soluzione
Data l’equazione di stato di un gas ideale l’ultimo termine a destra diventa
∂U
nR
=P −T ·
∂V T
V
Esprimendo poi la pressione in termini di V e T si arriva a
nRT
nRT
∂U
=
−
=0
∂V T
V
V
Il risultato ottenuto dimostra come per un gas ideale l’energia interna non dipenda dal volume.
8. L’entalpia di combustione a 25◦ C di etanolo liquido, C2 H5 OH, idrogeno gassoso e grafite, per formare CO2 (g)
e H2 O(l), sono rispettivamente: 1366.9 kJ/mol, 285.8 kJ/mol e 393.5 kJ/mol. Scrivere le reazioni corrispondenti
alla combustione dei tre composti (es. H2 (g) + 21 O2 (g) → H2 O(l)) e poi la reazione di formazione dell’etanolo
liquido, infine combinarle e calcolare l’entalpia di formazione ∆Hf0 per l’etanolo liquido a 298.15 K.
Soluzione
Vedere esercizio 7 del Compito I.
22
9. Ricavare la relazione di Maxwell che si ottiene partendo dalla definizione di A = U − T S.
Soluzione
Dalla definizione A = U − T S si può in forma differenziale che dA = dU − T dS − SdT . Dal primo principio si
ha: dU = T dS − P dV , che sostituita nella relazione precedente dà:
dA = T dS − P dV − T dS − SdT
dA = −SdT − P dV
che indica come T e V siano le variabili naturali dell’energia interna, A = A(T, V ). Usando questo risultato,
possiamo anche esprimere dA attraverso la sua derivata totale
∂A
∂A
dT +
dV
dA =
∂T V
∂V T
Eguagliando le due equazioni si ottiene
e
∂A
∂T
∂A
∂V
= −S
V
= −P
T
Sfruttando il fatto che le derivate parziali seconde miste sono uguali
∂A
∂A
∂
∂
=
∂V T ∂T V
∂T V ∂V T
si ricava la relazione di Maxwell richiesta
∂S
∂V
=
T
∂P
∂T
V
10. Sia data una mole di gas Cl2 con un’entropia di 233 J/K a 1.00 atm e 298 K. A quale volume sarebbe
necessario espandere il gas per aumentare la sua entropia del 10% a temperatura costante? (Fate riferimento
all’esito dell’esercizio precedente) (Assumere che il gas si comporti in modo ideale).
Soluzione
Sulla base del risultato dell’esercizio precedente
∂P
∂S
=
∂V T
∂T V
usando l’equazione di stato dei gas ideali, si ottiene
nR
∂S
=
∂V T
V
da cui, a temperatura costante,
dS =
che in forma integrata diventa
∆S = nR
Z
Vf
Vi
nR
dV
V
Vf
dV
= nR · ln
V
Vi
23
L’esercizio richiede di calcolare il volume finale rispetto ad una variazione di entropia per cui
∆S
Vf
= ln
nR
Vi
e
∆S
Vf = Vi · e nR
Dai dati dell’esercizio si ricava
Vi =
nRT
0.0821 atm · dm3 · K −1 · mol−1 · 298 K
=
= 24.46 dm3
P
1.00 atm
data un aumento di entropia del 10% si ricava ∆S = 23.3 J · K −1 · mol−1 . Quindi
∆S
23.3 J·K −1 ·mol−1
J·K −1 ·mol−1
Vf = Vi · e nR = 24.46 dm3 · e 8.3145
= 403.3 dm3
Parte facoltativa
11. Per la reazione NH4 NO3 (s) → N2 O(g) + 2 H2 O(g) ∆H = -31.0 kJ a 400◦ C e 3.00 atm di pressione totale.
Calcolate il ∆U del processo.
Soluzione
Vedere esercizio 2 del Compito I.
12. Sapendo che
α2 T V
κ
1 ∂V
κ=−
V ∂P T
1 ∂V
α=
V ∂T P
CP − C V =
e
calcolare CP − CV per un gas ideale.
Soluzione
Vedere esercizio 13 del Compito I.
13. Suggerite la ragione principale del perchè diminuisce l’entropia in una reazione quale:
2 H2 (g) + O2 (g) → H2 O(l)
Soluzione
Data l’interpretazione molecolare dell’entropia, ne consegue che le entropie di solidi e liquidi sono molto più
piccole di quelle dei gas. È possibile quindi trascurare il contributo dato a ∆Sr0 da solidi e liquidi e considerare
solo i prodotti e i reagenti che si trovano in forma gassosa. Come parametro per la variazione di entropia della
reazione si può usare la differenza di moli tra prodotti e reagenti gassosi.
Quindi, nel caso della reazione in esame, dato che ∆n = −3 si ha un diminuzione di entropia.
24
CORSO DI LAUREA IN CHIMICA - ANNO ACCADEMICO 2005-06
ESAME DI CHIMICA FISICA A
April 21, 2006
COMPITO I
Regole per lo svolgimento dell’esame
1) barrare gli esercizi che si sono svolti;
2) scrivere qui sotto in quale pagina si trova l’esercizio svolto;
3) separare nettamente, con una riga, la fine di un esercizio dall’inizio
di un altro;
4) mettere nome e cognome su ogni foglio;
5) sottolineare il risultato finale.
Cognome: ..................................................
Nome: ........................................
Data di nascita: ........................................
Firma: ........................................
N. di Matricola: ...........................
Parte obbligatoria
1. Descriviamo l’azoto gassoso con l’equazione di van der Waals; le costanti sono a=1.3661 dm 6 · bar · mol−2 e
b=0.038577 dm3 · mol−1 ; determinare Tc , Pc e Vc . (Ricavare le formule e calcolare i valori numerici).
2. Sfruttando quanto ricavato nell’esercizio 1. dire se: (a) posso liquefare il gas se lavoro a T =1.1 ·T c ? (giustificare la risposta); (b) Se lavoro a T =110.2 K e V =0.10 dm3 mol−1 , quanto vale la pressione?
3. Siano dati due blocchi dello stesso materiale e della stessa massa a contatto tra di loro e isolati dall’intorno.
Sapendo che uno si trova ad una temperatura di 197◦C e l’altro ad una temperatura di 130◦C, determinare:
(a) la temperatura di equilibrio; (b) la variazione di entropia del corpo 1, del corpo 2 e la variazione totale; (c)
la variazione di energia interna totale. (Sia C̄V = 24.5 Jmol−1 K −1 non dipendente da T ).
4. Una mole di gas ideale monoatomico a V =20 l e T =278 K raddoppia il suo volume a T costante in modo
reversibile. (a) Quanto e’ il lavoro di espansione? (b) Il sistema assorbe o emette calore? (c) Quanto vale ∆H?
(d) Quanto vale ∆P ? (e) e ∆T ?
5. Lo stesso gas dell’esercizio precedente si espande adiabaticamente in modo reversibile: (a) quanto vale ∆T ?
(passaggi!). Ricordare che Cv = 3/2R e che ci si riferisce ad una mole.
6. Con riferimento all’esercizio precedente si calcolino le variazioni di P , U e H
7. Quanto vale ∆S: (a) nel caso dell’esercizio 4?; (b) e nel caso dell’esercizio 5?; (c) quanto vale ∆G nei due casi?
25
8. Le entalpie di combustione a 25◦ C di metanolo liquido, CH3 OH, idrogeno gassoso e grafite, per formare
CO2 (g) e H2 O(l), sono rispettivamente: 726.0 kJ/mol, 285.8 kJ/mol e 393.5 kJ/mol. Scrivere le reazioni corrispondenti alla combustione dei tre composti (es. H2 (g) + 12 O2 (g) → H2 O(l)) e poi la reazione di formazione
del metanolo liquido, infine combinarle e calcolare l’entalpia di formazione ∆Hf0 per il metanolo liquido a 298.15
K.
9. Dopo avere ricavato la relazione di Maxwell che si ottiene partendo dalla definizione di A(AR = U − T S),
determinare come varia S in funzione di V a T costante (scrivere la relazione nella forma ∆S = ...dV ).
10. Si consideri il gas di van der Waals con costanti date all’esercizio 1; sfruttando il risultato dell’esercizio
precedente, determinare la variazione di entropia per la trasformazione isoterma (T = 278 K) in cui il volume
viene raddoppiato da 20 a 40 l.
Parte facoltativa
11. Una mole di gas (ideale, monoatomico, a T1 = 278 K) viene scaldato a volume costante (20 l) fino a
T2 = 2T1 , di quanto aumenta U ?
12. Una mole di gas (ideale, monoatomico, a T1 = 278 K) viene scaldato a volume costante (20 l) fino a
T2 = 2T1 , di quanto aumentano P , H ed S?
13.
A = U − T S, derivare rispetto a V mantenendo T costante. Usare poi i risultati per
Data larelazione
∂A
∂S
e e ∂V
ottenuti in un esercizio precedente (relativo all’equazione di Maxwell ottenuta da A) per
∂V
T
T
∂U
=...
ottenere come varia U con il volume: ∂V
T
26
CORSO DI LAUREA IN CHIMICA - ANNO ACCADEMICO 2005-06
ESAME DI CHIMICA FISICA A
April 21, 2006
COMPITO II
Regole per lo svolgimento dell’esame
1) barrare gli esercizi che si sono svolti;
2) scrivere qui sotto in quale pagina si trova l’esercizio svolto;
3) separare nettamente, con una riga, la fine di un esercizio dall’inizio
di un altro;
4) mettere nome e cognome su ogni foglio;
5) sottolineare il risultato finale.
Cognome: ..................................................
Nome: ........................................
Data di nascita: ........................................
Firma: ........................................
N. di Matricola: ...........................
Parte obbligatoria
1. Siano dati due blocchi dello stesso materiale e della stessa massa a contatto tra di loro e isolati dall’intorno.
Sapendo che uno si trova ad una temperatura di 167◦C e l’altro ad una temperatura di 130◦C, determinare:
(a) la temperatura di equilibrio; (b) la variazione di entropia del corpo 1, del corpo 2 e la variazione totale; (c)
la variazione di energia interna totale. (Sia C̄V = 24.5 Jmol−1 K −1 non dipendente da T ).
2. Descriviamo l’azoto gassoso con l’equazione di van der Waals; le costanti sono a=1.3661 dm 6 · bar · mol−2 e
b=0.038577 dm3 · mol−1 ; determinare Tc , Pc e Vc . (Ricavare le formule e calcolare i valori numerici).
3. Sfruttando quanto ricavato nell’esercizio 2 dire se: (a) posso liquefare il gas se lavoro a T =0.9 ·T c ? (giustificare la risposta); (b) Se lavoro a T =100.2 K e V =0.10 dm3 mol−1 , quanto vale la pressione?
4. Una mole di gas ideale monoatomico a V =10 l e T =248 K raddoppia il suo volume a T costante in modo
reversibile. (a) Quanto e’ il lavoro di espansione? (b) Il sistema assorbe o emette calore? (c) Quanto vale ∆H?
(d) Quanto vale ∆P ? (e) e ∆T ?
5. Lo stesso gas dell’esercizio precedente si espande adiabaticamente in modo reversibile: (a) quanto vale ∆T ?
(passaggi!). Ricordare che Cv = 3/2R e che ci si riferisce ad una mole.
6. Con riferimento all’esercizio precedente si calcolino le variazioni di P , U e H
7. Quanto vale ∆S: (a) nel caso dell’esercizio 4; (b) e nel caso dell’esercizio 5; (c) quanto vale ∆G nei due casi?
27
8. Le entalpie di combustione a 25◦ C di metanolo liquido, CH3 OH, idrogeno gassoso e grafite, per formare
CO2 (g) e H2 O(l), sono rispettivamente: 746.0 kJ/mol, 275.8 kJ/mol e 393.5 kJ/mol. Scrivere le reazioni corrispondenti alla combustione dei tre composti (es. H2 (g) + 12 O2 (g) → H2 O(l)) e poi la reazione di formazione
del metanolo liquido, infine combinarle e calcolare l’entalpia di formazione ∆Hf0 per il metanolo liquido a 298.15
K.
9. Dopo avere ricavato la relazione di Maxwell che si ottiene partendo dalla definizione di A(AR = U − T S),
determinare come varia S in funzione di V a T costante (scrivere la relazione nella forma ∆S = ...dV ).
10. Si consideri il gas di van der Waals con costanti date all’esercizio 2; sfruttando il risultato dell’esercizio
precedente, determinare la variazione di entropia per la trasformazione isoterma (T = 248 K) in cui il volume
viene raddoppiato da 10 a 20 l.
Parte facoltativa
11. Una mole di gas (ideale, monoatomico, a T1 = 248 K) viene scaldato a volume costante (10 l) fino a
T2 = 2T1 , di quanto aumenta U ?
12. Una mole di gas (ideale, monoatomico, a T1 = 248 K) viene scaldato a volume costante (10 l) fino a
T2 = 2T1 , di quanto aumentano P , H ed S?
13.
A = U − T S, derivare rispetto a V mantenendo T costante. Usare poi i risultati per
Data larelazione
∂A
∂S
e e ∂V
ottenuti in un esercizio precedente (relativo all’equazione di Maxwell ottenuta da A) per
∂V
T
T
∂U
=...
ottenere come varia U con il volume: ∂V
T
28
CORSO DI LAUREA IN CHIMICA - ANNO ACCADEMICO 2005-06
CORREZIONE DELL’ESAME DI CHIMICA FISICA A
April 21, 2006
COMPITO I
Parte obbligatoria
1. Descriviamo l’azoto gassoso con l’equazione di van der Waals; le costanti sono a=1.3661 dm 6 · bar · mol−2 e
b=0.038577 dm3 · mol−1 ; determinare Tc , Pc e Vc . (Ricavare le formule e calcolare i valori numerici).
Soluzione
L’equazione di van der Waals puó essere scritta nella forma
(P +
a
)(V̄ − b) = RT
V̄ 2
o, in forma equivalente, come
RT 2
a
ab
)V̄ + V̄ −
= 0.
P
P
P
Quest’ultima e’ un’equazione cubica che possiede quindi tre radici. Al punto critico, queste tre radici coincidono
e quindi l’equazione puó essere scritta nella forma (V̄ − V̄c )3 = 0, ossia
V̄ 3 − (b +
V̄ 3 − 3V̄c V̄ 2 + 3V̄ c 2 V̄ − V̄ c 3 = 0.
Confrontando questa espressione con quella di partenza al punto critico, si hanno le tre equazioni seguenti
c
3V̄ c = b + RT
Pc ;
a
2
3V̄ c = Pc ;
V̄ c 3 = Pabc .
Confrontando la (2) e la (3) si ottiene:
(1)
(2)
(3)
V¯c = 3b
che sostituita nella (3) dá
Pc =
a
.
27b2
Sostituendo le espressioni ottenute per V¯c e Pc nella (1) si ha
Tc =
8a
.
27bR
Non resta quindi che sostituire i valori numerici delle costanti di van der Waals date dal problema per ottenere:
V̄ c =0.115731 dm3 mol−1
Pc =33.999 bar
Tc =126.195 K
29
Compito II, esercizio 2.
Descriviamo l’azoto gassoso con l’equazione di van der Waals; le costanti sono a=1.3661 dm 6 · bar · mol−2 e
b=0.038577 dm3 · mol−1 ; determinare Tc , Pc e Vc . (Ricavare le formule e calcolare i valori numerici).
Soluzione
idem.
2. Sfruttando quanto ricavato nell’esercizio 1 dire se: (a) posso liquefare il gas se lavoro a T =1.1 ·T c ? (giustificare la risposta); (b) Se lavoro a T =110.2 K e V =0.10 dm3 mol−1 , quanto vale la pressione?
Soluzione
(a) Non posso liquefare il gas perche’ Tc e’ la temperatura oltre la quale un gas non puó essere liquefatto,
indipendentemente dalla pressione.
(b) Le isoterme pressione-volume di un gas in un intorno della temperatura critica, si appiattiscono per T → T c
dando luogo a regioni orizzontali per T < Tc nelle quali il gas e il liquido coesistono in equilibrio tra loro.
Usando la legge di van der Waals esplicitata rispetto alla pressione
P =
a
RT
−
V̄ − b V̄ 2
e sostituendo i valori dati, si ha
P = 149.1718 bar − 136.6100 bar = 12.5618 bar = 1256.18 kP a .
Compito II, esercizio 3.
Sfruttando quanto ricavato nell’esercizio 2 dire se: (a) posso liquefare il gas se lavoro a T =0.9 ·T c ? (giustificare
la risposta); (b) Se lavoro a T =100.2 K e V =0.10 dm3 mol−1 , quanto vale la pressione?
Soluzione
(a) posso liquefare il gas;
(b) P = 135.635 bar − 136.610 bar = −0.975 bar = −97.47 kP a .
In questo caso van der Waals non é verificata, essendo P < 0.
3. Siano dati due blocchi dello stesso materiale e della stessa massa a contatto tra di loro e isolati dall’intorno.
Sapendo che uno si trova ad una temperatura di 197◦C e l’altro ad una temperatura di 130◦C, determinare:
(a) la temperatura di equilibrio; (b) la variazione di entropia del corpo 1, del corpo 2 e la variazione totale; (c)
la variazione di energia interna totale. (Sia C̄V = 24.5 Jmol−1 K −1 non dipendente da T ).
Soluzione
(a) Le temperature in gioco sono: T1 =197◦ C=470.15K e T2 =130◦ C=403.15K. Il calore perso dal blocco piu’
caldo dovra’ eguagliare il calore assorbito dal blocco piu’ freddo, ossia:
Cv (T1 − Te ) = Cv (Te − T2 )
da cui
T1 +T2
2
Te =
= 436.65K = 163.5◦ C
(b) Sappiamo che
dS =
quindi
∆S =
Z
T2
T1
δq
dU
Cv dT
=
=
T
T
T
Cv
dT = Cv
T
30
Z
T2
T1
T2
dT
= Cv ln .
T
T1
Per il corpo inizialmente piu’ caldo si ha che Tc = T1 e Tf = (T1 + T2 )/2 quindi
∆Sc = Cv ln
T1 + T 2
= −1.81Jmol−1K −1 .
2T1
Analogamente per il corpo inizialmente piu’ freddo si ha
∆Sf = Cv ln
T1 + T 2
= 1.95Jmol−1K −1 .
2T2
La variazione di entropia totale sara’ invece data da
∆S = ∆Sc + ∆Sf = Cv ln
(T1 + T2 )2
= 0.14Jmol−1 K −1 .
4T1 T2
(c) Il sistema é isolato quindi ∆U = 0 (∆U1 = −∆U2 ).
Compito II, esercizio 1.
Siano dati due blocchi dello stesso materiale e della stessa massa a contatto tra di loro e isolati dall’intorno.
Sapendo che uno si trova ad una temperatura di 167◦C e l’altro ad una temperatura di 130◦C, determinare:
(a) la temperatura di equilibrio; (b) la variazione di entropia del corpo 1, del corpo 2 e la variazione totale; (c)
la variazione di energia interna totale. (Sia C̄V = 24.5 Jmol−1 K −1 non dipendente da T ).
Soluzione
(a) Te = 421.65 K = 148.5◦ C .
(b) ∆Sc = −1.05 Jmol−1 K −1 .
(c) ∆Sf = 1.10 Jmol−1 K −1 .
(d) ∆S = 0.048 Jmol −1 K −1 .
(e) ∆U = 0 .
4. Una mole di gas ideale monoatomico a V =20 l e T =278 K raddoppia il suo volume a T costante in modo
reversibile. (a) Quanto e’ il lavoro di espansione? (b) Il sistema assorbe o emette calore? (c) Quanto vale ∆H?
(d) Quanto vale ∆P ? (e) e ∆T ?
Soluzione
(a) Siamo in presenza di un’espansione reversibile isoterma. Per un gas ideale U ≡ U (T ); in questo caso
∆T = 0, quindi ∆U = 0. Allora, dal primo principio della termodinamica q = −w. Sapendo che δw = −P dV
e che per un gas ideale P = nRT
V , si ha
nRT
δw = −
dV
V
che integrata diventa
Vf
w = −nRT ln
.
Vi
Sostituendo i valori numerici seguenti
V1 = 20l;
V2 = 40l;
T = 278K;
R = 0.082058l · atm · mol −1 · K −1
per una mole di gas si ottiene
w = −15.8121 l · atm = −1.602 kJ/mol .
31
(b) Il lavoro é negativo perché é il gas che compie lavoro, mentre q(= −w) é positivo perché é entrata energia
sotto forma di calore per mantenere la temperatura costante, dato che il sistema ha usato la sua energia per
compiere il lavoro. Il sistema quindi assorbe calore.
(c) Consideriamo la definizione di entalpia
∆H = ∆U + ∆(P V )
che per un gas ideale diventa
∆H = ∆U + ∆(nRT ) = ∆U + nR∆T
ma per una trasformazione isoterma ∆U = 0 e ∆T = 0 da cui
∆H = 0 .
(d) Partendo come al punto precedente dalla definizione di entalpia e sfruttando il risultato ottenuto si ha che
∆(P V ) = P ∆V + V ∆P = 0
separando le variabili, integrando come segue
∆P = −
P
∆V = −
V
Z
V2
V1
h1
1i
nRT
dV = −nRT
−
2
V
V1
V2
considerando una mole di gas e sostituendo i valori numerici dati dal problema si ha
∆P = −0.5703 atm = −0.5778 bar = −57.78 kP a .
(e) Essendo la trasformazione isoterma, ovviamente si ha che
∆T = 0 .
Compito II, esercizio 4.
Una mole di gas ideale monoatomico a V =10 l e T =248 K raddoppia il suo volume a T costante in modo
reversibile. (a) Quanto e’ il lavoro di espansione? (b) Il sistema assorbe o emette calore? (c) Quanto vale ∆H?
(d) Quanto vale ∆P ? (e) e ∆T ?
Soluzione
(a) w = −14.10581 l · atm = −1.429 kJ/mol .
(b) idem: il sistema assorbe calore .
(c) ∆H = 0 .
(d) ∆P = −1.0175 atm = −1.0309 bar = −103.09kP a .
(e) ∆T = 0 .
5. Lo stesso gas dell’esercizio precedente si espande adiabaticamente in modo reversibile: (a) quanto vale ∆T ?
(passaggi!). Ricordare che Cv = 3/2R e che ci si riferisce ad una mole.
Soluzione
(a) Siamo in presenza di un’espansione reversibile adiabatica: non c’é scambio di calore (q = 0) e vale
∆U = w = CV ∆T . ∆T si può ottenere tenendo conto che dU = δw, che si può anche scrivere come C V dT =
−P dV . Per un gas ideale P = RT
V e si ha
RT
dV
CV dT = −
V
32
da cui
dT
R dV
=−
T
CV V
Integrando tra (Ti , Vi ) e (Tf , Vf ) e tenendo conto che
Z
ln
da cui, ponendo
CV
R
Tf
Ti
R
CV
non dipende dal volume, si ottiene
R
dT
=−
T
CV
Z
Vf
Vi
Tf
R
Vf
=−
ln
= ln
Ti
CV
Vi
dV
V
Vi
Vf
CR
V
= γ, si ricava
Tf
=
Ti
Vi
Vf
Vi
Vf
γ1
quindi
Tf =
γ1
Ti
Notiamo che siamo in presenza di un gas ideale quindi Cv = 32 R. Sostituendo i valori numerici dati si ha quindi
20l (2/3)
Tf = 278K ·
40l
ossia:
= 175.129 K
∆T = −102.87K
da cui si evince che la temperatura per la trasformazione considerata, diminuisce .
Compito II, esercizio 5.
Lo stesso gas dell’esercizio precedente si espande adiabaticamente in modo reversibile: (a) quanto vale ∆T ?
(passaggi!). Ricordare che Cv = 3/2R e che ci si riferisce ad una mole.
Soluzione
(a) Tf = 156.23K ossia: ∆T = −91.77K
6. Con riferimento all’esercizio precedente si calcolino le variazioni di P , U e H
Soluzione
RTi
= 1.155 bar
Vi
RTf
= 0.364 bar
Pf =
Vf
Pi =
e quindi
∆P = −0.791 bar .
Dal punto precedente
∆T =
"
Vi
Vf
32
−1
#
Ti = −102.871K
quindi
∆U = Cv ∆T = 32 R∆T = −12.66 l · atm = −1.282kJ/mol .
33
Per calcolare la variazione di entalpia, ricordiamone ancora una volta la definizione e sfruttiamo la condizione
di adiabaticitá e la legge dei gas ideali, ottenendo
∆H = ∆U + ∆(P V ) = Cv ∆T + R∆T = ∆T
3
5
R + R = ∆T R = -21.103 l · atm = −2.138 kJ/mol
2
2
Compito II, esercizio 6.
Con riferimento all’esercizio precedente si calcolino le variazioni di P , U e H
Soluzione
Pi = 2.062 bar
Pf = 1.031 bar
e quindi
∆P = −1.031 bar .
∆U = −11.29 l · atm = −1.144 kJ/mol
∆H = −18.826 l · atm = −1.907 kJ/mol
7. Quanto vale ∆S: (a) nel caso dell’esercizio 4; (b) e nel caso dell’esercizio 5; (c) quanto vale ∆G in entrambi
i casi?
Soluzione
(a) Per il secondo principio della termodinamica
q
−w
∆S =
=
=
T
T
Z
V2
V1
V2
RT
dV = Rln
= 8.3145 ln2Jmol −1 K −1 = 5.7632 Jmol −1 K −1
TV
V1
o anche, essendo ∆U = 0 e sfruttando il risultato ottenuto per il lavoro nell’esercizio 4 si ha:
∆S =
1.602kJ/mol
q
=
= 5.7632 Jmol −1 K −1
T
278K
(b) Essendo la trasformazione adiabatica q = 0 quindi ∆S=0 .
(c) Nel caso dell’esercizio 4, si aveva T = cost; quindi da G = H − T S, possiamo scrivere ∆G = ∆H − T ∆S.
Per un gas ideale, se T = cost ∆H = 0; inoltre abbiamo appena visto che ∆S = 5.7632 Jmol −1 K −1 . Quindi
∆G = −278K · 5.7632 Jmol −1 K −1 = -1602 Jmol −1 .
Nel caso dell’esercizio 5 si ha invece ∆H = −2.138 kJ/mol e ∆S = 0 quindi ∆G = ∆H .
Compito II, esercizio 7.
Quanto vale ∆S: (a) nel caso dell’esercizio 4; (b) e nel caso dell’esercizio 5; (c) quanto vale ∆G nei due casi?
Soluzione
∆S = 5.7632 Jmol −1 K −1 .
∆S = 0 .
∆G = −1429 J/mol .
34
∆H = −1.907 kJ/mol e ∆S = 0 quindi ∆G = ∆H .
8. Le entalpie di combustione a 25◦ C di metanolo liquido, CH3 OH, idrogeno gassoso e grafite, per formare
CO2 (g) e H2 O(l), sono rispettivamente: 726.0 kJ/mol, 285.8 kJ/mol e 393.5 kJ/mol. Scrivere le reazioni corrispondenti alla combustione dei tre composti (es. H2 (g) + 12 O2 (g) → H2 O(l)) e poi la reazione di formazione
del metanolo liquido, infine combinarle e calcolare l’entalpia di formazione ∆Hf0 per il metanolo liquido a 298.15
K.
Soluzione
Le reazioni in gioco sono
(1)
(2)
(3)
CH3 OH(l) + 23 O2 (g) → CO2 (g) + 2 H2 O(l)
H2 (g) + 12 O2 (g) → H2 O(l)
C(s) + O2 (g) → CO2 (g)
∆Hc0 = 726.0 kJ/mol
∆Hc0 = 285.8 kJ/mol
∆Hc0 = 393.5 kJ/mol
(4)
C(s) + 2 H2 (g) + 12 O2 (g) → CH3 OH(l)
∆Hf0 = ?
Per calcolare ∆Hf0 (298.15 K) del metanolo liquido si può usare la legge di Hess e combinare le reazioni a
disposizione (1-3) per ottenere la (4). In particolare, la (4) si può ottenere invertendo la reazione (1) e sommando
ad essa le reazioni (2) e (3), dopo avere moltiplicato per 2 la (2).
L’entalpia di formazione del metanolo liquido a 298.15 K, risulta quindi essere
∆Hf0 [CH3 OH(l)] = −∆Hc0 (1) + 2 · ∆Hc0 (2) + ∆Hc0 (3)
Sostituendo i dati numerici si ottiene
∆Hf0 [CH3 OH(l)] = −726.0 + 2 · 285.8 + 393.5 = 239.1 kJ/mol
Compito II, esercizio 8.
Le entalpie di combustione a 25◦ C di metanolo liquido, CH3 OH, idrogeno gassoso e grafite, per formare CO2 (g)
e H2 O(l), sono rispettivamente: 746.0 kJ/mol, 275.8 kJ/mol e 393.5 kJ/mol. Scrivere le reazioni corrispondenti
alla combustione dei tre composti (es. H2 (g) + 21 O2 (g) → H2 O(l)) e poi la reazione di formazione del metanolo
liquido, infine combinarle e calcolare l’entalpia di formazione ∆Hf0 per il metanolo liquido a 298.15 K.
Soluzione
Erano dati:
∆Hc0 = 746.0 kJ/mol
∆Hc0 = 275.8 kJ/mol
∆Hc0 = 393.5 kJ/mol
da cui si ottiene
∆Hf0 [CH3 OH(l)] = −746.0 + 2 · 275.8 + 393.5 = 199.1 kJ/mol
9. Dopo avere ricavato la relazione di Maxwell che si ottiene partendo dalla definizione di AR = U − T S, determinare come varia S in funzione di V a T costante (scrivere la relazione nella forma ∆S = ...dV ).
Soluzione
Dalla definizione A = U − T S si può ottenere in forma differenziale che dA = dU − T dS − SdT . Dal primo
principio si ha: dU = T dS − P dV , che sostituita nella relazione precedente dà:
dA = T dS − P dV − T dS − SdT
dA = −SdT − P dV
35
che indica come T e V siano le variabili naturali dell’energia interna, A = A(T, V ). Usando questo risultato,
possiamo anche esprimere dA attraverso la sua derivata totale
∂A
∂A
dT +
dV
dA =
∂T V
∂V T
Eguagliando le due equazioni si ottiene
e
∂A
∂T
∂A
∂V
= −S
V
= −P
T
Sfruttando il fatto che le derivate parziali seconde miste sono uguali
∂
∂A
∂A
∂
=
∂V T ∂T V
∂T V ∂V T
si ricava la relazione di Maxwell richiesta
∂S
∂V T
=
∂P
∂T V
.
La variazione di entropia in funzione del volume a temperatura costante e’ data da
∆S =
R V2 ∂P V1
∂T
V
dV
T = costante.
Compito II, esercizio 9.
Dopo avere ricavato la relazione di Maxwell che si ottiene partendo dalla definizione di A(AR= U − T S), determinare come varia S in funzione di V a T costante (scrivere la relazione nella forma ∆S = ...dV ).
Soluzione
idem
10. Dato il gas di van der Waals con costanti date all’esercizio 1 e sfruttando il risultato dell’esercizio precedente, determinare la variazione di entropia per la trasformazione isoterma (T = 278 K) in cui il volume viene
raddoppiato da 20 a 40 l.
Soluzione
Si tratta di determinare ∆S per una trasformazione isoterma a T = 278K e per la quale il volume passa da 20
a 40 l. Usiamo l’espressione ottenuta precedentemente
Z V2 ∂P dV.
∆S =
∂T V
V1
e riscriviamo l’equazione di van der Waals come segue
P =
RT
a
− 2
V̄ − b V̄
che deriviamo rispetto a T e sostituiamo nell’integrale
Z V2 R V̄2 − b
∆S =
dV = Rln
.
V̄ − b
V̄1 − b
V1
in cui sostituiamo i seguenti valori numerici
36
V1 =20 l;
V2 =40 l;
b=0.038577 dm3 · mol−1 ;
R=0.083145 dm3 · bar · mol−1 · K −1
ottenendo
∆S=0.05771 dm3 bar mol−1 = 5.77kJ/mol
Compito II, esercizio 10.
Si consideri il gas di van der Waals con costanti date all’esercizio 2; sfruttando il risultato dell’esercizio precedente, determinare la variazione di entropia per la trasformazione isoterma (T = 248 K) in cui il volume viene
raddoppiato da 10 a 20 l.
Soluzione
∆S=0.05779 dm3 bar mol−1 = 5.77kJ/mol .
Parte facoltativa
11. Una mole di gas (ideale, monoatomico, a T1 = 278 K) viene scaldato a volume costante (20 l.) fino a
T2 = 2T1 , di quanto aumenta U ?
Soluzione
Per il primo principio della termodinamica:
∆U = q + w = q −
Z
P dV
ma nel nostro caso il volume e’ costante quindi la precedente si riduce a
∆U = qV = Cv ∆T =
3
R∆T
2
essendo nel caso di un gas ideale e poiché la variazione di temperatura é pari a 278K si ha
∆U = 3.47 kJ/mol
con R = 8.3145 Jmol −1 K −1 .
Compito II, esercizio 11.
Una mole di gas (ideale, monoatomico, a T1 = 248 K) viene scaldato a volume costante (10 l) fino a T2 = 2T1 ,
di quanto aumenta U ?
Soluzione
∆U = 3.09 kJ/mol .
12. Una mole di gas (ideale, monoatomico, a T1 = 278 K) viene scaldato a volume costante (20 l.) fino a
T2 = 2T1 , di quanto aumentano P , H ed S?
Soluzione
Calcoliamo la variazione di P .
Sfruttando la legge dei gas perfetti si ha che
37
Pi =
nRTf
Vf
Pf =
nRTi
Vi ;
i
= nR2T
Vi ;
da cui si ottiene
∆P = Pf − Pi = nR
e anche:
T
f
−
Vf
∆P = Pf − Pi = nR
Ti Vi
Ti
Vi
ma Vf = Vi = V = 20 l quindi
∆P =
nR
V ∆T
= 1.141atm = 1.156 bar = 115.6 kP a
con R = 0.082058 l · atm · mol −1 · K −1 .
Calcoliamo la variazione di entalpia.
∆H = ∆U + ∆(P V ) = ∆U + nR∆T = 3.47 · 10+3 J/mol + 8.3145Jmol −1K −1 · 278K = 5.78 kJmol −1
In altro modo si puó dire che ∆H = Cp ∆T con Cp − CV = R.
Calcoliamo la variazione di entropia.
∆S =
Z
T2
T1
CV
T2
dT = CV ln
= 8.643 Jmol−1 K −1
T
T1
Compito II, esercizio 12.
Una mole di gas (ideale, monoatomico, a T1 = 248 K) viene scaldato a volume costante (10 l) fino a T2 = 2T1 ,
di quanto aumentano P , H ed S?
Soluzione
∆P = 2.03atm = 2.056 bar = 205.6 kP a .
∆H = ∆U + ∆(P V ) = ∆U + nR∆T = 3.09 · 103 J/mol + 8.3145Jmol −1K −1 · 248K = 5.15 kJmol −1 .
∆S = 8.643 Jmol −1 K −1 .
13.
A = U − T S, derivare rispetto a V mantenendo T costante. Usare poi i risultati per
Data larelazione
∂S
∂A
e e ∂V
ottenuti in un esercizio precedente (relativo all’equazione di Maxwell ottenuta da A) per
∂V
T T
∂U
=...
ottenere ∂V
T
Soluzione
La derivata di A rispetto a V a T costante é
∂A ∂V
Dall’esercizio 9 si aveva che
=
T
∂U
∂V
∂V
∂S
∂V
quindi l’espressione richiesta é data da
∂U T
T
=
T
∂A
∂V
T
∂S −T
∂P
∂T
∂V
V
= −P
= −P + T
38
∂P
∂T
V
T
.
Compito II, esercizio 13.
∂S
Data la relazione A = U − T S, derivare rispetto a V mantenendo T costante. Usare poi i risultati per ∂V
T
∂A
ottenuti in un esercizio precedente (relativo all’equazione di Maxwell ottenuta da A) per ottenere
e e ∂V
T
∂U
come varia U con il volume: ∂V
=...
T
Soluzione
idem.
39