Verticale
Lim(x→x0) f(x)=∞
Orizzontale
Lim(x→∞) f(x)=l
Lim(x-->∞) f(x)=∞
m=Lim(x→∞) f(x)/x
q= Lim(x→∞) (f(x)-mx)
y'>0 la funzione cresce /
y'<0 la funzione decresce \
y'=0 la funzione presenta
max,min o flesso a
tangente orizzontale
y' non esiste
6)Asintoti
Funzione continua: Lim(x→x0) f(x)=l
l=f(x0)
1° specie Lim(x→x0-) f(x) ≠ Lim(x→x0+) f(x)
Obliquo
calcolo derivata prima y'
Funzione discontinua
7)Cresce/ Decresce
Calcolo la derivata seconda y''
y">0 concavità verso l'alto
y''<0 concavità verso il basso
8)Concavità/ Convessità
D (-∞,+∞)
5)Continuità
Funzioni razionali intere
+*-/^
Funzioni algebriche
Dominio :denominatore ≠0
3° specie
Lim(x→x0-) f(x) = Lim**(x→x0+)f(x)=l finito
ma f(x0) ≠l v x0 non appartiene al dominio
Funzioni irrazionali
Radicando>0
4)Intersezione assi
asse x
y=arcsen (x)→-1 ≤x ≤1
y=arccos (x)→-1 ≤x ≤1
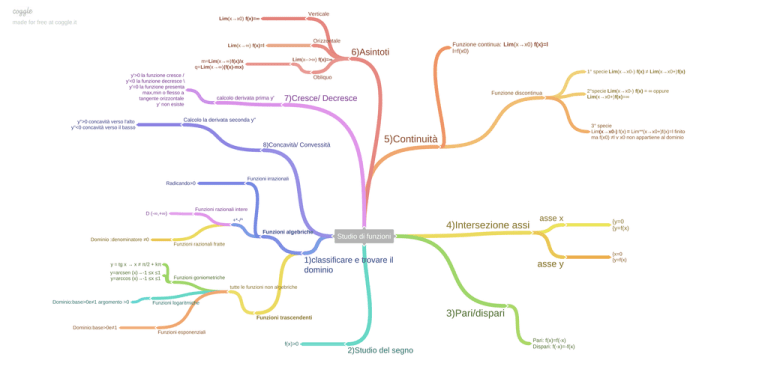
Studio di funzioni
1)classificare e trovare il
dominio
asse y
Funzioni goniometriche
tutte le funzioni non algebriche
Funzioni logaritmiche
3)Pari/dispari
Funzioni trascendenti
Dominio:base>0e≠1
{y=0
{y=f(x)
Funzioni razionali fratte
y = tg x → x ≠ π/2 + kπ
Dominio:base>0e≠1 argomento >0
2°specie Lim(x→x0-) f(x) = ∞ oppure
Lim(x→x0+) f(x) =∞
Funzioni esponenziali
f(x)>0
2)Studio del segno
Pari: f(x)=f(-x)
Dispari: f(-x)=-f(x)
{x=0
{y=f(x)











