FUNZIONI REALI DI UNA VARIABILE REALE

R. Capone
Analisi Matematica
Campo di esistenza delle funzioni reali di una variabile reale
FUNZIONI REALI DI UNA VARIABILE REALE
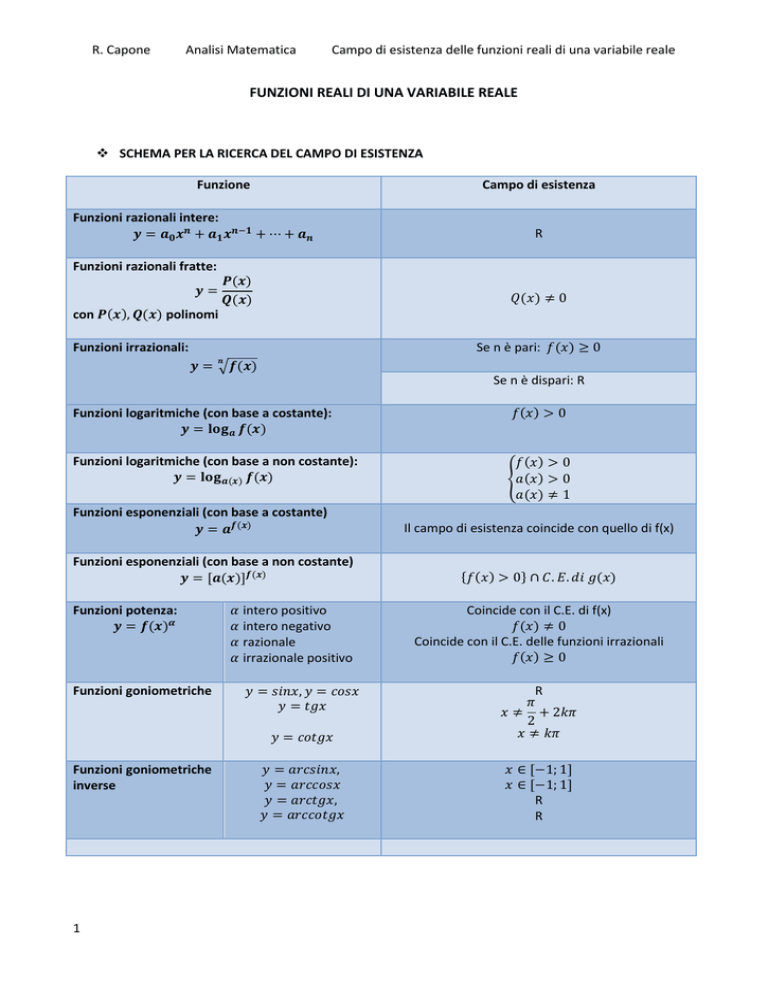
 SCHEMA PER LA RICERCA DEL CAMPO DI ESISTENZA
Funzione
Campo di esistenza
Funzioni razionali intere:
R
Funzioni razionali fratte:
con
polinomi
Funzioni irrazionali:
Se n è pari:
√
Se n è dispari: R
Funzioni logaritmiche (con base a costante):
Funzioni logaritmiche (con base a non costante):
{
Funzioni esponenziali (con base a costante)
Il campo di esistenza coincide con quello di f(x)
Funzioni esponenziali (con base a non costante)
{
Funzioni potenza:
Funzioni goniometriche
intero positivo
intero negativo
razionale
irrazionale positivo
}
Coincide con il C.E. di f(x)
Coincide con il C.E. delle funzioni irrazionali
R
Funzioni goniometriche
inverse
R
R
1
R. Capone
Analisi Matematica
Campo di esistenza delle funzioni reali di una variabile reale
Stabilisci se ciascuna delle seguenti funzioni è iniettiva, suriettiva o biettiva
1
2
3
4
5
6
7
8
√
√
9
10
Stabilisci se ciascuna delle seguenti funzioni è invertibile ed eventualmente determina l’equazione inversa
1
2
3
log
11
12
13
√
4
14
5
15
6
16
√
√
7
8
9
10
17
√
18
19
20
Ciascuno dei seguenti grafici rappresenta una funzione
funzione iniettiva, suriettiva, biiettiva.
2
. Indica per ognuno se si tratta di una
R. Capone
Analisi Matematica
Campo di esistenza delle funzioni reali di una variabile reale
Date le seguenti funzioni f e g, determina
e
:
1
f x   2 x 2  1 ; g  x   x  1 .
 f g  x   2 x  3;  g f  x   2 x 2  2 


2
f  x   x  2 ; g  x   2x2  2
3
f  x   cos  3x  ; g  x   2 x  1 .
 f g  x   2 x 2  4;  g f  x   2 x  6 


 f g  x   cos  6 x  3 ;  g f  x   2 cos  3x   1


4
f  x   sen   x  ; g  x   2 x  7 .
 f g  x   sen  2 x  7 ;  g f  x   2sen   x   7 


5
f  x   3x ; g  x  
6
f  x    x  1 ; g ( x)  x  ln x .
2
ln  x  2 
.
x2





ln 3x  2 
 f g  x   3ln  x  2  ;  g f  x  

2


x
3x


 f g  x    x  ln x  12 ;  g f  x    x  12  2ln  x  1 


Data la funzione y  f  x  rappresentata nel grafico della figura sotto, disegna i grafici delle
funzioni y  f  x  , y  f  x  , y   f  x   1 , y  f   x  .
Ricerca del Campo di esistenza
Determina il campo di esistenza delle seguenti funzioni algebriche
1
2
3
4
3
√
√
]
[
R. Capone
Analisi Matematica
5
Campo di esistenza delle funzioni reali di una variabile reale
]
√ [
] √
[
[
[
√
6
7
8
9
√|
10
√
| |
√
√
11
12
13
|
√
√
√
14
√
15
16
√
√
√
√
17
18
19
20
21
22
23
24
25
26
4
| |
√
√
√
√|
|
2  5x
x  3x 2  x  3
2  3x 2
y 3 2
x  x  4x  4
x5 2
y
2x  3
y
y
y
2
x2 3
3x  2
3x  4
| 2  x | 2 x  1
2x  3
| 3  x | 3 x  1
x 3
y 2
2x  x 1
2x
y
x2  9
5x
y 2
3x  2 x
y
 x  1  x  3
5
 x  2  x  1
3

 x  2 
2

 x  3 
4


 x  3  x  3
3


 x  2  x  2
1
x  1  x 
2
x  3  x  3
x0  x
2
3
] √ [
]√
[
R. Capone
27
Analisi Matematica
Campo di esistenza delle funzioni reali di una variabile reale
x 1
y
x
28
2 x2  x
y  x2  x  3
x3
29
y  3x  2  x
x
1
 x0
2
2
3
30
√
Determina il campo di esistenza delle seguenti funzioni trascendenti contenenti funzioni esponenziali
e/o logaritmiche
1
√
2
3
4
5
R
√l
√
6
√
7
8
√
9
10
11
√
(
)
log
√
√ log
√
12
log
log
|
|
(
|
13
)
|
14
√
15
(
)
16
√
17
18
√
√
19
√log
20
log log
log
21
log
log
22
5
log
log
log
log
]
log
log
log
[
log
R. Capone
Analisi Matematica
23
log
24
log
Campo di esistenza delle funzioni reali di una variabile reale
[
√
25
√
√
(
)
26
√
(
)
log
27
√
(
)
o
28
log log
29
log
log
30
√
√
Determina il campo di esistenza delle seguenti funzioni di vario tipo
1
√
2
√
√
3
log
4
√
log
√
5
√
6
√
√
7
8
9
+
√log
10
11
√
12
6
√
√
]
R. Capone
13
Analisi Matematica
√
14
15
(
)
√
16
√
(
)
17
√
√
18
(
)
(
)
19
√
20
log |
21
log
|
|
|
22
√
23
24
|
log | |
log |
|
|
|
|
|
|
25
|
|
26
27
log |
28
log
29
log |
30
log
Ulteriori esercizi
1
2
√
7
|
|
|
|
|
|
|
|
|
|
|
|
Campo di esistenza delle funzioni reali di una variabile reale
R. Capone
Analisi Matematica
3
√
4
√
Campo di esistenza delle funzioni reali di una variabile reale
5
√
6
(
|
√
√
)
√
|
| |
7
√
√
8
√
9
√
10
log |
√
log |
[
11
√
12
√
] √ √ [
|
[
[
|
[
13
[
(
[
[
[
)
14
√
(
[
)
√
√
[
15
√
| |
16
17
18
19
20
21
22
√
√ |
|
{ }
√log
| |
√
|
√
√
]
23
√
24
25
8
R
|
√
(
)
√
[
[√
[
R. Capone
Analisi Matematica
26
√log
27
log
28
√
29
√
log
|
Campo di esistenza delle funzioni reali di una variabile reale
√ log
|
]
[
]
[
√
30
√
31
log
(√
√
)
]
[
32
33
√
√
34
√log
35
√
36
]
√
37
38
√
√
[
√
39
√
| |
40
√
41
log
42
log
43
log
44
log
45
√
log
√
(
)
BIBLIOGRAFIA
L. Sasso - “Nuova matematica a colori” – Petrini
D’Apice-Manzo – “Verso l’esame di matematica” – CUES
9
[
[
R. Capone
Analisi Matematica
Campo di esistenza delle funzioni reali di una variabile reale
Bergamini-Trifone-Barozzi “Matematica.blu.2.0” – Zanichelli
Renato Fiorenza – Esercitazioni di analisi matematica vol.1 – Liguori editore
10