Introduzione alla Statistica Elementi di calcolo delle probabilità

Introduzione alla Statistica
Corso di Misure Meccaniche e Termiche
Prof. Ing. David Vetturi
Elementi di calcolo delle
probabilità
• Il calcolo delle probabilità ha avuto origine con i
giochi d’azzardo per valutare l’alea (casualità) legata
alle puntate sui dadi e sulle carte da gioco
• Attualmente il calcolo delle probabilità trova
applicazioni in numerose discipline tecniche e
scientifiche
• Il concetto di probabilità trova rispondenza nel
linguaggio comune senza necessità di definizioni:
“Prendi l’ombrello, è probabile che oggi piova”
• E’ necessario tuttavia definire la probabilità in
termini matematici (“numerici”) al fine di poter
trattare questo concetto naturale anche in modo
quantitativo
• Esistono diverse formulazioni del concetto di
probabilità che nel corso del tempo sono state
proposte, classificabili in due categorie:
– definizione con criteri oggettivi;
– definizione con criteri soggettivi, cioè basati sulla
percezione individuale di una realtà fisica.
Definizione a priori della
probabilità (o classica)
– La probabilità di un evento E è definita come il
rapporto tra il numero s dei risultati favorevoli (cioè
il numero dei risultati che determinano E) ed il
numero n dei risultati possibili:
PE  
s
n
purché i risultati siano tutti ugualmente possibili e
tra loro incompatibili
1
Definizione assiomatica di
probabilità
• Le definizioni di probabilità fin qui presentate
non sono in generale utilizzabili per vari motivi.
• Per ovviare a questa assenza di generalità delle
definizioni presentate la scelta preferibile sul
piano teorico (non operativo in generale) è
quella di utilizzare una definizione assiomatica
di probabilità.
– Si dice fenomeno casuale (o aleatorio) un fenomeno
empirico il cui risultato non è prevedibile a priori,
caratterizzato cioè dalla proprietà che la sua
osservazione in un insieme fissato di circostanze
non conduce sempre agli stessi risultati
– L’insieme costituito da tutte le osservazioni
possibili, cioè tutti i risultati possibili a priori, viene
detto spazio campione S (Sample Space)
– Definiamo un evento E un sottoinsieme di S
– Nella loro totalità gli eventi formano lo spazio degli
eventi A
E
S
E
Diagramma di Venn
EF
F
S
Evento intersezione
– Due eventi E ed F si dicono incompatibili o
mutuamente escludentisi se gli insiemi delle loro
descrizioni sono disgiunti, cioè se
EF  E  F  
E
F
S
Eventi incompatibili
2
Assiomi di Kolmogoroff
• Una funzione di probabilità P è una funzione di
insieme che ha come dominio lo spazio degli
eventi, come codominio l’intervallo [0,1] e che
soddisfa i seguenti assiomi:
P E   0
PS   1
E  A
Esempio
Consideriamo il lancio di una coppia di dadi
– Sia l’evento E=“la somma dei numeri dei due dadi
non sia superiore a 8”
– Sia l’evento F=“compaia almeno un 5”
P  Ei    PEi 
i  i
– Dato uno spazio di probabilità (S, A, P[.]) si
definisce probabilità condizionata dell’evento E
dato l’evento F, con E ed F eventi qualunque di A,
il rapporto:
PE F  
PEF 
PF 
con PF   0
2
3
4
5
6
7
8
3
4
5
6
7
8
9
4
5
6
7
8
9
10
5
6
7
8
9
10
11
6
7
8
9
10
11
12
Risultato del dado
evento E
PE  
con Ei eventi (di A) che si escludono a vicenda
Probabilità Condizionata
1
2
3
4
5
6
7
1
2
3
4
5
6
26
36
PF  
evento F
11
36
Esempio
Se si volesse calcolare quale sia la probabilità
dell’evento E=“la somma dei numeri dei due dadi
non sia superiore a 8” condizionato all’evento
F=“compaia almeno un 5”, allora
6
PE F  
11
1
2
3
4
5
6
1
2
3
4
5
6
7
2
3
4
5
6
7
8
3
4
5
6
7
8
9
4
5
6
7
8
9
10
5
6
7
8
9
10
11
Risultato del dado
evento E
evento F
6
7
8
9
10
11
12
6
PEF  36 6
PE F  


PF  11 11
36
3
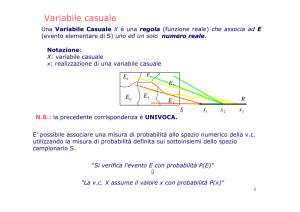
Variabili casuali
Funzione di distribuzione cumulativa
Assegnato uno spazio di probabilità (S, A, P[.]) si
definisce variabile casuale X una funzione avente
come dominio lo spazio dei campioni (S) e come
codominio la retta reale.
S
X
Le variabili casuali si indicano
con lettere maiuscole X
Data una variabile casuale X, si definisce funzione di
distribuzione cumulativa FX(x) la funzione che ha per
dominio l’asse reale e per codominio l’intervallo
chiuso [0,1] così definita:
FX  x   P X  x 
x
Variabili casuali
• Definiamo una variabile casuale discreta se
questa assume valori discreti
• Definiamo una variabile casuale continua se
questa può assumere con continuità tutti i valori
di R (asse reale)
Funzione di densità discreta
Data una variabile casuale discreta X con
codominio=(x1, x2, x3, … xn), si definisce funzione di
densità discreta fX(x) (o funzione di probabilità) la
funzione così definita:
 P X  x j 
f X x  
0

se x  x j
se x  x j
4
Funzione di densità discreta
Funzione di densità di probabilità
La funzione di densità discreta fX(x) ha le seguenti
proprietà:
f X x   0
Analogamente a quanto appena visto, la funzione di
densità di probabilità fX(x) ha le seguenti proprietà:
x
 f X  xi   1
i
FX  x    f X  xi 
f X x  0
x
 f X  x  dx  1

 FX  xi   lim FX  xi  h 
h0
f X x   
0

i:xi  x

se x  xi
Funzione di densità di probabilità
Data una variabile casuale continua X, si definisce
funzione di densità di probabilità di X fX(x) la
funzione tale per cui:
FX  x    f X t   dt
x
Pa  X  b  a f X  x  dx
se x  xi
b
Esempio
Consideriamo il lancio di un dado e l’estrazione di una pallina da
un’urna contenente 2 palline rosse, 3 blu e 5 verdi.
Attribuiamo all’estrazione della pallina il valore 5 se questa è
rossa, 3 se blu e 1 se verde.
Consideriamo la variabile casuale X data dalla somma del risultato
del dado con il valore della pallina estratta.
d
a
d
o
1
2
3
4
5
6
R
6
7
8
9
10
11
5
R
6
7
8
9
10
11
B
4
5
6
7
8
9
3
B
4
5
6
7
8
9
pallina
B
4
5
6
7
8
9
V
2
3
4
5
6
7
V
2
3
4
5
6
7
1
V
2
3
4
5
6
7
V
2
3
4
5
6
7
V
2
3
4
5
6
7
X
2
3
4
5
6
7
8
9
10
11
Ni
5
5
5
5
5+3
8
5+3
8
5+3+2 10
5+3+2 10
3+2
5
3+2
5
2
2
2
2
P(X)=f(x)
0.083
0.083
0.133
0.133
0.167
0.167
0.083
0.083
0.033
0.033
F(x)
0.083
0.167
0.300
0.433
0.600
0.767
0.850
0.933
0.967
1.000
5
Esempio
Varianza
fx(X)
0.2
0.18
Ni
5
5
5
5
5+3
8
5+3
8
5+3+2 10
5+3+2 10
3+2
5
3+2
5
2
2
2
2
P(X)=f(x)
0.083
0.083
0.133
0.133
0.167
0.167
0.083
0.083
0.033
0.033
F(x)
0.083
0.167
0.300
0.433
0.600
0.767
0.850
0.933
0.967
1.000
Si definisce varianza della variabile casuale X con
media x la funzione:
fx(X)
0.08
0.06
0.04
0.02
0
0
1
2
3
4
5
6
7
8
X
9
 X2    xi   X 2  f X  xi 
10 11 12 13 14 15
1

2
X
Fx(X)
0.8
i
    x   X 2  f X  x   dx
1.2
Fx(X)
X
2
3
4
5
6
7
8
9
10
11
0.16
0.14
0.12
0.1
0.6
0.4
0.2
0
0
1
2
3
4
5
6
7
X
8
9 10 11 12 13 14 15
Media
Esempio
Consideriamo nuovamente il problema legato al lancio di un dado
e all’estrazione di una pallina da un’urna contenete 2 palline rosse,
3 blu e 5 verdi.
Considerata la variabile casuale X come prima definita.
n
Si ha:
Si definisce media, o valore atteso, della variabile
casuale X la funzione:
E  X    xi  f X  xi 
E  X    xi  f X ( xi )  5.9
i 1
   xi  E X 2  f X ( xi )  5.357  X  2.31
2
X
i
E  X    x  f X  x   dx

d
a
d
o
1
2
3
4
5
6
R
6
7
8
9
10
11
5
R
6
7
8
9
10
11
n
i 1
B
4
5
6
7
8
9
3
B
4
5
6
7
8
9
pallina
B
4
5
6
7
8
9
V
2
3
4
5
6
7
V
2
3
4
5
6
7
1
V
2
3
4
5
6
7
V
2
3
4
5
6
7
V
2
3
4
5
6
7
X
2
3
4
5
6
7
8
9
10
11
Ni
5
5
5
5
5+3
8
5+3
8
5+3+2 10
5+3+2 10
3+2
5
3+2
5
2
2
2
2
P(X)=f(x)
0.083
0.083
0.133
0.133
0.167
0.167
0.083
0.083
0.033
0.033
F(x)
0.083
0.167
0.300
0.433
0.600
0.767
0.850
0.933
0.967
1.000
6
Ni
5
5
5
5
5+3
8
5+3
8
5+3+2 10
5+3+2 10
3+2
5
3+2
5
2
2
2
2
P(X)=f(x)
0.083
0.083
0.133
0.133
0.167
0.167
0.083
0.083
0.033
0.033
F(x)
0.083
0.167
0.300
0.433
0.600
0.767
0.850
0.933
0.967
1.000
0.16
0.14
0.12
0.1
fx(X)
0.08
0.06
0.04
0.02
0
0
1
2
3
4
5
6
7
X
8
9
10 11 12 13 14 15
1.2
1
0.4
0.2
0
1
2
3
4
5
6
7
X
8
P X   x     x   1 
1
2
9 10 11 12 13 14 15
Deviazione Standard
Si definisce come deviazione standard o scarto
quadratico medio o scarto tipo (della variabile
casuale X) la radice quadrata della varianza, cioè:
 X   X2
Sia X variabile casuale a varianza finita.
Allora si ha:
P x     x  X   x     x   1 
0.6
0
• Corollario della disuguaglianza di Tchebycheff
o equivalentemente:
Fx(X)
0.8
Fx(X)
X
2
3
4
5
6
7
8
9
10
11
Disuguaglianza di Tchebycheff
0.2
0.18
fx(X)
 X  5.9  X  2.31
Esempio
1
2
Distribuzioni discrete
La variabile casuale X ha distribuzione uniforme
discreta se la sua funzione di densità discreta è data
da:
 1
f X x   N
 0
Si dimostra che:
E X  
N 1
2
per x  1,2,.., N
altrove
 x2 
N 2 1
12
7
Distribuzioni binomiale
La variabile casuale X ha distribuzione binomiale se
la sua funzione di densità discreta è data da:
 n   p x  (1  p ) n x
f X  x    x 

0
Si dimostra che:
E X   n  p
per x  0,1,2,.., n
altrove
 x2  n  p  1  p 
Distribuzioni binomiale
• Esempio
Consideriamo la variabile X relativa al lancio di una
moneta 3 volte dove con X si indica il numero di
volte in cui risulta testa.
T
C
T
C
T
C
C
C
T
T
T
C
T
C
X=3
X=2
X=2
X=1
X=2
X=1
X=1
X=0
1
f x ( 0) 
8
3
f x (1) 
8
3
f x ( 2) 
8
1
f x (3) 
8
Distribuzioni binomiale
Utilizzando la distribuzione binomiale con:
• p=0.5
• n=3
 n   p x  (1  p ) n x
f X  x    x 

0
per x  0,1,2,.., n
Si ha:
altrove
1
8
3
f x ( 2) 
8
f x ( 0) 
 3   1 0  1 3
f x ( 0)         
 0  2   2 
 
3
8
1
f x (3) 
8
f x (1) 
Distribuzioni ipergeometrica
La variabile casuale X ha distribuzione
ipergeometrica se la sua funzione di densità discreta è
data da:
 K    M  K 
 x   n  x 

f X x   
M 
n

 

0
Si dimostra che:
E X   n 
K
M
 x2  n 
per x  0,1,2,.., n
altrove
K M K M n


M
M
M 1
8
Distribuzioni ipergeometrica
• Esempio
Consideriamo una fornitura di 30 PC portatili di cui 6
presentano un difetto allo schermo.
Esaminandone 10, qual è la probabilità di averne 3
con quel difetto?
M  30
K 6
 6    30  6 
 x   10  x 

f X x    
30
 
 10 
 
n  10
f X 3  0.23039
Distribuzioni ipergeometrica
• Utilizzo di Excel
Tornando all’esempio:
M  30
K 6
n  10
Distribuzioni di Poisson
La variabile casuale X ha distribuzione di Poisson se
la sua funzione di densità discreta è data da:
 e   x

f X  x    x!
 0
Si dimostra che:
EX   
per x  0,1,2,.., n,..
altrove
 x2  
Distribuzioni continue
La variabile casuale X ha distribuzione uniforme
(continua) nell’intervallo [a,b] se la sua funzione di
densità di probabilità è data da:
 1
f X  x   b  a
 0
fx(x)
a
per a  x  b
altrove
b
x
9
Media
Distribuzioni uniforme
E x    x   x  f x ( x )dx 

Distribuzioni uniforme
Varianza
  x  f x ( x) dx  a x  f x ( x)dx  b x  f x ( x)dx 
a
b

1

dx  b x  0 dx 
ba
b
1 b
1  x2 

x
dx



ba a
b  a  2  a
  x  0 dx  a x 
a

b
1  b 2  a 2  b  a b  a  b  a



b  a  2 
2b  a 
2
Distribuzioni uniforme
Varianza
 x2   x 2  f x ( x )dx   x2

2
2
2
 x  f x ( x)dx  a x  f x ( x)dx  b x  f x ( x)dx 
a
b

1

dx  b x 2  0 dx 
ba
b
1 b 2
1  x3 

 x dx  b  a  3  
ba a
 a

b 2  ab  a 2  b  a 

 
3
 2 
2
b 2  ab  a 2 b 2  2ab  a 2


3
4
4b 2  4ab  4a 2   3b 2  6ab  3a 2 

12
2
b 2  2ab  a 2 b  a 


12
12

Distribuzione esponenziale
La variabile casuale X ha distribuzione esponenziale
(negativa) se la sua funzione di densità di probabilità
è data da:
b
1  b 3  a 3  b  a b 2  ab  a 2  b 2  ab  a 2



b  a  3 
3b  a 
3

 x2 
  x 2  0 dx  a x 2 
a
 x2   x 2  f x ( x )dx   x2
  x

f X  x     e
 0
con:
  R
cioè
per x  0
per x  0
 0
10
Distribuzione esponenziale
Si dimostra che:
 
2
x

1
2
fx(x)
E X    x 
1
0
x
Variabile casuale funzione di
variabile casuale
In molti casi si fa uso di trasformazione di
variabili casuali.
Sia X variabile casuale con funzione di densità di
probabilità fX(x) assegnata.
Sia Y una variabile casuale funzione di X con
Y=g(X).
Ovviamente è possibile calcolare media e
varianza di Y nota la sua funzione densità di
probabilità fY(y).
Trasformazione di variabile
casuale Y=g(X)
Riferimento:
G. Vicario, R. Levi, “Statistica e probabilità per ingegneri”,
Esculapio (Bologna) - Paragrafo. 3.3 - pag. 104
Ci siamo già occupati del problema riguardante una
variabile casuale Y funzione di una assegnata
variabile casuale X
Un teorema ci consente di calcolare la funzione di
densità di probabilità di Y nota la funzione di densità
di probabilità di X ed il legame fra Y ed X, cioè
Y=g(X)
Trasformazione di variabile
casuale Y=g(X)
• Teorema 3.17
Sia X una variabile casuale continua con funzione di
densità di probabilità fx(x). La variabile casuale
Y=g(X) è continua ed inoltre
f y  y 
d 1
g  y   f x g 1  y 
dy
dove y=g(x) è una trasformazione biunivoca da Dx in
Dy e d 1
dy
g
y  0
e continua
y  D y
11
Trasformazione di variabile
casuale Y=g(X)
Y=g(X)
Variabile casuale funzione di
variabile casuale
Si dimostra che, se Y=g(X), allora:
Y  EY    y  fY  y   dy  EY Y 

fx(x) y

fx(x)
Y   g ( x)  f X x   dx  E X g ( X )


Teorema della media
x
Trasformazione di variabile
casuale Y=g(X)
• Osservazione
Decomponendo Dx in un insieme di sottoinsiemi Dxi
disgiunti tali per cui y=g(x) sia biunivoca fra ciascun
Dxi e Dyi allora
f y  y  
i
d 1
g i  y   f x g i1  y 
dy
Variabile casuale funzione di
variabile casuale
Si dimostra che, se Y=g(X), allora:


 2Y  E Y  Y 2  
 2Y  

2

y  Y   fY  y   dy


g ( x)  Y 2  f X x   dx
 2Y  EY Y 2  Y 2  E X g ( x) 2  Y 2

Teorema della media
(caso della varianza)
12
Distribuzione normale
(di Gauss)
La variabile casuale X ha distribuzione normale (o
distrubuzione di Gauss) se la sua funzione di densità
di probabilità è data da:
f X x 
1
2  
e
1  x 
 

2  
2
E X    x  
 
2
x
La variabile casuale X con distribuzione normale tale
per cui
 0
1
2
 1
Viene chiamata variabile casuale normale
standardizzata e comunemente è indicata con Z
1 2 x
f X x  
e
2
Distribuzione normale
(di Gauss)
Si dimostra che:
Distribuzione normale
standardizzata
1 2 z
fZ z  
e
2
1
2
2
Distribuzione normale
standardizzata
Poiché comunemente è necessario calcolare il valore
della funzione di distribuzione comulativa di Z,
questa è stata calcolata una volta per tutte.
I risultati di questa valutazione sono disponibili in
tabelle come la seguente:
fx(x)
FZ  z     z   
z

1  2u
e du
2
1
2
x
13
FZ  z     z   
z

0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0
0.00
0.50000
0.53983
0.57926
0.61791
0.65542
0.69146
0.72575
0.75804
0.78814
0.81594
0.84134
0.86433
0.88493
0.90320
0.91924
0.93319
0.94520
0.95543
0.96407
0.97128
0.97725
0.01
0.50399
0.54380
0.58317
0.62172
0.65910
0.69497
0.72907
0.76115
0.79103
0.81859
0.84375
0.86650
0.88686
0.90490
0.92073
0.93448
0.94630
0.95637
0.96485
0.97193
0.97778
z  1.53
0.02
0.50798
0.54776
0.58706
0.62552
0.66276
0.69847
0.73237
0.76424
0.79389
0.82121
0.84614
0.86864
0.88877
0.90658
0.92220
0.93574
0.94738
0.95728
0.96562
0.97257
0.97831
0.03
0.51197
0.55172
0.59095
0.62930
0.66640
0.70194
0.73565
0.76730
0.79673
0.82381
0.84849
0.87076
0.89065
0.90824
0.92364
0.93699
0.94845
0.95818
0.96638
0.97320
0.97882
0.04
0.51994
0.55962
0.59871
0.63683
0.67364
0.70884
0.74215
0.77337
0.80234
0.82894
0.85314
0.87286
0.89251
0.90988
0.92507
0.93822
0.94950
0.95907
0.96712
0.97381
0.97932
0.87493
0.89435
0.91149
0.92647
0.93943
0.95053
0.95994
0.96784
0.97441
0.97982
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0
0.00
0.86433
0.88493
0.90320
0.91924
0.93319
0.94520
0.95543
0.96407
0.97128
0.97725
0.01
0.50399
0.54380
0.58317
0.62172
0.65910
0.69497
0.72907
0.76115
0.79103
0.81859
0.84375
0.86650
0.88686
0.90490
0.92073
0.93448
0.94630
0.95637
0.96485
0.97193
0.97778
0.02
0.50798
0.54776
0.58706
0.62552
0.66276
0.69847
0.73237
0.76424
0.79389
0.82121
0.84614
0.86864
0.88877
0.90658
0.92220
0.93574
0.94738
0.95728
0.96562
0.97257
0.97831
z  0.78
  z   1    z 
0.06
0.52392
0.56356
0.60257
0.64058
0.67724
0.71226
0.74537
0.77637
0.80511
0.83147
0.85543
0.87698
0.89617
0.91308
0.92785
0.94062
0.95154
0.96080
0.96856
0.97500
0.98030
Distribuzione normale
2
0.07
0.52790
0.56749
0.60642
0.64431
0.68082
0.71566
0.74857
0.77935
0.80785
0.83398
0.85769
0.87900
0.89796
0.91466
0.92922
0.94179
0.95254
0.96164
0.96926
0.97558
0.98077
0.08
0.53188
0.57142
0.61026
0.64803
0.68439
0.71904
0.75175
0.78230
0.81057
0.83646
0.85993
0.88100
0.89973
0.91621
0.93056
0.94295
0.95352
0.96246
0.96995
0.97615
0.98124
0.09
0.53586
0.57535
0.61409
0.65173
0.68793
0.72240
0.75490
0.78524
0.81327
0.83891
0.86214
0.88298
0.90147
0.91774
0.93189
0.94408
0.95449
0.96327
0.97062
0.97670
0.98169
Se Z è una variabile casuale normale standardizzata
allora X=g(Z) con
X     Z
è una variabile casuale con normale con
E X    x  
  z  1.53  0.93699
z

0.50000
0.53983
0.57926
0.61791
0.65542
0.69146
0.72575
0.75804
0.78814
0.81594
0.84134
1
0.05
0.51595
0.55567
0.59483
0.63307
0.67003
0.70540
0.73891
0.77035
0.79955
0.82639
0.85083
FZ  z     z   
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1  2u
e du
2
0.03
0.51197
0.55172
0.59095
0.62930
0.66640
0.70194
0.73565
0.76730
0.79673
0.82381
0.84849
0.87076
0.89065
0.90824
0.92364
0.93699
0.94845
0.95818
0.96638
0.97320
0.97882
0.04
0.51595
0.55567
0.59483
0.63307
0.67003
0.70540
0.73891
0.77035
0.79955
0.82639
0.85083
0.87286
0.89251
0.90988
0.92507
0.93822
0.94950
0.95907
0.96712
0.97381
0.97932
1  2u
e du
2
1
0.05
0.51994
0.55962
0.59871
0.63683
0.67364
0.70884
0.74215
0.77337
0.80234
0.82894
0.85314
0.87493
0.89435
0.91149
0.92647
0.93943
0.95053
0.95994
0.96784
0.97441
0.97982
0.06
0.52392
0.56356
0.60257
0.64058
0.67724
0.71226
0.74537
0.77637
0.80511
0.83147
0.85543
0.87698
0.89617
0.91308
0.92785
0.94062
0.95154
0.96080
0.96856
0.97500
0.98030
Distribuzione normale
2
0.07
0.52790
0.56749
0.60642
0.64431
0.68082
0.71566
0.74857
0.77935
0.80785
0.83398
0.85769
0.87900
0.89796
0.91466
0.92922
0.94179
0.95254
0.96164
0.96926
0.97558
0.98077
0.08
0.53188
0.57142
0.61026
0.64803
0.68439
0.71904
0.75175
0.78230
0.81057
0.83646
0.85993
0.88100
0.89973
0.91621
0.93056
0.94295
0.95352
0.96246
0.96995
0.97615
0.98124
 x2   2
0.09
0.53586
0.57535
0.61409
0.65173
0.68793
0.72240
0.75490
0.78524
0.81327
0.83891
0.86214
0.88298
0.90147
0.91774
0.93189
0.94408
0.95449
0.96327
0.97062
0.97670
0.98169
  0.78   1  0.78230  0.21770
Utilizzando quanto visto precedentemente si ha:
X 
X  g (Z )      Z
Z  g 1 ( X ) 
E quindi sostituendo in
con
si ha:
f x x 
d 1
g  x   f z g 1  x 
dx
d 1
1
g ( x) 
dx


 
1
x
f x x   f z 
e 2


2 
  
1
1 x 

 
2
14