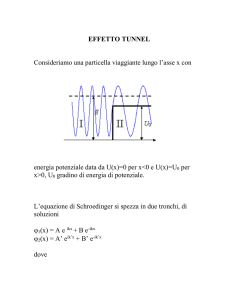
4.
La dinamica dei sistemi microscopici
I sistemi microscopici richiedono quindi una nuova sistemazione teorica
(una nuova meccanica) che sarà basata sui seguenti principi:
• Si assume come punto di partenza la relazione di De Broglie,
abbandonando il concetto classico di particella localizzata.
• La posizione di una particella sarà quindi distribuita secondo
l’ampiezza di un’onda.
• Al posto del concetto classico di traiettoria si introduce il concetto di
funzione d’onda (ψ).
• La nuova meccanica (meccanica quantistica) dovrà essere in grado
di calcolare ψ e di interpretarne il significato.
4.1 L’equazione di Schrödinger
Nel 1926 il fisico-matematico austriaco Erwin Schrödinger (esperto
di matematica delle onde) propose una equazione per la determinazione
della funzione d’onda ψ di un qualsiasi sistema quantistico.
La formula di Schrödinger è ricavata dall’equazione delle corde
vibranti di D’Alembert (XVIII secolo) e per un corpo di massa m in moto
unidimensionale con energia E assume la forma (nel caso indipendente dal
tempo):
− h 2 d 2ψ
+ V ( x )ψ = Eψ
2m dx 2
dove h =
h
= 1.05457 × 10 − 34 Js
2π
La formulazione di Schrödinger può apparire arbitraria e, in effetti,
dovrebbe essere accettata come un postulato, almeno a questo livello di
studi.
E’ tuttavia abbastanza semplice verificare che essa consente di
ottenere in modo agevole relazioni già note (=non contrasta con quanto è
già accettato).
4.1.1 Verifica: la relazione di De Broglie
Consideriamo il caso di una particella in moto unidimensionale in
una regione di potenziale costante. In questo caso, l’equazione di
Schrödinger si riduce a
d 2ψ
dx
2
=−
2m
h
2
(E − V )ψ
che ammette come soluzione generale
ψ = eikx = cos kx + i sin kx,
k = 2 m( E − V ) / h 2
Ora, cos kx o sin kx rappresentano un’onda di lunghezza λ=2π/k, dove k
prende il nome di numero d’onda 1. Essendo costante il potenziale, la
quantità (E−V) è eguale all’energia cinetica, Ek, della particella, che vale
p2
Ek =
2m
Ma poiché l’energia è legata a k dalla relazione E k = k 2 h 2 / 2m , si ha che
p = kh =
2π h
h
=
λ 2π λ
che è esattamente la relazione di De Broglie. Come si vede, l’approccio
quantistico porta esattamente ad una conclusione già nota e
sperimentalmente verificata.
E’ sufficiente confrontare cos kx con la forma standard di un’onda
armonica cos 2πx/λ
1
4.1.2 Approfondimento: la matematica dell’equazione di Schrödinger
a) Per sistemi in moto unidimensionale:
− h 2 d 2ψ
+ V ( x )ψ = Eψ
2m dx 2
b) Per sistemi in moto tridimensionale
− h2 2
∇ ψ + V (r )ψ = Eψ
2m
dove
2
∇ =
∂2
∂x
2
+
∂2
∂y
2
+
∂2
∂z 2
c) Nel caso generale, indipendente dal tempo:
Hψ = Eψ
dove H rappresenta l’operatore Hamiltoniano (l’energia totale), dato da
h2 2
H =−
∇ −V
2m
d) Nel caso generale, dipendente dal tempo:
Hψ = ih
∂ψ
∂t
4.2 L’interpretazione di Born della funzione d’onda
Occorre premettere che uno dei fondamenti della meccanica
quantistica consiste nel fatto che la funzione d’onda ψ contiene tutte le
informazioni dinamiche sul sistema che descrive.
L’interpretazione di Born ha a che fare con la localizzazione della
particella descritta dalla funzione d’onda. Essa è basata su di una analogia
con la teoria ondulatoria della luce, secondo cui il quadrato
dell’ampiezza dell’onda elettromagnetica ne determina l’intensità e
quindi, in termini quantistici, la probabilità di trovare un fotone in una
certa regione dello spazio.
Nel caso di particella in moto tridimensionale, secondo Born si ha che:
se la funzione d’onda di una particella assume un valore ψ in un punto r
dello spazio, allora la probabilità di trovare la particella in un elemento
infinitesimo di volume dτ = dx dy dz attorno al punto r è proporzionale a
ψ 2 dτ .
2
2
Si ricordi che ψ
2
= ψ *ψ
N.B. L’interpretazione di Born assegna significato fisico solo al quadrato
del modulo della funzione d’onda, che è una quantità positiva e reale. In
realtà, la presenza di regioni in cui la funzione assume valore negativo
(positivo) è di grande importanza indiretta perchè offre la possibilità di
interferenze distruttive (costruttive) tra funzioni d’onda differenti.
4.2.1 La normalizzazione della funzione d’onda
Dal punto di vista puramente matematico, se ψ è una soluzione
dell’equazione di Schrödinger allora anche Nψ lo è. E’ quindi sempre
possibile trovare un fattore di normalizzazione tale che la probabilità di
trovare la particella in un punto qualunque dello spazio sia uguale a 1.
Il fattore di normalizzazione viene determinato considerando che la
probabilità di trovare la particella in una regione dτ vale (Nψ*)(Nψ)dτ.
Inoltre, la somma su tutto lo spazio deve dare l’unità (=la certezza), per
cui si ha:
2
N
+∞
*
∫ ψ ψdτ = 1
−∞
da cui si ottiene:
N=
1
1/ 2
+∞ *
∫ ψ ψdτ
−∞
In generale, ove non sia diversamente specificato, si assume che funzioni
d’onda utilizzate siano normalizzate a 1, cioè che valga la relazione
+∞
*
∫ ψ ψdτ = 1
−∞
4.2.2 Restrizioni sulla forma della funzione d’onda
L’interpretazione di Born impone alcune restrizioni sulla forma
delle funzioni d’onda:
(a)
deve
essere
continua
(poiché
l’equazione di Schrödinger contiene la
derivata seconda di ψ);
(b)
la sua derivata prima deve essere
continua (per la stessa ragione).
(c)
deve avere un solo valore in ogni punto
dello
spazio
(altrimenti
diverse
probabilità competerebbero ad un
singolo punto);
(d)
la ψ non può andare all’infinito in
alcun punto (in caso contrario la
costante di normalizzazione dovrebbe
essere zero)3;
Inoltre:
la ψ non può essere identicamente nulla (perché la particella da qualche
parte deve pur trovarsi).
In pratica, tutte queste restrizioni fanno sì che, in generale, soluzioni
accettabili della equazione di Schrödinger non esisteranno per valori
arbitrari dell’energia, E. In altre parole, una particella potrà possedere
soltanto certi valori dell’energia (quantizzazione).
I valori accettabili dell’energia (livelli energetici) vengono ottenuti
risolvendo l’equazione di Schrödinger con il potenziale appropriato.
3
Eccezione: la delta di Dirac (funzione infinita in un solo punto).
5.
I principi della meccanica quantistica
5.1 Approccio deduttivo (formulazione assiomatica)
Assioma I
Lo stato di un sistema a n gradi di libertà è descritto da una funzione
ψ = ψ(q1, q2,…,qn, t)
delle coordinate generalizzate e del tempo, chiamata funzione d’onda. Se
ψ* rappresenta la sua complessa coniugata, allora ψ*ψdτ fornisce la
probabilità che al tempo t le coordinate generalizzate siano interne
all’elemento di volume dτ (densità di probabilità).
La funzione d’onda, per ragioni fisiche, deve essere ad un solo valore,
continua con la derivata prima e tale che il suo integrale su tutto lo spazio
sia finito. Normalmente si avrà che
∫ψ *ψdτ = 1
e la ψ prenderà il nome di funzione d’onda normalizzata.
Assioma II
Ad ogni grandezza fisica misurabile (osservabile) si associa un operatore
costruito secondo la seguente regola:
• si scrive l’espressione classica dell’operatore in termini delle
coordinate generalizzate qi, dei momenti generalizzati pi, e del
tempo.
• Nella corrispondente espressione quantistica le qi e il tempo
compaiono semplicemente come operatori di moltiplicazione, mentre
ogni momento pi è sostituito dalla espressione − ih
∂
.
∂qi
Assioma III
Per un sistema descritto dalla funzione di stato ψ i valori possibili che
possono essere ottenuti per una grandezza M, come risultato di una
misura, sono quelli che soddisfano l’equazione agli autovalori
Mψ = mψ
Dove M rappresenta l’operatore ottenuto con le regole riportate
all’assioma II, m si dice autovalore, la ψ costituisce una autofunzione
dell’operatore e lo stato da essa descritto è un autostato della grandezza M
nel senso che, in questo stato, essa assume il valore m.
5.2 Approccio induttivo (impariamo da un caso semplice)
Consideriamo il caso di una particella di massa m libera di muoversi
parallelamente all’asse x in una regione di potenziale nullo. L’equazione di
Schrödinger si riduce a
d 2ψ
dx
2
=−
2m
h
2
Eψ
(1)
la cui soluzione più generale assume la forma
ψ = Ae
ikx
+ Be
− ikx
con
h 2k 2
E=
2m
(2)
dove A e B sono costanti. Per verificare che si tratti veramente di una
soluzione della equazione, è sufficiente sostituirla al primo membro,
operare la derivazione e verificare che si ottiene Eψ.
5.2.1 La densità di probabilità
Supponiamo che nella soluzione (2) sia B = 0. Ciò corrisponde a
considerare un’onda progressiva che avanza nel verso delle x positive e
il cui momento lineare è costante. Per determinare la posizione della
particella occorre costruire il modulo quadro della funzione d’onda:
(
)(
) (
)(
)
*
ψ 2 = Ae ikx Ae ikx = A*e − ikx Ae ikx = A 2
La densità di probabilità è indipendente da x. Ciò significa che, se
la funzione d’onda è data dalla (2) con la condizione B = 0, non è
possibile determinare la posizione della particella. Lo stesso risultato
viene ottenuto ponendo A = 0 e B ≠ 0.
Se il momento lineare, p, è univocamente definito, la probabilità di
trovare la particella in un punto qualsiasi dell’asse x è una costante.
Supponiamo ora che sia A = B. Allora la soluzione (2) diviene
ψ = A(e ikx + e − ikx) = 2 A cos kx
4
e la densità di probabilità assume la forma
ψ 2 = (2 A cos kx )* (2 A cos kx ) = 4 A 2 cos 2 kx
2
In questo caso la densità di probabilità varia tra 0 e 4 A . I punti in cui la
funzione vale 0 si chiamano nodi.
La probabilità di trovare la particella in un punto esatto dello
spazio non è più costante poichè il momento lineare non è più definito
esattamente. La funzione d’onda è la somma di due stati (progressivo e
regressivo).
4
Infatti, vale la relazione
cosθ =
(
1 iθ
e + e − iθ
2
)
5.2.2 Autovalori e autofunzioni
Ricordiamo che l’equazione di Schrödinger può essere scritta nella
forma succinta
Hψ = Eψ
dove
(3)
h2 2
H =−
∇ − V (r )
2m
rappresenta l’operatore 5 Hamiltoniano (l’energia totale) in uno spazio
tridimensionale. Una equazione del tipo (3) prende il nome di equazione
agli autovalori
(operatore)×(funzione) = (fattore costante)×(medesima funzione)
Se indichiamo con Ω̂ un generico operatore e con ω un fattore costante
l’equazione assume la forma generale
Ωˆ ψ = ωψ
dove ω prende il nome di autovalore e la ψ si chiama autofunzione.
Risolvere una equazione agli autovalori significa trovare gli autovalori e
le autofunzioni dell’operatore Ω̂ .
N.B. Nel caso specifico dell’operatore Hamiltoniano, le autofunzioni sono
le funzioni d’onda e gli autovalori sono le energie permesse.
In generale, si definisce “operatore” qualcosa che esegue una operazione
matematica sulla funzione (nel nostro caso, la ψ).
5
L’importanza del formalismo delle equazioni agli autovalori nella
meccanica quantistica consiste principalmente nel fatto che lo schema
esemplificato dalla equazione di Schrödinger (3) può essere ripetuto per
altre osservabili (o quantità misurabili) del sistema quantistico, come ad
esempio il momento di dipolo elettrico o il momento lineare.
Quindi, se conosciamo sia la funzione d’onda ψ e l’operatore
corrispondente all’osservabile Ω di nostro interesse, e la funzione d’onda
è una autofunzione dell’operatore Ω̂ , allora possiamo predire il risultato
di una misura della quantità Ω semplicemente determinando il fattore ω
nell’equazione agli autovalori
Ωˆ ψ = ωψ
Nota importante:
Le autofunzioni corrispondenti a differenti autovalori dello stesso
operatore sono ortogonali, vale cioè la relazione
*
∫ψ i ψ j dτ = 0
5.2.3 Operatori
Lo studio di sistemi quantistici richiede quindi la conoscenza della
forma dell’operatore corrispondente ad una data grandezza osservabile.
Regola per le osservabili che dipendono da variabili spaziali (caso
monodimensionale):
Le osservabili sono rappresentate da operatori costruiti utilizzando i
seguenti operatori di posizione e momento lineare:
x̂ = x ×
pˆ x =
h d
d
= −ih
i dx
dx
Verifichiamo che l’espressione dell’operatore momento lineare sia
almeno sensata. Scriviamo l’equazione agli autovalori pˆ xψ = p xψ nella
forma
h dψ
= p xψ
i dx
Assumendo che la funzione d’onda abbia la forma ψ = Ae ikx si ha
h dψ h de ikx h
= A
= Aike ikx = hkAe ikx = hkψ
i dx i
i
dx
da cui si ricava 6 che
p x = hk =
6
h 2π h
= (Relazione di De Broglie)
2π λ
λ
Si ricordi che cos kx descrive un’onda di lunghezza λ=2π/k
La costruzione dell’operatore Hamiltoniano
Usiamo le regole per costruire gli operatori che contengono
variabili spaziali:
1) La parte di energia cinetica
p2
1 h d h d
h2 d2
ˆ
Ek =
→ Ek =
=−
2m
2m i dx i dx
2 m dx 2
2) La parte di energia potenziale
V ( x ) → Vˆ
(Es: V ( x ) =
1 2
1
kx → Vˆ = kx 2 )
2
2
⇓
2 2
h
d
+ Vˆ
Hˆ = Eˆ k + Vˆ = −
2
2m dx
5.2.4 Sovrapposizioni e valori di aspettazione
Consideriamo una funzione d’onda della forma
ψ = A(e ikx + e − ikx) = 2 A cos kx
se cerchiamo di calcolare il momento lineare utilizzando il formalismo
degli operatori, non otteniamo una equazione agli autovalori. Infatti:
h dψ 2h d cos kx 2kh
=
A
=
A sin kx
dx
i
i dx
i
Se forma d’onda scelta non è una autofunzione dell’operatore, allora la
proprietà corrispondente all’operatore non ha un valore definito. In
questo caso, la funzione d’onda scelta è combinazione lineare di funzioni
con stati di momento definiti
ψ = ψ → +ψ ←
Se noi misuriamo ripetutamente il momento lineare di una particella
quantistica descrittala questa funzione d’onda, otterremo sempre in
modulo il valore kh , ma metà delle misure forniranno il valore kh e metà il
valore − kh .
La stessa interpretazione si applica a qualsiasi funzione d’onda scritta
come combinazione lineare di autofunzioni di un operatore
ψ = c1ψ 1 + c 2ψ 2 + ... = ∑ c kψ k
k
dove i ck sono coefficienti numerici e le ψk corrispondono a diversi stati
del momento.
Le ψk formano un set completo di autofunzioni, nel senso che ogni
funzione può essere espressa come loro combinazione lineare. La
meccanica quantistica afferma che:
• come risultato di una singola misura, si troverà uno degli
autovalori corrispondenti alle ψk;
• la probabilità di ottenere, in una determinata misura, l’autovalore
2
corrispondente a ψk è proporzionale a c k ;
• il valore medio su un grande numero di misure è dato dal valore di
aspettazione Ω dell’operatore Ω̂ , definito come
Ω = ∫ψ *Ωˆ ψdτ
5.3 Il principio di indeterminazione
Abbiamo visto che se conosciamo esattamente il momento di una
particella non possiamo determinarne la posizione e viceversa.
⇓
E’ impossibile specificare simultaneamente, con precisione arbitraria,
posizione e momento di una particella (Heisenberg, 1925).
Le grandezze momento e posizione si dicono complementari e sono
legate dalla relazione
1
2
∆p∆q ≥ h
dove ∆p e ∆q sono le incertezze, definite come
(
)
1/ 2
∆p = p 2 − p 2
(
)
1/ 2
∆q = q 2 − q 2
Il principio di indeterminazione ha validità più generale e si applica
ad altre coppie di grandezze complementari (es.: tempo ed energia). In
particolare, due osservabili Ω1 e Ω2 si dicono complementari se vale la
relazione
Ωˆ 1 (Ωˆ 2ψ ) ≠ Ωˆ 2 (Ωˆ 1ψ )
In questo caso si dice che i due operatori non commutano.
I risultati della applicazione di due operatori in ordine differente
vengono espressi introducendo il commutatore di due operatori, definito
come
[Ωˆ 1, Ωˆ 2 ] = Ωˆ 1Ωˆ 2 − Ωˆ 2 Ωˆ 1
In particolare, il commutatore degli operatori momento e posizione vale:
[xˆ, pˆ x ] = ih
Il concetto di commutatore è di così vitale importanza in meccanica
quantistica, che è preso come elemento fondamentale di distinzione tra
l’approccio classico e quello quantistico.
Nel caso generale di due osservabili Ω1 e Ω2, il principio di
indeterminazione di Heisenberg assume la forma
∆Ω1∆Ω 2 ≤
[
1 ˆ ˆ
Ω1 , Ω 2
2
]