1 Scritto di Algoritmi e s.d. (1o anno) 14 Settembre 2004 Testo e

Scritto di Algoritmi e s.d. (1o anno)
14 Settembre 2004
Testo e RISPOSTE (in fondo)
Esercizio 1 (punti 6 in prima approssimazione)
Consideriamo il seguente codice C:
typedef
struct
struct nodo * Alb;
nodo { int info;
Alb sin, des; };
Alb semplifica (Alb t) {
Alb aux ;
if (t != NULL) {
if ( (t->sin != NULL) && (t->des != NULL) ) {
t->sin = semplifica(t->sin) ;
t->des = semplifica(t->des) ;
}
if ( (t->sin != NULL) && (t->des == NULL) ) {
aux = t;
t = semplifica(t->sin) ;
free(aux);
}
if ( (t->sin == NULL) && (t->des != NULL) ) {
aux = t;
t = semplifica(t->des) ;
free(aux);
}
}
return(t);
}
Domanda:
qual'è l'effetto della chiamata
tt = semplifica(tt)
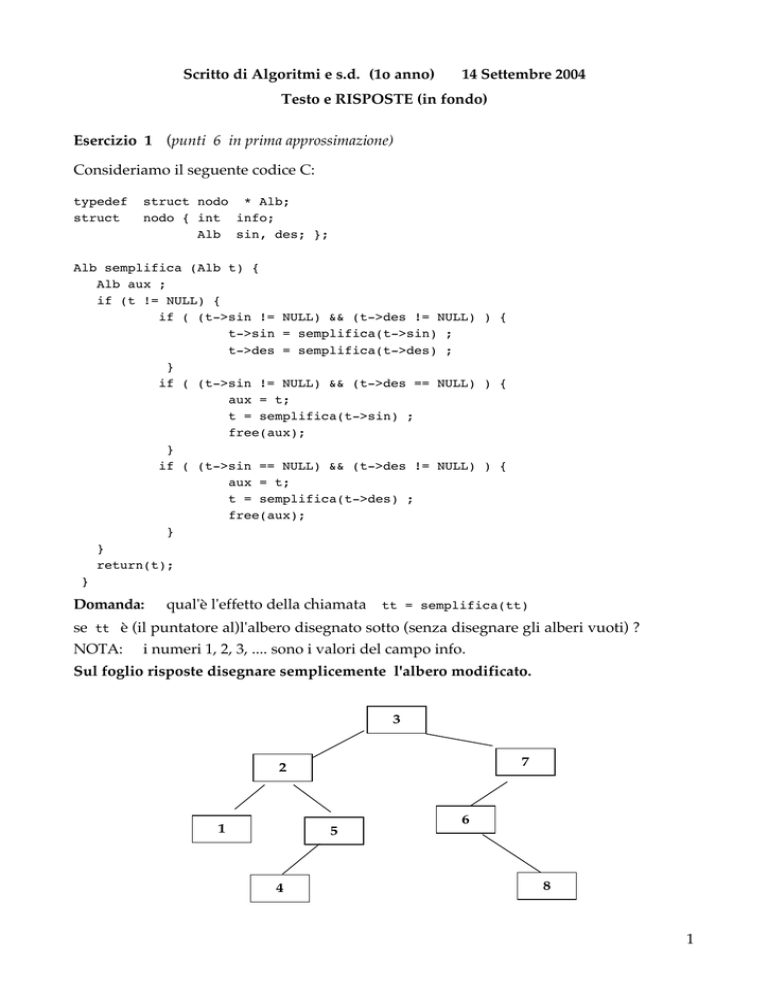
se tt è (il puntatore al)l'albero disegnato sotto (senza disegnare gli alberi vuoti) ?
NOTA: i numeri 1, 2, 3, .... sono i valori del campo info.
Sul foglio risposte disegnare semplicemente l'albero modificato.
3
7
2
1
5
4
6
8
1
Esercizio 2 (punti 10 in prima approssimazione)
Consideriamo il tipo di dato dizionario di stringhe, con le seguenti caratteristiche:
• un dizionario è un insieme finito di stringhe
• le stringhe sono successioni di lunghezza arbitraria di lettere (le 26 lettere minuscole
dell'alfabeto inglese)
e con le solite operazioni:
• empty
dizionario vuoto
• is-empty
is-empty(d) =
"d è vuoto ? "
• add
add(d, s) :
aggiunge la stringa s a d, se non è già presente
• del
del(d, s) :
cancella s da d, se presente
• member
member(d, s) =
vero se d contiene s, falso altrimenti
Per questi dizionari, consideriamo un'implementazione basata su un tipo di albero detto
trie; vediamo qualche esempio; ulteriori speigazioni alla lavagna.
Il dizionario vuoto si rappresenta con l'albero vuoto.
Il dizionario {abc, ad, ca, cane, casa} si rappresenta con l'albero che segue
a
c
b
d
a
c
n
e
s
a
Notare che i nodi "neri" indicano la fine di una parola contenuta nel dizionario; quindi:
abc è nel dizionario, mentre né a né ab ne fanno parte; ca, cane, casa sono nel dizionario,
mentre c, can, cas non ci stanno.
A questo punto:
inserire nel dizionario la stringa zucca, comporta la creazione di un intero ramo nuovo
nell'albero, mentre per aggiungere la stringa callo dobbiamo seguire il cammino, già
presente, ca e poi aggiungere il pezzo relativo a llo.
2
Domande
a)
(2 punti)
precisare quali sono le sorti di questo tipo di dato (scegliere dei nomi ragionevoli),
e, per ciascuna sorte, l'insieme corrispondente
sorte
b)
insieme
b1)
(8 punti)
Descrivere una implementazione del tdd, basata sull'idea di trie, precisando:
i tipi usati (in C o pseudocodice);
b2)
come è implementato il trie vuoto;
b3)
come viene rappresentato il trie disegnato sopra;
b4)
l'implementazione dell'operazione
add
Esercizio 3 (punti 8 in prima approssimazione)
Si tratta di trasformare alberi implementati nel modo solito in alberi rappresentati con la
tecnica figlio sinistro - fratello destro (vedere oltre per disegno). Per semplicità,
consideriamo il caso di alberi ordinati, con apertura dei nodi al piú 2, senza albero vuoto,
con etichette intere.
Per fissare le idee, i tipi sono:
Alb2 = puntatore a Nodo2
Nodo2 = record
info : integer;
primo, secondo : Alb2
end
AlbFF = puntatore a NodoFF
NodoFF = record
info : integer;
figlio, fratello : AlbFF
end
Vogliamo una procedura/funzione che preso un albero tt di tipo Alb2 produce un albero
ff di tipo AlbFF, che rappresenta tt nello stile figlio sinistro - fratello destro.
3
Domande.
a)
Usando i tipi di sopra, eventualmente tradotti in C (ma senza cambiare i nomi !!!)
scrivere, in pseudocodice, o in C (ma senza mescolare), la procedura/funzione,
commentando dove necessario.
b)
Precisare come si chiama la procedura/funzione a partire dal "main".
Rappresentazione stile figlio sinistro, fratello destro, come sulle dispense.
L'albero:
A
D
B
C
G
E
F
H
I
viene rappresentato con la struttura seguente:
A
B
C
D
E
F
G
H
I
4
Esercizio 4 (punti 6 in prima approssimazione)
Consideriamo il seguente (pezzo di) algoritmo, che non fa nulla di interessante ....:
variabili:
dim : integer
VARIANTI : max, sup, num
istruzioni:
leggi (dim)
{
}
blocco con dichiarazioni ....
variabili :
aaa : array [ 1 .. dim ; 1 .. dim ] of integer
righe, col , k: integer
istruzioni:
per righe = 1, 2, ..., dim :
per col = 1, 2, ...., dim : aaa[ righe, col ] <---- 0
col <--- dim
per righe = 1, 2,..., dim : {
k <---- col
while k>0
do { aaa[righe, k] <---- 1 ; k <---- k -1 }
col <--- col div 2 (divisione intera)
}
chiude blocco
Domanda:
Calcolare la complessità dell'algoritmo, nel caso peggiore, in funzione di
dim.
Possibilmente dare la stima in Θ( ... ). Non fare conti troppo dettagliati (esplicitando
tutte le costanti,....), ma non limitarsi nemmeno a dare il risultato, o a quattro
chiacchere.
RISPOSTE
Esercizio 1 (qui le etichette non erano uguali per tutti i compiti.....)
3
8
2
1
4
5
Esercizio 2
sorte
insieme
bool
BOOL ={vero, falso}
str
STR ={a,b,c,...., z}*
diz
DIZ = insieme dei sottinsiemi finiti di STR
è anche ragionevole considerare:
lett
b1)
LETT = {a,b,c,...., z}
dunque STR = LETT*
Qui cerco di mettere "tutti i dettagli"; ovviamente non mi aspettavo che nello
scritto ci fosse questo livello di dettaglio
tipi usati (in pseudocodice)
const NUM = 25
Stringa = puntatore a carattere (stile C),
così non si deve fissare la lunghezza
poi le tratto come array .....
suppongo che si usi il terminatore '\0' come in C
Trie = puntatore a NodoTrie
NodoTrie = record
nero : booleano
figli: array [0..NUM] of Trie
end
L'idea è che i 26 puntatori corrispondono ad a, b, c,...;
mentre il campo nero corrisponde al "colore" del nodo.
Nota
come alternativa si poteva usare solo un array di 26+1 puntatori; l'ultimo puntatore: se
è nullo indica nodo "bianco" se è non nullo, indica "nodo nero";
oppure, usare una lista linkata, invece dell'array (e allora nella lista compaiono solo le
lettere effettivamente usate ....)
b2)
trie vuoto : puntatore nullo
(alternativa : nodo con tutti i puntatori nulli e campo "nero" = falso)
b3)
qui sarebbe comodo fare il disegno a mano .... non lo faccio tutto ...
le freccette stitiche sono puntatori non nulli .........
6
questo è il nodo radice
falso
|
|
v
v
questo nodo e` collegato alla
radice dal puntatore di indice 2,
che corrisponde a 'c'
falso
.....
.....
|
v
questo nodo e` collegato al
precedente col puntatore di indice
0, cioe 'a'
vero
.............
.....
| ............
| .....
v
v
I due puntatori di sopra sono quelli che corrispondono an 'n' (indice : 'n'-'a') ed
's' (indice : 's'-'a');
il disegno è molto incompleto .....
b4)
implementazione dell'operazione add
Uso una funzione principale (add) ed una procedura usiliaria (addaux), ricorsiva
function add (d : Trie, s: Stringa) : Trie
{
var j: intero
if d = NULL then {
new(d)
d->nero <--- falso
per j = 0, 1, ... NUM : (d->figli)[ j ] <--- NULL
}
addaux (d, s, 0)
vedere oltre
return (d)
}
7
La procedura addaux si aspetta un d che non e` nullo; k indica la posizione in s che ci
interessa
notare che s[k] - 'a' produce 0 se s[k] è a, 1 se s[k] è b,......
proc addaux (d : Trie IN-OUT, s: Stringa IN , k :integer IN ) {
var
aux : Trie;
if s[k] = '\0' then
j : intero
d->nero <---- true
else {
if (d->figli) [ s[k] - 'a' ] = NULL
then
{
new(aux) ;
aux ->nero <---- falso
per j = 0, 1, ... NUM : aux[j] <--- NULL
(d->figli) [ s[k] - 'a' ] <---- aux
}
addaux( (d->figli) [ s[k] - 'a' ] , s, k+1)
}
}
Esercizio 3
Usando una funzione, in pseudocodice:
a)
function trans (t : Alb2) : AlbFF
var aux : AlbFF
if t = NULL
then return (NULL)
anche se gli alberi vuoti non sono previsti, serve per gestire
facilmente la ricorsione .....
else
new (aux)
aux->info
<----
t->info
aux->fratello <---- NULL
if t->primo = NULL
la radice ha fratello nullo
se non ci sono figli ...
then aux->figlio <---- NULL
else {
aux->figlio <---- trans(t->primo)
(aux->figlio)->fratello
<---- trans(t->secondo)
}
return (aux)
Nota:
aux->figlio <---- trans(t->primo)
si crea un albero nuovo,
e lo si inserisce come figlio sinistro nel nodo puntato da aux; la radice
di questo albero ha un campo fratello che e` nullo;
con l'istruzione
trans(t->primo) ,
con l'istruzione
(aux->figlio)->fratello
<---- trans(t->secondo)
si fa puntare il campo fratello all'albero prodotto da trans(t->secondo)
8
parte b) la chiamata è
Esercizio 4
ff <---- trans(tt) dove tt ed ff sono variabili ......
(Variante dove si usa "dim" )
L'algoritmo è in Θ( dim 2 ); infatti:
• tutto è a costo costante tranne i due "per" annidati ed il secondo "per", con dentro un
while;
• ovviamente,
per righe = 1,..., dim : per col =1, ...., dim : ....
ha un costo della forma
• l'istruzione
a dim*dim +b dim +c (con a,b, c costanti e a >0)
per righe = 1,..., dim { .. while ..}
ha un costo della forma:
(W_1 + d) + (W_2 + d) + .... (W_n + d) + d'
dove d e d' sono costanti e W_j è il costo dell'istruzione while quando righe = j;
Il costo massimo è W_1; in questo caso il while ha un costo lineare in dim;
quindi, W_j ha un costo al piú lineare in dim
quindi tutta l'istruzione "per" ha un costo al piú quadratico in dim;
dunque domina il doppio "per" iniziale.
Non ci sono casi peggiori (perchè stiamo misurando la complessità in funzione di dim
che è l'input, non la dimensione dell'input ....).
=================
Volendo fare i conti precisi (e supponendo che dim sia potenza di 2):
W_1
= p * dim + q
W_2
= p* dim/2 +q
W_3
= p* dim/4 + q
......................................
poichè 1 + 1/2 + 1/4 + .... <= 2
si ha che l'istruzione : per righe = 1,..., dim { .. while ..}
ha in effetti un costo lineare in dim.
9