Prova scritta di Misure Elettriche NO del 3_luglio_2013
1. Un voltmetro integratore a doppia rampa, con risoluzione di 5 cifre e mezza e dinamica da 0V a 39.9999V, opera con
un orologio interno alla frequenza di 10MHz. Lo strumento è stato progettato per avere un tempo di salita pari a
100ms. Dopo aver disegnato lo schema a blocchi e chiarito il suo funzionamento, la sua risoluzione, le incertezze
coinvolte e la loro minimizzazione, calcolare il valore della tensione di riferimento utilizzata. Quanto vale il tempo
di misura, almeno indicativamente?
2. Mediante un oscilloscopio numerico a quattro canali, banda 100 MHz e 8 bit di risoluzione, si vogliono osservare
contemporaneamente un'onda sinusoidale con frequenza 5 MHz ed uno con frequenza 10 MHz, in fase tra loro. Il
primo ha un ampiezza di picco pari a 1 V mentre quella del secondo è di 100 mV. E' adatto lo strumento? Se lo
schermo ha 10 divisioni orizzontali e 8 verticali indicare tutte le impostazioni dello strumento per una
visualizzazione a pieno schermo di 1 periodo di entrambi i segnali. Rappresentare graficamente cosa verrà
visualizzato. Se l'accuratezza è pari al 2% del fondo scala esprimere la misura del valore di picco, della frequenza e
del periodo. Trovare anche valore efficace e valor medio raddrizzato. Infine descrivere il tipo di campionamento che
converrà adottare in questo caso.
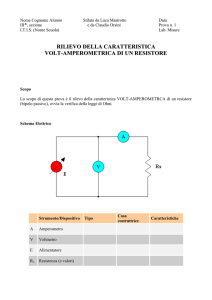
3. Un voltmetro con resistenza interna di 100 k ± 1% viene utilizzato per misurare una sorgente di tensione di valore
10 V ± 1% e con resistenza interna 2 k ± 1%. Qual è la tensione realmente misurata sul voltmetro? Fornire una
classificazione degli strumenti di misura e controllo.
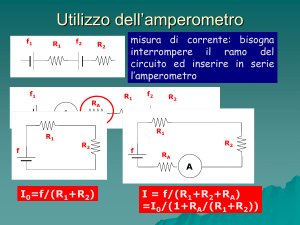
4. Un amperometro elettromeccanico a bobina mobile presenta una resistenza interna di 100 ± 1% e viene utilizzato
per misurare la corrente erogata da una sorgente di tensione di valore 10 V ± 1% e con resistenza interna 2 k ± 1%.
Qual è la corrente realmente misurata sull’amperometro? Disegnare lo schema circuitale e chiarire il funzionamento
di tale strumento anche come voltmetro e ohmetro.
1. (9 punti) Il direttore di un giornale intende determinare la proporzione di giornali stampati che non sono idonei alla
vendita. Viene estratto allora un campione di 200 giornali e si osserva che 35 di essi non sono idonei. Calcolate
l'intervallo di confidenza del 90% per la proporzione di giornali non idonei nella popolazione.
Supponiamo poi che, in un secondo tempo, il direttore, non disponendo di alcuna informazione riguardante p,
intenda determinare l'ampiezza del campione necessaria per assicurare un errore campionario non superiore a 0.05.
Determinare l'ampiezza di tale campione. Stime puntuali e loro principali proprietà.
2. (9 punti) Date due popolazioni normali indipendenti, supponiamo di estrarre dalla prima un campione di ampiezza
n1=8 e dalla seconda un campione di ampiezza n2=10 e di osservare le seguenti varianze campionarie:
S12 56 S 22 24 . Dopo aver determinato i due valori critici inferiore e superiore, si verifichi al livello di
significatività =0.05 e =0.01 l'ipotesi di uguaglianza delle varianze. Interpretare e commentare anche
graficamente l'esercizio. E’ possibile determinare il p-value? In ogni caso spiegare di cosa si tratta anche in
relazione all’errore di secondo tipo.
3. (12 punti) Nel questionario consegnato ai clienti di 3 diversi alberghi di una stessa catena, diciamo A, B e C, i motivi
di insoddisfazione dovuti al prezzo sono stati rispettivamente (23, 7, 37), quelli dovuti alla posizione dell'albergo
sono stati rispettivamente (39, 13, 8), quelli relativi alle camere sono stati rispettivamente (13, 5, 13) altri motivi
sono stati rispettivamente (13, 8, 13). Determinare se sussiste una relazione tra il particolare albergo visitato e il
motivo prevalente di insoddisfazione. Commentare e illustrare anche graficamente il problema.