Prova scritta di Misure Elettriche MECC 5 novembre 2014

Prova scritta di Misure Elettriche MECC del 5 novembre 2014
1. Nella misura di una resistenza incognita con metodo potenziometrico, che va innanzitutto schematizzato e descritto, si
hanno le seguenti cinque letture di tensione e di corrente:
Lettura
Tensione (V)
Lettura
Corrente (mA)
1.
2.
3.
4.
5.
9.47
9.45
9.31
9.36
9.56
1.
2.
3.
4.
5.
30.4
29.7
30.0
29.8
30.3
L’accuratezza di entrambi gli strumenti è pari a 3 counts. Si consideri di poter usare una qualsiasi configurazione con
voltmetro a monte o a valle, trascurando le eventuali conseguenze, purchè si tenga conto del coefficiente di
correlazione tra le letture in tabella. Valutare la misura della resistenza con incertezza assoluta e relativa.
2. Dopo aver schematizzato una classificazione degli strumenti per misura e controllo, parlare delle unità non SI in uso
e di come è organizzata la metrologia a livello nazionale e internazionale.
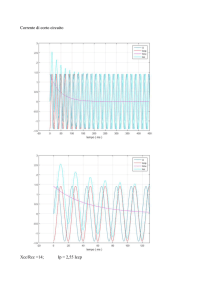
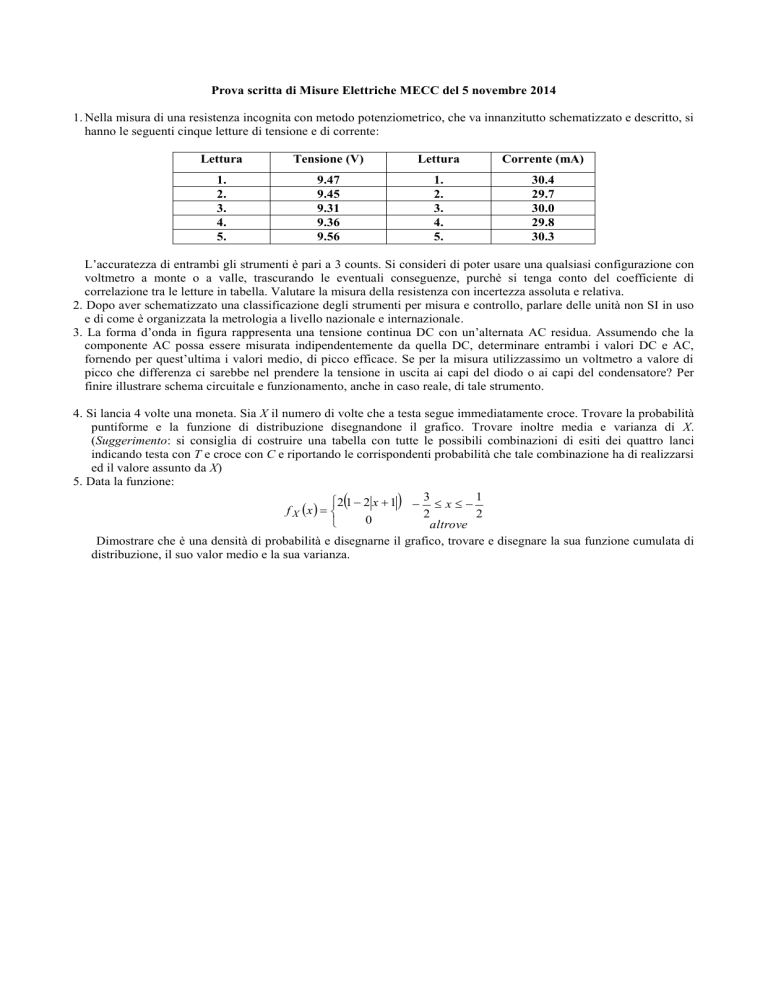
3. La forma d’onda in figura rappresenta una tensione continua DC con un’alternata AC residua. Assumendo che la
componente AC possa essere misurata indipendentemente da quella DC, determinare entrambi i valori DC e AC,
fornendo per quest’ultima i valori medio, di picco efficace. Se per la misura utilizzassimo un voltmetro a valore di
picco che differenza ci sarebbe nel prendere la tensione in uscita ai capi del diodo o ai capi del condensatore? Per
finire illustrare schema circuitale e funzionamento, anche in caso reale, di tale strumento.
4. Si lancia 4 volte una moneta. Sia X il numero di volte che a testa segue immediatamente croce. Trovare la probabilità
puntiforme e la funzione di distribuzione disegnandone il grafico. Trovare inoltre media e varianza di X.
(Suggerimento: si consiglia di costruire una tabella con tutte le possibili combinazioni di esiti dei quattro lanci
indicando testa con T e croce con C e riportando le corrispondenti probabilità che tale combinazione ha di realizzarsi
ed il valore assunto da X)
5. Data la funzione:
21  2 x  1   3  x   1
f X x   
2
2
0

altrove
Dimostrare che è una densità di probabilità e disegnarne il grafico, trovare e disegnare la sua funzione cumulata di
distribuzione, il suo valor medio e la sua varianza.