Esercizi svolti
Resistori in serie e in parallelo
Esercizio n° 1
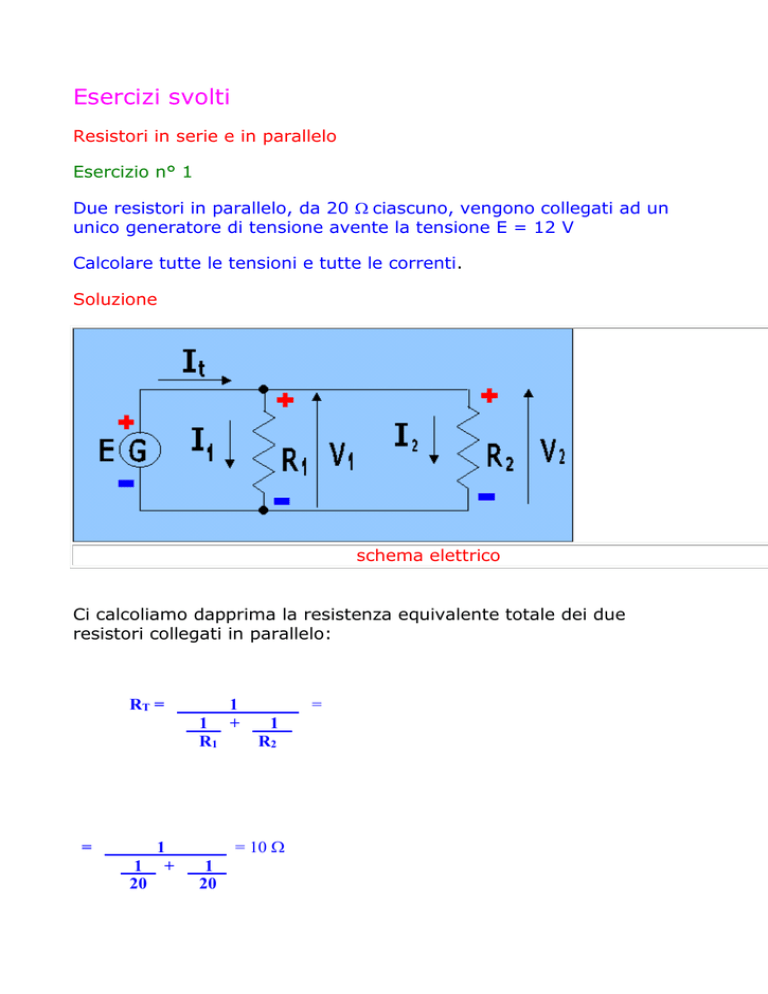
Due resistori in parallelo, da 20 ciascuno, vengono collegati ad un
unico generatore di tensione avente la tensione E = 12 V
Calcolare tutte le tensioni e tutte le correnti.
Soluzione
schema elettrico
Ci calcoliamo dapprima la resistenza equivalente totale dei due
resistori collegati in parallelo:
RT =
1
R1
=
1
1 +
20
1
+
=
1 .
R2 .
. = 10
1 .
20 .
Con la legge di Ohm ci calcoliamo la corrente totale del circuito:
Vt = Rt x It
Ricaviamo la formula inversa:
It =
Vt
Rt
= 12
10
= 1,20 A
Essendo tutti i componenti collegati parallelo avranno tutti la stessa
tensione; quindi:
V1 = V2 = E = 12,00 V
Non resta ora che calcolare le due correnti dei due resistori:
I1 =
V1
R1
= 12
20
= 0,60 A
I2 =
V2
R2
= 12
20
= 0,60 A
Esercizio n° 2
Calcolare tutte le tensioni e tutte le correnti del seguente circuito.
E = 12 V
R1 = 1
R2 = 1.000
R3 = 1.000
schema elettrico
dati conosciuti
Notiamo che i resistori R2 ed R3 sono collegati in parallelo, in quanto
tutti e due hanno i rispettivi terminali l'uno collegato al punto A e
l'altro al punto B del circuito
Poiché i due resistori R2 ed R3 sono in parallelo ci calcoliamo la loro
resistenza equivalente Rp:
Rp =
1
R2
=
1
+
=
1
R3 .
.
= 500
1
1 +
1 .
1000
1000 .
Sostituendo ai due resistori R1 ed R2 il loro parallelo Rp, il circuito
diventa:
Circuito equivalente a quello iniziale
Ci calcoliamo, ora la resistenza totale; notiamo che R1 ed Rp sono in
serie, quindi la loro resistenza equivale alla seguente:
Rt = R1 + Rp = 1 + 500 = 501
Il circuito, ora è il seguente:
Circuito equivalente a quello iniziale
Con la legge di Ohm ci calcoliamo la corrente totale del circuito.
Vt = Rt x It
Ricaviamo la formula inversa:
It
Vt = 12
Rt
501
= 0,023952 A
La corrente totale circola nella resistenza totale Rt .
Riconsideriamo, ora, il circuito equivalente precedente:
Circuito equivalente a quello iniziale
La corrente sarà uguale in tutti i componenti del circuito e in
particolare in R1 e in Rp. Quindi possiamo scrivere:
I1 = Ip = It = 0,023952 A
A questo punto ci possiamo calcolare le due tensioni esistenti ai capi
di R1 e ai capi del parallelo Rp, utilizzando la legge di Ohm. Otteniamo,
allora:
V1 = R1 x I1= 1 x 0,023952 = 0,023952 V
mentre per Vp otteniamo:
Vp = Rp x Ip= 500 x 0,023952 = 11,976 V
Ma poiché Rp rappresenta il parallelo dei due resistori R2 ed R3, e
sapendo che i resistori in parallelo hanno la stessa tensione, possiamo
scrivere:
V2 =V3 =Vp = 11,976 V
Applicando ora la formula inversa della legge di Ohm ci possiamo
calcolare le due correnti:
I2 =
V2 = 11,976 = 0,011976 A
R2
Analogamente per I3 otteniamo:
I3 =
V3
R3
= 11,976 = 0,011976 A
Esercizio n° 3
Calcolare tutte le tensioni e tutte le correnti del seguente circuito.
Soluzione
E=1
R1 =
R2 =
R3 =
R4 =
schema elettrico
Notiamo che i resistori R3 ed R4 sono collegati in parallelo, in quanto
tutti e due sono collegati agli stessi punti.
Poiché i due resistori R2 ed R3 sono in parallelo ci calcoliamo la loro
resistenza equivalente Rp:
Rp =
1
R3
=
1
+
1
R4 .
.
= 96
1
1
192
=
+
1 .
192 .
Sostituendo ai due resistori R3 ed R4 il loro parallelo Rp, il circuito
diventa:
da
conos
circuito equivalente a quello iniziale
Notiamo, ora, che i tre resistori sono collegati in serie e quindi ci
calcoliamo la resistenza equivalente dei tre resistori collegati in serie:
RT = R1 + R2 + Rp = 2 + 2 + 96 = 100
Il circuito diventa:
Circuito equivalente a quello iniziale
Con la legge di Ohm ci calcoliamo la corrente totale del circuito.
Vt = Rt x It
Ricaviamo la formula inversa e ci calcoliamo la corrente totale:
It =
Vt
Rt
= 12
100
= 0,12 A
Ritornando, ora, al circuito equivalente con i tre resistori in serie:
circuito equivalente a quello iniziale
Essendo tutti i componenti collegati in serie avranno tutti la stessa
corrente; quindi:
I1 = I2 = Ip = It = 0,12 A
Non resta ora che calcolare le tre tensioni dei tre resistori:
V1 = R1 x I1= 2 x 0,12 = 0,24 V
Analogamente per R2 otteniamo:
V2 = R2 x I2= 2 x 0,12 = 0,24 V
Analogamente per Rp otteniamo:
Vp = Rp x Ip= 96 x 0,12 = 11,52 V
schema elettrico iniziale
Ma poichè Rp rappresenta il parallelo tra R3 ed R4, vuol dire che sia R3
che R4 avranno la stessa tensione del parallelo, e cioè otteniamo:
V3 = V4 = Vp = 11,52 V
Non resta ora che calcolare le due correnti dei due resistori in
parallelo:
I3 =
V3
R3
= 11,52 = 0,06 A
192
I4 =
V4
R4
= 11,52
192
= 0,06 A
Esercizi da svolgere
Esercizio n° 1
Due resistori in parallelo, da 20 ciascuno, vengono collegati ad un
unico generatore di tensione tensione avente la tensione E = 220 V
Calcolare tutte le tensioni e tutte le correnti.
Esercizio n° 2
Calcolare tutte le tensioni e tutte le correnti del seguente circuito:
E = 220
V
R1 = 50
R2 = 50
Rp = 900
dati
conosciut
Circuito elettrico
Esercizio n° 3
Calcolare tutte le tensioni e tutte le correnti del seguente circuito:
E=2
V
R1 =
R2 =
R3 =
1.600
R4 =
1.600
da
conos
schema elettrico
Prof. Pietro De Paolis
Elettrotecnica per istituti tecnici
Economia generale
Elettrotecnica ed elettronica per professionali
Prima classe scuola primaria
Guida scolastica
Scuola Elettrica
2005