Solo quello che ti interessa | Geometrie non euclidee - Modelli di geometria iperbolica
Copyright admin [email protected]
http://www.belloma.it/geometrie-non-euclidee-modelli-di-geometria-iperbolica/
Geometrie non euclidee - Modelli di geometria
iperbolica
- Il modello per la geometria euclidea è il piano. Vediamo come individuare una
modello si superficie per la geometria iperbolica.
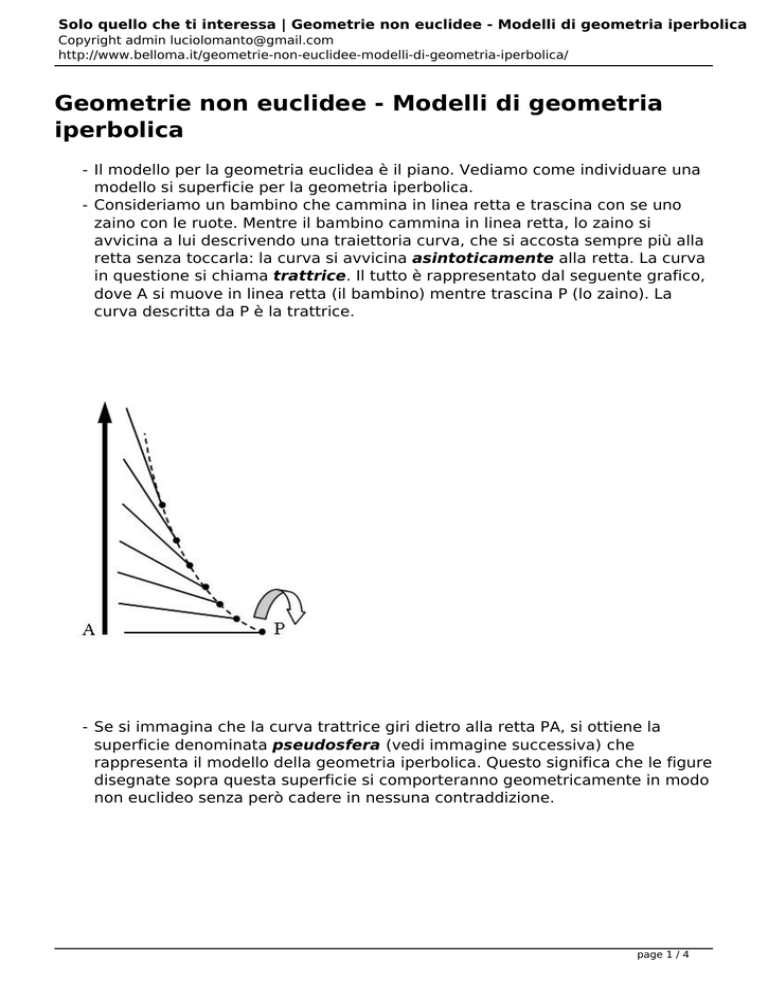
- Consideriamo un bambino che cammina in linea retta e trascina con se uno
zaino con le ruote. Mentre il bambino cammina in linea retta, lo zaino si
avvicina a lui descrivendo una traiettoria curva, che si accosta sempre più alla
retta senza toccarla: la curva si avvicina asintoticamente alla retta. La curva
in questione si chiama trattrice. Il tutto è rappresentato dal seguente grafico,
dove A si muove in linea retta (il bambino) mentre trascina P (lo zaino). La
curva descritta da P è la trattrice.
- Se si immagina che la curva trattrice giri dietro alla retta PA, si ottiene la
superficie denominata pseudosfera (vedi immagine successiva) che
rappresenta il modello della geometria iperbolica. Questo significa che le figure
disegnate sopra questa superficie si comporteranno geometricamente in modo
non euclideo senza però cadere in nessuna contraddizione.
page 1 / 4
Solo quello che ti interessa | Geometrie non euclidee - Modelli di geometria iperbolica
Copyright admin [email protected]
http://www.belloma.it/geometrie-non-euclidee-modelli-di-geometria-iperbolica/
- Gli assiomi della geometria di Lobachevski nascono quando si studia il
comportamento di punti e rette sopra questa superficie.
- Lobachevski propose come alternativa al quinto postulato che, data una retta
r ed un punto P non appartenente ad r, possono essere tracciate per P infinite
rette parallele ad r.
- Su questa superficie le rette parallele non sono equidistanti e la somma
degli angoli A, B e C è minore di 180°, a differenza della geometria euclidea.
- Le rette sopra questa superficie sono le linee più brevi tra i punti di essa:
queste linee sono denominate linee geodetiche. Dal punto di vista euclideo,
queste rette sembrano curve (a chi è fuori dalla superficie). Nell’esempio sono
state evidenziate alcune di queste.
Modelli reali e non di superfici iperboliche - Un esempio, citato da Albert Einstain per definire lo spazio-tempo, è quella
della superficie di un lenzuolo sul letto in cui possiamo un peso al centro: si
creerà così una superficie curva con andamento iperbolico, dai lati del letto al
punto in cui abbiamo messo l’oggetto pesante: si può osservare che la
superficie smette di essere piana in prossimità del peso.
- Un’altra superficie è rappresentata dalla sella dei cavalli. Qui le linee parallele
non rimangono a distanza costante, ma divergono progressivamente tra loro.
- Un altro esempio è la campana di una tromba. Se si immaginano due abitanti
sulla superficie della tromba che si muovano verso la campana è evidente che
dall’interno, entrambi gli abitanti si muoveranno in modo rettilineo, ma
page 2 / 4
Solo quello che ti interessa | Geometrie non euclidee - Modelli di geometria iperbolica
Copyright admin [email protected]
http://www.belloma.it/geometrie-non-euclidee-modelli-di-geometria-iperbolica/
dall’esterno le due linee percorse saranno divergenti (quindi curve). Le due
linee tracciate saranno comunque sempre parallele.
- Nel 1870 il matematico tedesco Felix Klein (1849-1925) introdusse un
modello di geometria iperbolica sul piano, ampliandolo nello spazio.
- In questo modello viene considerata la circonferenza euclidea e una
nuove definizioni di piano, punto e rette.
- Klein dimostrò che la geometria costruita sopra il cerchio, con le
definizioni sotto elencate, equivale alla geometria iperbolica,
soddisfacendo gli assiomi di Euclide, ad esclusione del quindi postulato, e
rispettando i risultati della geometria iperbolica. - Il piano è rappresentato dalla superficie interna al cerchio.
- I punti sono tutti i punti interni a questo piano, circonferenza
esclusa.
- Le rette sono le corde interne al cerchio, escludendo gli estremi
sulla circonferenza.
- Le rette parallele sono corde con non si incontrano in nessun
punto del piano
- Le rette secanti sono corde che si incontrano all’interno del cerchio
- In questo modello avremo infinite rette parallele passanti per un punto P
esterno ad una retta data. Nell’esempio le rette r, s e t sono parallele a l
visto che non si incontrano in nessun punto:
- Nell'opera di Maurits Cornelis Escher (1898-1972), denominata Paradiso
ed Inferno, gli elementi (angeli e demoni) si riducono di dimensioni man
mano che si avvicinano al cerchio, e sembra che continuino all’infinito. Escher
page 3 / 4
Solo quello che ti interessa | Geometrie non euclidee - Modelli di geometria iperbolica
Copyright admin [email protected]
http://www.belloma.it/geometrie-non-euclidee-modelli-di-geometria-iperbolica/
creò questo disegno per rappresentare una superficie impossibile in due
dimensioni: le proprietà di questo spazio piano ci trasportano alla geometria
non euclidea di tipo iperbolico
page 4 / 4









