Document

SOSTANZA PURA
Un sistema si dice costituito da una sostanza pura se in esso è presente una
sostanza di composizione chimica fissata: essa può presentarsi in differenti stati
di aggregazione fisica ovvero solido, liquido, aeriforme.
Ciascuno degli stati di aggregazione è detto FASE.
FASE
Con riferimento ad una sostanza pura, la fase è l’insieme di tutte le parti omogenee
del sistema aventi lo stesso stato intensivo.
Sebbene pressione e temperatura siano uniformi in un sistema a più fasi, tutte le
proprietà specifiche cambiano con discontinuità attraversando il confine che
limita due qualsiasi delle fasi presenti.
SISTEMA SEMPLICE
Il sistema semplice è costituito da una sostanza pura il cui stato intensivo sia
individuato da due proprietà interne intensive indipendenti.
Il sistema semplice comprimibile o sistema p,v,T è detto così quando il suo stato
intensivo è descrivibile con le proprietà pressione, volume specifico e temperatura,
due delle quali saranno considerate indipendenti.
REGOLA DELLE FASI O DI GIBBS
Per una sostanza pura (ad un solo componente) vale la seguente regola:
V=3-F
dove con F si è indicato il numero delle fasi coesistenti in equilibrio e con V, detta
varianza, il numero delle possibili variazioni, tra p e T, tali che F non cambi.
SISTEMA COSTITUITO DA UN’UNICA FASE E’ BIVARIANTE
V=3-1=2 ovvero è possibile variare pressione e temperatura senza mutare il numero
di fasi presenti.
SISTEMA COSTITUITO DA DUE FASI E’ MONOVARIANTE
V=3-2=1 ovvero è possibile variare solo una tra pressione e temperatura affinchè due
fasi coesistano in equilibrio.
SISTEMA INVARIANTE O SISTEMA AL PUNTO TRIPLO.
V=3-3=0 ovvero in tale sistema sono presenti in equilibrio tre fasi, per cui una
qualunque variazione di p o di T comporterebbe la scomparsa di almeno una
fase.
Il punto triplo è dunque per definizione quel punto di coesistenza di tutte e tre gli
stati di aggregazione in cui il sistema è invariante.
POSTULATO
Per un sistema p,v,T ad un solo componente, gli stati di equilibrio possono
essere rappresentati da una superficie detta caratteristica in uno spazio a tre
dimensioni.
f ( v , p, T ) = 0
Per una sostanza pura
che possiede una sola
fase solida
e che è caratterizzata da
un volume specifico del
liquido maggiore
di quello del solido. Ciò
si verifica in quasi tutte
le sostanze pure
ad eccezione dell’acqua
che solidificando
espande.
Esaminiamo il comportamento di una sostanza pura
Si consideri una massa unitaria di sostanza pura in fase solida contenuta in un
sistema pistone cilindro.
Si supponga che la trasformazione sia internamente reversibile.
Essendo la trasformazione isobara, dalla prima legge segue che il calore
ceduto al sistema è pari all’incremento di entalpia.
dh = δq + (pdv − δl) +vdp
dh = δq
L’incremento di entalpia si manifesta con un aumento della temperatura e del
volume: avviene una piccola dilatazione dovuta al riscaldamento.
Se si continua a somministrare calore, ha inizio il processo di FUSIONE (il
processo inverso è detto di SOLIDIFICAZIONE): si manifesta la fase liquida e
contemporaneamente si nota che la temperatura resta costante.
Il sistema in queste condizioni è detto BIFASICO.
All’interno del sistema bifasico pressione e temperatura restano uniformi, ma
le altre proprietà specifiche presentano discontinuità passando da una fase
all’altra.
Se si continua a somministrare calore, la massa della fase liquida continua ad
aumentare fino alla completa scomparsa della massa in fase solida.
La quantità di calore necessaria al completo cambiamento di fase solida in
liquida è una misura dell’ENTALPIA DI FUSIONE che può essere vista come
somma della variazione di energia interna e del lavoro di variazione di volume
scambiato con l’ambiente.
Cosa accade se si continua a somministrare calore?
Si passerà dalla fase liquida alla fase gassosa attraverso il processo di
EVAPORAZIONE ( il processo inverso è detto LIQUEFAZIONE)che vede la
coesistenza delle due fasi, liquida e gassosa.
Anche durante tale processo p e T sono costanti.
Se si continua a somministrare calore, la massa della fase gassosa continua
ad aumentare fino alla completa scomparsa della massa in fase liquida.
Quando la sostanza è tutta in fase gassosa il suo volume è notevolmente
maggiore di quello della fase liquida.
L’esperimento può essere ripetuto per differenti valori di pressione: si osserva
che i passaggi di fase solido-liquido, liquido-aeriforme avvengono a
temperature differenti: esiste una corrispondenza biunivoca tra pressione e
temperatura in un sistema bifasico in equilibrio.
TERMODINAMICA
DEGLI
STATI
Passaggio
di
fase
TERMODINAMICA
DEGLI
STATI
compare la
compare
la
fase
aeriforme
sistema:
sistema:
t liquida in
fase
sistema:
in1 equilibrio
con
kg
di
1ripercorriamo
kg
didicon
equilibrio
la
1
kg
sostanza
la
fase
liquida
sostanza
pura
la
sostanza
pura
fase
solida
pura
in
fase
somministriamo
intrasformazione
fase
inaeriforme
fase solida
liquida
calore
dopo aver
a
aumentato la
pressione
pressione
costante
v
TERMODINAMICA
se la pressione è
maggiore della
pressione del
punto critico non
c’è il passaggio di
fase
DEGLI
t
volume
specifico
fase liquida
se la pressione è
minore della
pressione del
punto triplo c’è il
passaggio di fase
solido-aeriforme
STATI
Acqua
Tc=373 °C
pc=22 MPa
punto critico
volume
specifico fase
aeriforme
punto triplo
Acqua
Tt=0 °C
pt=0,6 kPa
v
TERMODINAMICA
DEGLI
STATI
liquidoaeriforme
liquido
solido
aeriforme
pressione
critica
p
temperatura
critica
solidoliquido
solidoaeriforme
T
v
temperatura
pressione tripla
TERMODINAMICA
DEGLI
STATI
p
T
v
p
p
v
T
SUPERFICIE CARATTERISTICA per una sostanza pura che possiede una
sola fase solida ed è caratterizzata da un vliquido>vsolido: f(p,v,T)=0
mC = curva limite inferiore o linea
del liquido saturo
nC = curva limite superiore o linea
delvapore saturo
Un sistema plurifasico in equilibrio
è detto saturo
In corrispondenza del punto critico
si annullano le differenze tra i valori
delle proprietà specifiche relative
alle due fasi.
abcdef rappresentano gli stati termodinamici relativi al riscaldamento isobarico alla pressione pa.
ghil sono gli stati termodinamici relativi alla compressione isoterma dell’aeriforme: essendo Tg<Tc, la
compressione causa il passaggio di fase gas-liquido
Liquido sottoraffreddato o compresso: stati il cui punto
rappresentativo è alla sinistra della curva limite inferiore;
Liquido saturo: stati il cui punto rappresentativo è sulla
curva limite inferiore;
Vapore saturo:stati il cui punto rappresentativo tra la curva
limite inferiore e la curva limite superiore (stati interni alla
regione bifasica);
Vapore saturo secco: stati il cui punto rappresentativo sulla
curva limite superiore;
Vapore surriscaldato: stati il cui punto rappresentativo è tra
la curva limite superiore e l’isoterma critica;
N.B.
Nelle regioni monofasiche lo stato è univocamente determinato
dalla conoscenza di una qualsiasi coppia di coordinate tra p, v e
T in quanto sono tra loro indipendenti.
Nelle regioni bifasiche p e T sono tra loro dipendenti, per cui
fissata T, ad esempio, in corrispondenza di un solo valore di p
possono coesistere due fasi. La coppia individua il segmento
luogo degli infiniti stati di equilibrio per la miscela (settori
cilindrici con generatrice parallela all’asse dei volumi specifici).
E’ dunque necessario conoscere il valore di una terza proprietà
termodinamica per l’individuazione dello stato del sistema.
Lo stato triplo è caratterizzato da un’unica coppia di valori pT
dipendenti tra loro solo per la composizione chimica.
Per sostanza di lavoro acqua:
pT=6,11.102
TT=273,13K
a: condizione di solido;
b: condizione di liquido;
c: condizione di gas;
a-b: solido-liquido;
b-c: liquido-gas;
a-c: solido-gas
Il triangolo abc è su di un piano ortogonale all’asse delle
pressioni e lo interseca per un valore pari alla pressione
tripla della sostanza.
SUPERFICIE CARATTERISTICA per l’acqua un vliquido<vsolido: f(p,v,T)=0
Presenta una differente disposizione delle regioni bifasiche
Proiezione della superficie caratteristica sul diagramma p-T o di fase:
Le proiezioni delle regioni bifasiche sono delle linee e la loro linea in comune è rappresentata
dal punto triplo, le regioni monofasiche sono rappresentate da aree.
La superficie caratteristica è proiettata sul piano pT:
La linea comune alle tre regioni bifasiche si proietta in un solo punto
detto PUNTO TRIPLO “T”.
•
AT è la curva di SUBLIMAZIONE o CONDENSAZIONE;
•
BT è la curva di FUSIONE o SOLIDIFICAZIONE che in genere ha
pendenza positiva, con l’unica eccezione per sostanze come l’
acqua che solidificando si espandono;
•
CT è la curva di EVAPORAZIONE o CONDENSAZIONE (di
importanza applicativa).
Sebbene non sempre la conoscenza di entrambe le proprietà termodinamiche intensive,
pressione e temperatura, permettano l’individuazione dello stato termodinamico del sistema, la
loro conoscenza darà sempre la possibilità di individuarne la fase o le fasi presenti.
(d) liquido sottoraffreddato o compresso; stato raggiungibile mediante un raffreddamento
isobarico dallo stato di vapore saturo secco ( f ) o mediante una compressione isoterma dallo
stato di liquido saturo ( c )
( f ) vapore saturo secco;
( e ) liquido saturo;
( g ) vapore surriscaldato; stato raggiungibile mediante un riscaldamento isobarico dallo stato di
vapore saturo secco (f ).
TERMODINAMICA
T > Tc
DEGLI
STATI
sostanza
Tc [ °C]
metano
-82
acqua
374
gas l’aria e aria
il metano,
l’ossigeno, in
ossigeno
condizione
propano
ambiente, sono in
fase gassosa
-141
-118
97
TERMODINAMICA
DEGLI
STATI
acqua
t = 100 °C
acqua
p = 1 bar
t = 100 °C c
liquidop = 0,1 bar
Quando
la temperatura aeriforme
aeriforme
T<T
acqua
t = 100 °C
p = 10 bar
liquido
liquido
della sostanza è inferiore
alla sua temperatura
critica può presentarsi in
diverse fasi a seconda
del valore della pressione
aeriforme
liquido-aeriforme
TERMODINAMICA
DEGLI
STATI
acqua alla pressione
ambiente al livello del
mare bolle alla
temperatura di 100 °C
p = 101 kPa
acqua alla pressione
ambiente in montagna
bolle alla temperatura
di 95 °C
p = 85 kPa
acqua in una pentola
chiusa alla pressione di
2 bar bolle alla
temperatura di 120 °C
p = 200 kPa
t = 100 °C
t = 95 °C
t = 120 °C
TERMODINAMICA
DEGLI
STATI
per
ogni bolle
sostanza
L’acqua
a
pura esiste un
temperatura
legame
diversa monotono
a
crescente
tra
seconda
della
pressione e
pressione
temperatura
durante il
passaggio di fase
TERMODINAMICA
DEGLI
STATI
p
t
TERMODINAMICA
DEGLI
STATI
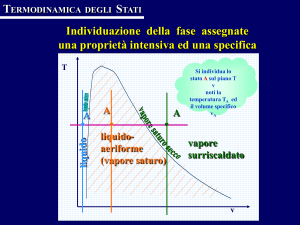
Individuazione della fase
data la pressione
assegnate due proprietà intensive
p si legge a
A
TA < Tsat(pA)
liquido sottoraffreddato
p
liquido
sottoraffreddato
A
TA > Tsat(pA)
vapore surriscaldato
TA = Tsat(pA)
vapore saturo
quale
temperatura c’è
il passaggio di
fase Tsat
pA
se la temperatura
assegnata TA è
seuguale
la temperatura
a quella di
assegnata
TA èT
saturazione
sat
minore
quellaèdi
la di
sostanza
saturazione
Tsat
vapore saturo
la sostanza è
liquido
sottoraffreddato
A
A
vapore
surriscaldato
TA
Tsat
se la temperatura
assegnata TA è
maggiore di quella
di T
saturazione
Tsat
A T
la sostanza è
vapore
surriscaldato
TERMODINAMICA
DEGLI
STATI
Individuazione della fase
assegnate due proprietà intensive
p
pA > psat(tA)
liquido sottoraffreddato
pA
A
A
psat
pA < psat(tA)
A
pA
se la pressione
assegnata pA è
maggiore di quella
di saturazione psat
la sostanza è
liquido
sottoraffreddato
vapore surriscaldato
pA = psat(tA)
vapore saturo
liquido
sottoraffreddato
data la
temperatura TA
si legge a quale
pressione c’è il
passaggio di
fase psat
se la pressione
assegnata pA è
uguale a quella di
T
saturazione psatA
la sostanza è
vapore saturo
vapore
surriscaldato
se la pressione
assegnata pA è
minore di quella
di saturazione
T psat
la sostanza è
vapore
surriscaldato
Proiezione della superficie caratteristica sul diagramma p-v:
le regioni bifasiche e quelle monofasiche si proiettano in tale piano come aree, la linea in comune
delle tre zone bifasiche è proiettata nella linea mn (degli stati tripli).
La superficie caratteristica è proiettata sul piano pv:
•
abcdef riscaldamento isobarico;
•
ghil compressione isoterma.
•
Zona di vapore saturo è quella tra le due curve limiti e dalla linea del
punto triplo (mn).
Nella zona al di sotto della campana, del vapore saturo, p e T sono tra loro dipendenti, per
cui la loro conoscenza consente di individuare su tale piano un segmento (de)
corrispondente ad infiniti stati aventi eguale p e T, ma differenti proprietà specifiche.
Proiezione della superficie caratteristica sul diagramma p-v:
La conoscenza di v e p(e quindi della T corrispondente) identifica lo stato di un vapore
saturo: il volume specifico della miscela può essere considerato come la media pesata dei
volumi specifici delle singole fasi in equilibrio. Si definisce una nuova proprietà, il titolo x,
che esprime la composizione massica della miscela:
Vl + Vvs
m l v l + mvs v vs
v=
=
m l + mvs
m l + mvs
mvs
x=
m l + mvs
Proiezione della superficie caratteristica sul diagramma p-v:
Il titolo è una grandezza adimensionale che può assumere valori compresi tra 0 ed 1:
mvs
x=
m l + mvs
v = (1 − x )v l + xv vs = v l + x (v vs − v l ) ⇒
(
v
x=
− vl
)
(vvs − v l )
Per un vapore saturo esiste una corrispondenza biunivoca tra v ed x: lo stato può
essere caratterizzato dalla coppia (p,x) o (T,x).
Per x=0 v=vl cioè siamo sulla curva limite inferiore.
Per x=1 v=vvs cioè siamo sulla curva limite superiore.
Per 0<x<1 siamo sotto la curva a campana.
Il luogo dei punti con egual titolo definisce le curve isotitoloconvergenti tutte nel punto
critico.
Proiezione della superficie caratteristica sul diagramma T-s per una sostanza
pura con una sola fase solida che fondendo espande
S l + S vs
ml
mvs
s=
=
sl +
svs =
m l + mvs m l + mvs
m l + mvs
= (1 − x )sl + xsvs
a-b isoterma del punto triplo: essa delimita la zona
bifasica liquido-aeriforme con le curve limiti;
Dalla conoscenza di s e T(e quindi della p corrispondente) è possibile determinare i valori
dell’entropia specifica del liquido saturo e del vapore saturo secco, dunque del titolo della
miscela.
L’area sottesa ad una trasformazione internamente reversibile sul piano Ts
rappresenta la quantità di energia specifica scambiata nel modo calore: l’area sottesa
al tratto di isobara-isoterma tra le curve limiti rappresenta l’entalpia di fusione.
Poiché le proprietà della sostanza in fase liquida sono poco sensibili alla variazione di
pressione, le isobare si addensano sulla curva limite inferiore: in due stati di equilibrio
caratterizzati dalla stessa T e da p differenti i valori delle entropie specifiche di fatto
coincidono.
La regione del liquido è praticamente coincidente con la curva limite inferiore.
T
⎛ ∂T ⎞
=
⎜
⎟
⎝ ∂s ⎠ p c p
Valutazione della pendenza di un’isobara: curva monotonicamente crescente con
concavità rivolta verso l’asse positivo della temperatura.
Se ci spostiamo lungo un’isobara (f-h) verso valori crescenti di T si nota un aumento
della pendenza della curva in quanto è trascurabile la variazione di cp rispetto alla
variazione di T.
La sottotangente (g-h)rappresenta il cp in quel punto.
L’isobara critica ha un flesso orizzontale in corrispondenza del punto critico che
coincide con il massimo della curva a-c-b.
Per un generico stato l’isocora e l’isobara ad esso relative (f) sono tali che la
pendenza della prima è sempre maggiore della pendenza della seconda:
T
⎛ ∂T ⎞
⎟ =
⎜
⎝ ∂s ⎠ v c v
c p > cv
La sottotangente intercettata dalla tangente nel punto considerato rappresenta il cv
in quel punto.
Nel piano Ts le derivate delle isobare e delle isocoe presentano una discontinuità in
corrispondenza della curva limite superiore.
valida per tutte le sostanze pure
⎛ ∂ T ⎞ ⎛ ∂T ⎞
⎜
⎟ >⎜
⎟
⎝ ∂s ⎠ v ⎝ ∂s ⎠ p
Dalle relazioni di Gibbs segue che le aree sottese da isocore e isobare rappresentano
rispettivamente le variazioni di energia interna e di entalpia specifica.
Si riporta il diagramma Ts per l’aria: lo stato di riferimento scelto è T=0°C, p=1atm; per
tale stato si ritiene arbitrariamente h=s=0.
Proiezione della superficie caratteristica sul diagramma h-s (Mollier)
Usato per il calcolo delle proprietà nei cicli diretti
dh = cp(T)dT
Nella regione bifasica le isobare-isoterme hannno un
andamento lineare:
Dalla II equazione di Gibbs si deduce che
spostandosi lungo un’isoentalpica verso s crescenti,
la p decresce.
⎛ ∂h ⎞
⎜ ⎟ =T
⎝ ∂s ⎠ p
⎛ ∂h ⎞
= Tc
⎜ ⎟
⎝ ∂s ⎠ p = pc
L’isobara d-e ha pendenza maggiore
della a-b; si noti che la temperatura
di saturazione corrispondente alla
pressione relativa alla curva d-e è
maggiore di quella corrispondente
alla curva a-b. Si deduce che il punto
critico non è il massimo della curva
a-c-b.
In corrispondenza della curva limite superiore al diminuire di p le
isoterme tendono a diventare orizzontali: per i gas ideali è h=h(T)
Le curve a titolo costante individuano
sulle isoterme segmenti proporzionali ad
(x-1) ed x.
Percorrendo le isobare nel verso delle T crescenti la pendenza va
aumentando:le isobare presentano la concavità rivolta verso l’asse
positivo dell’entalpia.
Si riporta il diagramma di Mollier per l’acqua: lo stato di riferimento è quello in cui si
ha solo liquido saturo al punto triplo; si ritiene arbitrariamente h=s=0.
Proiezione della superficie caratteristica sul diagramma p-s per una sostanza pura
Usato per il calcolo delle proprietà nei cicli inversi
Le isoterme hanno un andamento praticamente orizzontale nella zona dei liquidi: la
dipendenza dell’entalpia di un liquido dalla pressione è praticamente trascurabile. Nella
zona del vapore surriscaldato assume invece una pendenza negativa e tende a diventare
verticale nel campo delle basse pressioni: l’entalpia di un aeriforme a bassa p è funzione
solo di T.
La lunghezza del tratto di isobara nelle miscele bifasiche rappresenta
l’entalpia di fusione a quella pressione di saturazione: al crescere di p
la lunghezza dei segmenti diminuisce.
1
⎛ ∂p ⎞
=
⎜
⎟
Le isoentropiche hanno in ciascun punto pendenza pari alla densità nel punto stesso: dalla II eq. Di Gibbs
⎝ ∂h ⎠ s v
Le isoentropiche hanno un andamento praticamente lineare nella zona dei liquidi e assumono una pendenza via via
decrescente nel passaggio dalla zona bifasica a quella del vapore surriscaldato.
Si riporta il diagramma ph per il Freon-12: lo stato di riferimento è quello individuato
da T= - 40°C e p = 0.0641MPa; si ritiene arbitrariamente h=s=0.