Document

Teorema di Talete
Un fascio di rette parallele determina su due
trasversali classi di segmenti proporzionali.
A
A’
B
B’
C
C’
AB:BC=A’B’:B’C’
Applicazione Teorema Talete:
Trovare il quarto proporzionale
a,b,c chi è x tale che a:b=c:x?
Teorema (Bisettrice interna di un angolo)
La bisettrice interna di un triangolo divide il
lato opposto in parti proporzionali agli altri
due lati.
C
A
Hp:
CD bisettrice
D
B
Th:
AD : DB = AC : BC
Teorema
Se una semiretta uscente da un vertice di un
triangolo divide il lato opposto in parti
proporzionali agli due lati, essa è la
bisettrice.
Teorema
Dati in un certo ordine quattro segmenti se
essi sono in proporzione, il prodotto dei
medi è uguale al prodotto degli estremi.
AB:CD=EF:GH
AB*GH=CD*EF
In particolare se AB:CD=CD:EF  CD²=AB*EF
COEFFICIENTE DI PROPORZIONALITÀ:
Consideriamo due classi di grandezze
proporzionali:
-a, b, c,…
- a’, b’, c’,…
a  a’
b  b’
c  c’
a:b=a’:b’
Consideriamo le proporzioni
a : b = a’ : b’
a : a’ = b : b’
a/a’ = b/b’ = k coefficiente di proporzionalità
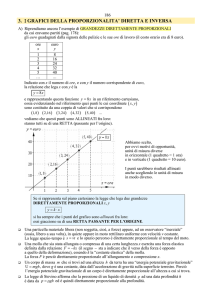
Se y è un elemento della prima classe e x è
l’elemento corrispondente nell’altra classe si
può scrivere y/x = k oppure y=kx
Si dice che y è direttamente proporzionale a x
Due classi di grandezze in corrispondenza
biunivoca si dicono PROPORZIONALI (o
DIRETTAMENTE proporzionali) quando è
costante il rapporto tra i loro elementi
corrispondenti.
y/x = k (ovvero y=kx)
Ad esempio: insieme dei rettangoli con la
stessa altezza  la classe delle aree e delle
basi sono direttamente proporzionali
Due classi di grandezze in corrispondenza
biunivoca si dicono INVERSAMENTE
PROPORZIONALI quando il prodotto tra i
loro elementi corrispondenti è costante:
xy = k
Esempio: insieme dei rettangoli con la
stessa area la classe delle basi e la classe
delle altezze sono inversamente
proporzionali.