Scheda n.1
Lavoro individuale di matematica
classi 4C e 4D
QUALCHE INDICAZIONE PER IL LAVORO INDIVIDUALE
•
•
•
•
•
Svolgi tutti gli esercizi proposti che sei capace di fare su fogli protocollo che dovrai consegnare
entro lunedì 21 febbraio.
Il ripasso della teoria non dovrebbe richiederti molto tempo (circa 30 minuti), non farlo però in modo
superficiale: non è irrilevante sapere se la traslazione è a destra piuttosto che a sinistra o se si ha una
dilatazione piuttosto che una contrazione
Gli esercizi dell’applicazione 1 sono molto veloci (circa 30 minuti), non richiedono conti, ma solo la
conoscenza delle notazioni utilizzate e della teoria ripassata.
Nell’applicazione 2 traccia i grafici nel modo più accurato possibile, fissando la consueta scala (cioè 12
quadretti per π o se ti è più comodo per 2π) ed evidenziando grafici ed assi finali. Per la determinazione delle
intersezioni con gli assi, quel che puoi deducilo dal grafico, altrimenti per le intersezioni con l’asse x risolvi
l’equazione f(x)=0 e per quella con l’asse y calcola f(0). Controlla i grafici con il programma winplot. Per le
prime 7 funzioni non sono necessari passaggi preliminari, quindi dovresti riuscire a fare il grafico e trovare le
intersezioni in circa 10- 15 minuti ciascuna, per le altre invece è necessario qualche passaggio prima di
tracciare il grafico quindi potresti impiegare un po’ di tempo in più.
Svolgi il test riportato nell’applicazione 3 una volta prima di ripassare, poi dopo aver ripassato e svolto
qualche esercizio, potrai così notare il tuo miglioramento… speriamo!
Il tempo per svolgere questa scheda dovrebbe essere complessivamente di circa 5 ore, organizza il tuo lavoro
settimanale.
TEORIA
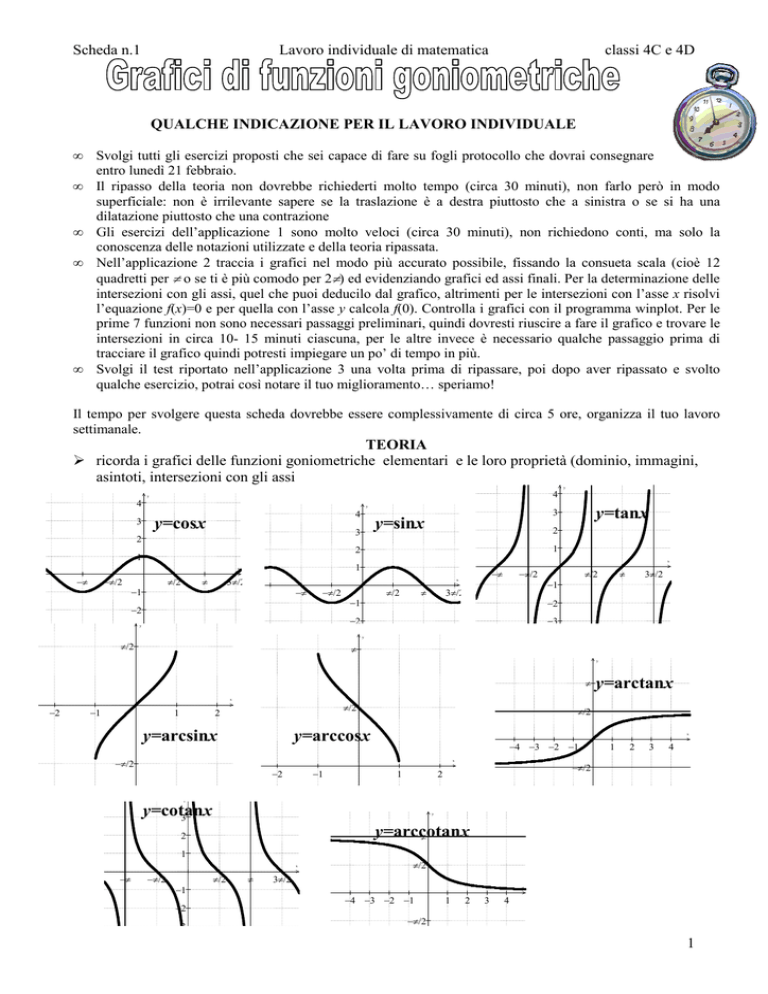
ricorda i grafici delle funzioni goniometriche elementari e le loro proprietà (dominio, immagini,
asintoti, intersezioni con gli assi
4
3
4
y
y=cosx
1
π/2
−1
π
x
1
x
3π/2
−π
x
−π
−π/2
−2
π/2
−1
π
−π/2
3π/2
y
π/2
−1
π
3π/2
−2
−2
−3
y=tanx
2
2
1
−π/2
3
y=sinx
3
2
−π
y
4
y
−3
y
π/2
π
y
π
x
−2
−1
1
π/2
2
y=arcsinx
π/2
y=arccosx
−π/2
x
−4 −3 −2 −1
x
−2
−1
y=arctanx
1
1
2
3
4
−π/2
2
4
y=cotanx
3
y
y=arccotanx
π
2
1
x
−π
−π/2
−1
−2
−3
π/2
π
π/2
3π/2
x
−4 −3 −2 −1
1
2
3
4
−π/2
1
Scheda n.1
Lavoro individuale di matematica
classi 4C e 4D
Ricorda le trasformazioni :
b>0
b<0
Traslazione
verticale
b<0
y = f ( x) + b
- se b > 0 si sposta il grafico verso l’alto, oppure
l’asse orizzontale verso il basso
- se b < 0 si sposta il grafico verso il basso, oppure
l’asse orizzontale verso l’alto
b>0
a>0
Traslazione
orizzontale
y=
y = f ( x + a)
- se a > 0 si sposta il grafico verso sinistra, oppure
l’asse verticale verso destra
- se a < 0 si sposta il grafico verso destra, oppure
l’asse verticale verso sinistra
a<0
a<0
a>0
Simmetria
rispetto
all’asse x
y = − f (x)
Simmetria
rispetto
all’asse y
y = f (− x)
Dilatazione
o
contrazione
verticale
y = kf (x) (gli zeri della funzione non cambiano)
- se k>1 si ha una dilatazione
- se 0<k<1 si ha una contrazione
Dilatazione
o
contrazione
orizzontale
y = f (kx) (non cambia l’intercetta della funzione)
- se k>1 si ha una contrazione
- se 0<k<1 si ha una dilatazione
Modulo su
tutto
y = f (x)
si ribaltano rispetto all’asse x le parti negative
Modulo su
tutte le x
y = f (x)
si considerano i punti del grafico con le x positive,
più i corrispondenti simmetrici rispetto all’asse delle
ordinate.
2
Scheda n.1
Lavoro individuale di matematica
classi 4C e 4D
Ricorda che le funzioni lineari si rappresentano, dopo averle riscritte utilizzando il metodo
dell’angolo aggiunto, cioè:
y = a cos x + b sin x = a 2 + b 2 cos( x − α )
a
b
con α tale che cos α =
e sin α =
a 2 + b2
a2 + b2
Più in generale, il metodo dell’angolo aggiunto si può applicare quando compaiono seno e coseno di 1°
grado con lo stesso argomento
Ricorda che le funzioni di 2° grado si rappresentano dopo aver abbassato di grado utilizzando le
formule di duplicazione del coseno e del seno, quindi
1 − cos 2 x
1
1 + cos 2 x
sin 2 x =
sin x cos x = sin 2 x
cos 2 x =
2
2
2
Più in generale
1 + cos[2 g ( x)]
1 − cos[2 g ( x)]
1
cos 2 [g ( x)] =
sin 2 [g ( x)] =
sin[g ( x)]cos[g ( x)] = sin[2 g ( x)]
2
2
2
APPLICAZIONE 1
Data la funzione f(x) scrivi l’espressione analitica di g(x) e h(x) e specifica come si ottiene il grafico di
g(x) a partire da quello di f(x) (senza però tracciarlo)
f(x)
g(x)
h(x)
y
=
tan
x
g
(
x
)
=
f
(
2
x
)
g
(
x
)
=
2
f ( x)
1
2
y = cot anx
g ( x) = f (2 + x)
g ( x) = 2 + f ( x)
3
y = arccos x
g ( x) = − f ( x)
g ( x) = f (− x)
4
y = sin x
g ( x) = f ( x)
g ( x) = f ( x )
5
y = arcsin x
6
y = cos x
g ( x) = f (2 x − 1)
g ( x) = f (2( x − 1))
7
y = arctan x
g ( x) = f ( x) − 1
g ( x) = f ( x − 1)
g ( x) = f ( x − 1 )
g ( x) = f ( x) − 1
APPLICAZIONE 2
Traccia i grafici delle seguenti funzioni per ciascuna indica:
- se è periodica, il periodo
- le intersezioni con gli assi cartesiani.
funzione
π
1
y = 3tg ( x +
2
y = cos x − 2
3
4
6
5
)
sin( 2 x)
y=
−1
3
π
y = sin( x − )
6
7
8
9
10
π
)
6
π
y = cos(2 x − )
3
2
2 − cos x
y=
3
y = sin( x −
y = 1 − sin x cos x
y = 3 cos x − 4 sin x
11
y = cos x + sin x − 1
12
y=
13
sin 2 x
1 − cos x
1
y=
tan 3 x
14
y = cos 2 x + sin x cos x
15
y = sin 2 x + 3 sin x cos
APPLICAZIONE 3
Svolgi il test che trovi sul sito
3