MATEMATICA
a.a. 2014/15
3. CALCOLO DIFFERENZIALE (I parte):
Definizione, proprietà e calcolo delle
derivate. Derivate di funzioni algebriche e
trascendenti. Massimi, minimi, flessi e
studio qualitativo di funzioni.
Definizione
Consideriamo una funzione continua f.
Accanto ai valori della funzione stessa, interessa spesso considerare
la rapidità con cui tali valori variano al variare della variabile
indipendente.
Ad esempio se x indica il tempo e y la posizione nella quale viene a
trovarsi all’istante x un punto che si muove su una guida (che
ipotizziamo sia rettilinea). La maggiore o minore rapidità con cui la
posizione del punto varia nel tempo dà luogo a una nuova grandezza:
la velocità nel punto.
La nozione di derivata consente di dare un significato rigoroso a
queste considerazioni intuitive: la velocità infatti viene a essere la
derivata della funzione che esprime la legge oraria del moto e
l’accelerazione è definita come la derivata della velocità
Definizione
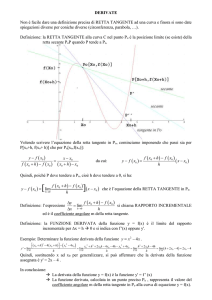
Fissiamo un punto x0 appartenente all’insieme di definizione della funzione
y=f(x) e sia P0 = (x0, f(x0)) il punto di ascissa x0 appartenente al grafico della
funzione.
Consideriamo un ulteriore punto x1 anch’esso appartenente all’insieme di
definizione della funzione e sia P1 = (x1, f(x1)) appartenente al grafico della
funzione.
I due punti P0 e P1 individuano una retta secante al grafico.
Fermo restando il punto x0, immaginiamo di ripetere la costruzione, in modo
tale da scegliere x1 via via più vicino a x0. Al tendere di x1 a x0, il punto P1 si
avvicina al punto P0 e la retta secante tende ad assumere una posizione
limite t, che prende il nome di retta tangente al grafico nel punto P0.
∆( y)
∆ ( x)
Se P1 tende a P0
Definizione
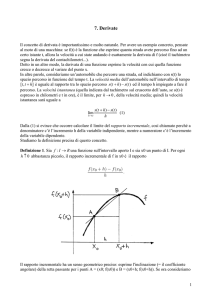
Dati una funzione y=f(x), definita in un intervallo [a,b] e due numeri reali e x0=x x1=x+h
interni all’intervallo, si chiama rapporto incrementale di f (relativo a h) la quantità:
∆y f ( x1 ) − f ( x0 ) f ( x + h ) − f ( x )
=
=
∆x
x1 − x0
h
dove spesso si indica
∆ ( x ) = x1 − x0
(incremento della variabile x) e analogamente
∆ ( y ) = f ( x1 ) − f ( x0 ) per indicare l’incremento della variabile y corrispondente
all’incremento ∆x della variabile X.
Il rapporto incrementale di f relativo a h è il coefficiente angolare della retta passante per
P0 e P1
Sulla base di tale notazione il coefficiente angolare della retta secante, che rappresenta
la variazione media, assume la forma di «rapporto incrementale»: ∆y
∆x
da cui l’equazione della retta secante sarà:
y=
f ( x1 ) − f ( x0 )
x1 − x0
( x − x0 ) + f ( x0 ) =
∆y
( x − x0 ) + f ( x0 )
∆x
Definizione
Passando al limite quando x1 tende a x0 , quindi attribuendo a h valori via via più
piccoli, il punto P1 si avvicina sempre di più al punto P0. Quando h tende a zero, il
coefficiente angolare della retta secante P1P0, ossia il rapporto incrementale, tende
al coefficiente angolare della tangente, che viene chiamato derivata della funzione
nel punto x0:
lim
x1→ x 0
f ( x1 ) − f ( x0 )
x1 − x0
∆y
= lim
= f ′ ( x0 )
∆x →0 ∆x
Se questo limite esiste finito, la retta tangente avrà quindi equazione:
y − f ( x0 ) = f ′ ( x0 )( x − x0 )
y = f ′ ( x0 )( x − x0 ) + f ( x0 )
Se esiste finito il limite specificato sopra, la funzione f è derivabile in x0. Il valore
del limite verrà detto derivata di f in x0 e indicato con il simbolo f’(x0) o con
df
( x ) e che possiamo riscrivere come:
dx
0
f ( x0 + h ) − f ( x0 )
df
f ′ ( x0 ) = ( x0 ) = lim
h →0
dx
h
dove: h=x1-x0 e x1=x0+h
Definizione
Il valore f’(x0) è per definizione la derivata prima di f in x0.
Non è detto che il limite esista finito! In altre parole non è sempre detto che si possa calcolare la
variazione istantanea.
Una funzione derivabile in x0 è necessariamente continua in x0
Una funzione y=f(x) si dice derivabile se ammette derivata in ogni punto del
suo insieme di definizione D.
Associando a ogni punto x dell’insieme di definizione di f(x) la corrispondente
derivata (calcolata nel punto x) si ottiene una nuova funzione, detta appunto
funzione derivata della funzione data. In simboli si avrà:
f ′ ( x) ,
df
dy
′
x
,
y
x
,
( ) ( ) ( x)
dx
dx
Si dimostra che le funzioni base già introdotte (polinomi, esponenziali e logaritmi,
funzioni trigonometriche) sono tutte derivabili.
Definizione
Una funzione si dice derivabile in un punto x se esiste la derivata f’(x). Affinché una
funzione sia derivabile in x occorre quindi che siano verificate le seguenti condizioni:
1. La funzione è definita in un intorno del punto x
2. Esiste il limite del rapporto incrementale, relativo a x, per h che tende a 0, cioè esiste
il limite destro e il limite sinistro di tale rapporto e tali limiti coincidono
3. Questo limite è un numero finito.
Qual è il rapporto tra continuità e derivabilità?
TEOREMA
Se f è derivabile in x0 allora f è continua in x0
DIMOSTRAZIONE
Per ipotesi,
lim
x → x0
f ( x ) − f ( x0 )
x − x0
esiste finito.
f ( x ) − f ( x0 )
f ( x ) − f ( x0 )
lim f ( x ) − f ( x0 ) = lim
⋅ ( x − x0 ) = lim
⋅ lim ( x − x0 ) = f ′ ( x0 ) ⋅ 0 = 0
x → x0
x → x0
x
→
x
x → x0
0
x − x0
x − x0
Quindi:
lim f ( x ) = f ( x0 )
x → x0
Calcolo di derivate: funzioni algebriche
Sia f: R → R la funzione costante f(x)=c per ogni x appartenente ad R. In questo caso
il rapporto incrementale, per h≠0 è:
f ( x + h) − f ( x)
h
=
c−c 0
= =0
h
h
Quindi il rapporto incrementale di una funzione costante è sempre nullo, per cui il limite
del rapporto incrementale è chiaramente sempre 0. Si è dimostrato quindi che:
f ( x) ≡ c ⇒ f ′ ( x) ≡ 0
La derivata di una funzione costante è identicamente nulla.
f ( x) = 3
f ′ ( x) = 0