Prova di recupero del debito formativo di matematica
02/11/09
A
Barrare la risposta esatta. Per ogni quesito, la risposta esatta è unica.
Ogni risposta esatta vale un punto, ogni risposta errata comporta una penalizzazione di 14 di punto.
La prova è superata ottenendo un punteggio complessivo almeno pari a 7,5
punti.
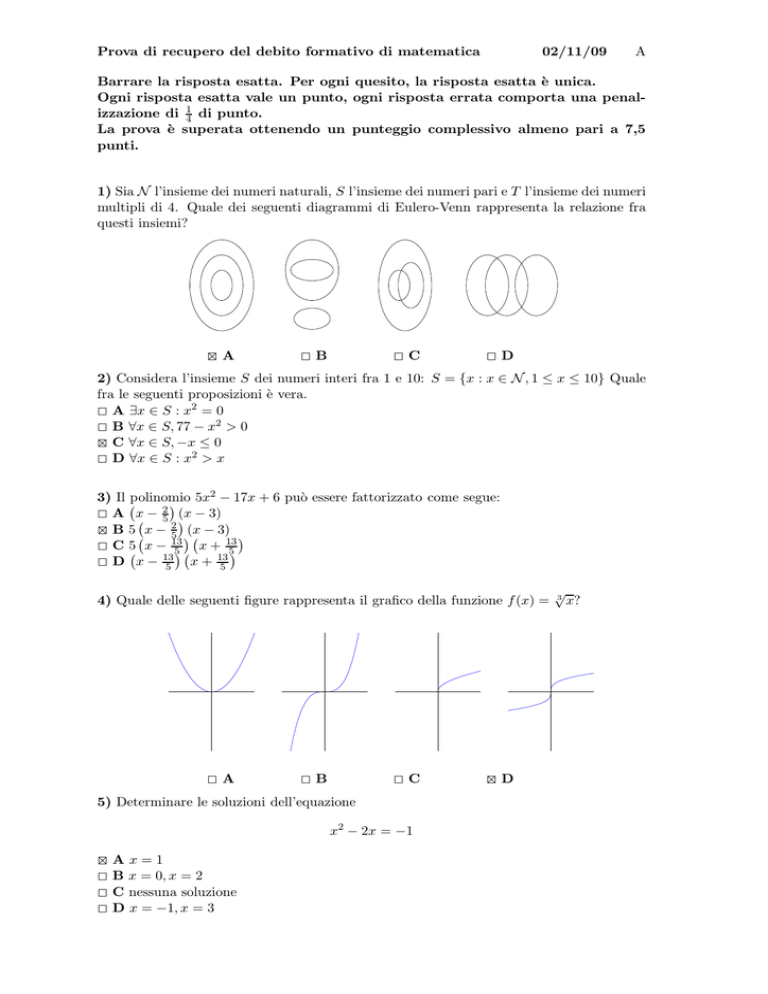
1) Sia N l’insieme dei numeri naturali, S l’insieme dei numeri pari e T l’insieme dei numeri
multipli di 4. Quale dei seguenti diagrammi di Eulero-Venn rappresenta la relazione fra
questi insiemi?
4A
2B
2C
2D
2) Considera l’insieme S dei numeri interi fra 1 e 10: S = {x : x ∈ N , 1 ≤ x ≤ 10} Quale
fra le seguenti proposizioni è vera.
2 A ∃x ∈ S : x2 = 0
2 B ∀x ∈ S, 77 − x2 > 0
4 C ∀x ∈ S, −x ≤ 0
2 D ∀x ∈ S : x2 > x
2
3) Il polinomio
5x − 17x + 6 può essere fattorizzato come segue:
2
2 A x − 5 (x − 3)
4 B 5 x − 25 (x − 3) x + 13
2 C 5 x − 13
5
5
13
2 D x − 5 x + 13
5
4) Quale delle seguenti figure rappresenta il grafico della funzione f (x) =
2A
2B
2C
5) Determinare le soluzioni dell’equazione
x2 − 2x = −1
4
2
2
2
Ax=1
B x = 0, x = 2
C nessuna soluzione
D x = −1, x = 3
4D
√
3
x?
6) Determinare le soluzioni della disequazione
x4 − 2x2 ≥ x3
2
2
2
4
A x ∈ − 12 , 0 ∪ [1, +∞)
B x ∈ (−∞, 0)
C x ∈ (−1, 1) ∪ [2, +∞)
D x ∈ (−∞, −1] ∪ {0} ∪ [2 + ∞)
7) Considera i punti P (1, −2) e Q(0, 1) nel piano cartesiano xOy. Determinare la lunghezza del segmento P¯Q.
√
√
2C2
2D 2
2 A 10
4 B 10
8) A cose è uguale log2 8?
4A3
2 B −2
2 D −3
2C0
9) Determinare l’equazione della retta passante per i punti P (1, 0) e Q(−2, 1).
2 A y = −3x + 1
2 B y = 3x + 1
4 C y = − 13 x + 31
2 D y = 31 x + 31
10) Fra i seguenti sistemi, quale è impossibile?
x+2>3
x−1>3
A :
B
:
(x + 2)2 > 1
(x + 2)2 > −1
4C :
11) Determinare il dominio T della funzione f (x) =
4 A T = [0, 1) ∪ (1, +∞)
2 B T = (1, +∞)
2 C T = (0, 1) ∪ (1, +∞)
2 D T = (−∞, 1) ∪ (1, +∞)
x+3>1
(x + 2)2 < −1
D :
x+2<3
(x + 2)2 < 1
√
x
x−1 .
12) Determinare il grafico della funzione f (x) = |x| − 2.
2A
4B
2C
2D
13) La soluzione della disequazione log(1 − x) > log x è:
2 A x < 21
4 B 0 < x < 12
2C0<x<1
2 D 12 < x < 1
14) La soluzione della disequazione ex+1 ≥ 2 è:
4 A x ≥ log 2 − 1
2 B x ≤ log 2 − 1
2 C x≥e−1
2 D la disequazione non ammette soluzioni reali
15) Il numero sen π2 è uguale a:
2 A −1
2B0
2C
1
2
4D1
Prova di recupero del debito formativo di matematica
02/11/09
B
Barrare la risposta esatta. Per ogni quesito, la risposta esatta è unica.
Ogni risposta esatta vale un punto, ogni risposta errata comporta una penalizzazione di 14 di punto.
La prova è superata ottenendo un punteggio complessivo almeno pari a 7,5
punti.
1) Sia N l’insieme dei numeri naturali, S l’insieme dei numeri multipli di 4 e T l’insieme
dei numeri multipli di 6. Quale dei seguenti diagrammi di Eulero-Venn rappresenta la
relazione fra questi insiemi?
2A
2B
4C
2D
2) Considera l’insieme S dei numeri interi fra 1 e 10: S = {x : x ∈ N , 1 ≤ x ≤ 10} Quale
fra le seguenti proposizioni è vera.
2 A ∃x ∈ S : x2 = 0
4 B ∀x ∈ S, x − 2 < x2
2 C ∀x ∈ S, 77 − x2 > 0
2 D ∀x ∈ S : x2 > x
2
3) Il polinomio
3x + 5x − 2 può essere fattorizzato come segue:
1
4 A 3 x − 3 (x + 2)
2 B x − 31 (x + 2)
2 C (x − 3) (x + 2)
2 D 3 (x − 1) (x + 2)
4) Quale delle seguenti figure rappresenta il grafico della funzione f (x) = x3 ?
2A
4B
2C
5) Determinare le soluzioni dell’equazione
x2 − 2x = −2
2
2
4
2
Ax=1
B x = 0, x = 2
C nessuna soluzione
D x = −1, x = 3
2D
6) Determinare le soluzioni della disequazione
2
2
4
2
A x ∈ − 12 , 0 ∪ [1, +∞)
B x ∈ (−∞, 0)
C x ∈ (−1, 1) ∪ [2, +∞)
D x ∈ (−∞, −1] ∪ {0} ∪ [2 + ∞)
x−2
≥0
x2 − 1
7) Considera i punti P (−1, −2) e Q(0, 1) nel piano cartesiano xOy. Determinare la
lunghezza del segmento P¯Q. √
√
2C2
2D 2
2 A 10
4 B 10
8) A cose è uguale log2 1?
2A3
2 B −2
4C0
9) Determinare l’equazione della retta passante per i punti P (−1, 0) e Q(2, 1).
2 A y = −3x + 1
2 B y = 3x + 1
2 C y = − 13 x + 31
4 D y = 31 x + 31
10) Fra i seguenti sistemi, quale è impossibile?
x+2>3
x+1>3
B :
4A :
2
(x + 2)2 > −2
(x + 2) < −2
C :
11) Determinare il dominio T della funzione f (x) =
2 A T = [0, 1) ∪ (1, +∞)
4 B T = (1, +∞)
2 C T = (0, 1) ∪ (1, +∞)
2 D T = (−∞, 1) ∪ (1, +∞)
q
x+1>0
(x + 2)2 > 0
2 D −3
D :
x+1<3
(x + 2)2 < 1
1
x−1 .
12) Determinare il grafico della funzione f (x) = − |x| − 2.
2A
2B
2C
4D
13) La soluzione della disequazione log x > log(1 − x) è:
2 A x < 21
2 B 0 < x < 12
2C0<x<1
4 D 12 < x < 1
14) La soluzione della disequazione ex+1 ≤ −2 è:
2 A x ≥ log 2 − 1
2 B x ≤ log 2 − 1
2 C x≥e−1
4 D la disequazione non ammette soluzioni reali
15) Il numero cos π2 è uguale a:
2 A −1
4B0
2C
1
2
2D1
Prova di recupero del debito formativo di matematica
02/11/09
C
Barrare la risposta esatta. Per ogni quesito, la risposta esatta è unica.
Ogni risposta esatta vale un punto, ogni risposta errata comporta una penalizzazione di 41 di punto.
La prova è superata ottenendo un punteggio complessivo almeno pari a 7,5
punti.
1) Sia S l’insieme dei numeri numeri multipli di 4, T l’insieme dei numeri numeri multipli
di 3 ed U l’insieme dei numeri dispari. Quale dei seguenti diagrammi di Eulero-Venn
rappresenta la relazione fra questi insiemi?
2A
2B
2C
4D
2) Considera l’insieme S dei numeri interi fra 1 e 10: S = {x : x ∈ N , 1 ≤ x ≤ 10} Quale
fra le seguenti proposizioni è falsa.
4 A ∀x ∈ S, 77 − x2 > 0
2 B ∀x ∈ S, x − 2 < x2
2 C ∄x ∈ S : x2 = 15
2 D ∀x ∈ S, −x ≤ 0
3) Il polinomio 2x2 − 7x + 3 può essere fattorizzato come segue:
2 A 2 (x − 1) (x − 3)
2 B x − 12 (x
− 3)
4 C 2 x − 12 (x − 3)
2 D 2 x − 32 x − 21
4) Quale delle seguenti figure rappresenta il grafico della funzione f (x) =
2A
2B
4C
5) Determinare le soluzioni dell’equazione
x2 − 2x = 3
2
2
2
4
Ax=1
B x = 0, x = 2
C nessuna soluzione
D x = −1, x = 3
2D
√
x?
6) Determinare le soluzioni della disequazione
2x3 + x < x2
2
4
2
2
A x ∈ − 12 , 0 ∪ [1, +∞)
B x ∈ (−∞, 0)
C x ∈ (−1, 1) ∪ [2, +∞)
D x ∈ (−∞, −1] ∪ {0} ∪ [2 + ∞)
7) Considera i punti P (1, 2) e Q(0, −1) nel piano cartesiano xOy. Determinare la lunghezza del segmento P¯Q.
√
√
2C2
2D 2
2 A 10
4 B 10
8) A cose è uguale log2 14 ?
2A3
4 B −2
2 D −3
2C0
9) Determinare l’equazione della retta passante per i punti P (1, −2) e Q(0, 1).
4 A y = −3x + 1
2 B y = 3x + 1
2 C y = − 31 x + 31
2 D y = 31 x + 31
10) Fra i seguenti sistemi, quale è impossibile?
x+2>0
x−1>3
A :
B
:
(x − 3)2 > 1
(x − 3)2 > −1
C :
11) Determinare il dominio T della funzione f (x) =
2 A T = [0, 1) ∪ (1, +∞)
2 B T = (1, +∞)
4 C T = (0, 1) ∪ (1, +∞)
2 D T = (−∞, 1) ∪ (1, +∞)
x+3 > 1
(x − 3)2 < 1
4D :
x+2<3
(x − 3)2 < −2
1
log x .
12) Determinare il grafico della funzione f (x) = |x − 2|.
4A
2B
2C
2D
13) La soluzione della disequazione log(2x) > log(1 − x) è:
4 A 13 < x < 1
2B0<x<1
2 C 0 < x < 31
2 D x < 31
14) La soluzione della disequazione ex+1 ≤ 2 è:
2 A x ≥ log 2 − 1
4 B x ≤ log 2 − 1
2 C x≥e−1
2 D la disequazione non ammette soluzioni reali
15) Il numero cosπ è uguale a:
4 A −1
2B0
2C
1
2
2D1
Prova di recupero del debito formativo di matematica
02/11/09
D
Barrare la risposta esatta. Per ogni quesito, la risposta esatta è unica.
Ogni risposta esatta vale un punto, ogni risposta errata comporta una penalizzazione di 14 di punto.
La prova è superata ottenendo un punteggio complessivo almeno pari a 7,5
punti.
1) Sia S l’insieme dei numeri numeri multipli di 4, T l’insieme dei numeri numeri multipli
di 2 ed U l’insieme dei numeri dispari. Quale dei seguenti diagrammi di Eulero-Venn
rappresenta la relazione fra questi insiemi?
2A
4B
2C
2D
2) Considera l’insieme S dei numeri interi fra 1 e 10: S = {x : x ∈ N , 1 ≤ x ≤ 10} Quale
fra le seguenti proposizioni è falsa.
2 A ∃x ∈ S : x2 > 77
2 B ∀x ∈ S, x − 2 < x2
2 C ∀x ∈ S, −x ≤ 0
4 D ∃x ∈ S : x2 = 15
3) Il polinomio 5x2 − 7x − 6 può essere fattorizzato come segue:
2 A 5 (x − 3) (x + 2)
2 B x + 35 (x
− 2)
2 C 5 x + 25 (x − 3)
4 D 5 x + 35 (x − 2)
4) Quale delle seguenti figure rappresenta il grafico della funzione f (x) = x4 ?
4A
2B
2C
5) Determinare le soluzioni dell’equazione
x2 − 2x = 0
2
4
2
2
Ax=1
B x = 0, x = 2
C nessuna soluzione
D x = −1, x = 3
2D
6) Determinare le soluzioni della disequazione
1
≤ 2x − 1
x
4
2
2
2
A x ∈ − 12 , 0 ∪ [1, +∞)
B x ∈ (−∞, 0)
C x ∈ (−1, 1) ∪ [2, +∞)
D x ∈ (−∞, −1] ∪ {0} ∪ [2 + ∞)
7) Considera i punti P (−1, −2) e Q(0, −1) nel piano cartesiano xOy. Determinare la
lunghezza del segmento P¯Q. √
√
2 A 10
2 B 10
2C2
4D 2
8) A cose è uguale log 1 8?
2
2A3
2 B −2
4 D −3
2C0
9) Determinare l’equazione della retta passante per i punti P (−1, −2) e Q(0, 1).
2 A y = −3x + 1
4 B y = 3x + 1
2 C y = − 13 x + 31
2 D y = 31 x + 31
10) Fra i seguenti sistemi, quale è impossibile?
x+2>3
x+1 > 2
A :
4B :
(x + 2)2 > 1
(x − 1)2 < −1
C :
11) Determinare il dominio T della funzione f (x) =
2 A T = [0, 1) ∪ (1, +∞)
2 B T = (1, +∞)
2 C T = (0, 1) ∪ (1, +∞)
4 D T = (−∞, 1) ∪ (1, +∞)
x + 3 > −1
(x − 1)2 < 1
D :
x−1<3
(x − 1)2 < 1
1
√
3
x−1
12) Determinare il grafico della funzione f (x) = − |x − 2|.
2A
2B
4C
2D
13) La soluzione della disequazione log(2x) < log(1 − x) è:
2 A 13 < x < 1
2B0<x<1
4 C 0 < x < 31
2 D x < 31
14) La soluzione della disequazione ex+1 ≥ −2, è:
2 A x ≥ log 2 − 1
2 B x ≤ log 2 − 1
2 C x≥e−1
4 D la disequazione è verificata ∀x reale
15) A cosa è uguale cos π3 :
2 A −1
2B0
4C
1
2
2D1










