Lezione mecc n.15
pag
Argomenti di questa lezione (esercitazione)
• Vari esercizi e parti di esercizi di ricapitolazione sulla
dinamica traslazionale (di una o più particelle)
1
Lezione mecc n.15
pag
2
20 luglio 2006
k
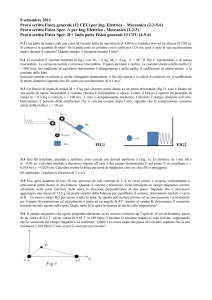
Esercizio 1
Un corpo A di massa
m scivola su una guida
liscia orizzontale, sulla
quale poggia un secondo corpo, B, di massa M. Una molla di costante
elastica k e massa trascurabile è attaccata al corpo B. Quando A, all’istante
t=0, urta la molla, vi rimane attaccato. Inizialmente B è fermo e A si
muove a velocità v0 verso di esso.
A, m
B, M
a) Indicare (giustificando le risposte) quali quantità meccaniche, fra quelle utili a
rispondere ai quesiti seguenti, restano costanti prima dell’urto e quali dopo
l’urto.
b) Calcolare la velocità del centro di massa del sistema prima e dopo l’urto.
c) Calcolare la massima compressione ∆xmax della molla.
d) Determinare a quali istanti la molla risulta massimamente compressa.
e) Scrivere la velocità del corpo A rispetto al tavolo ad un istante generico
successivo all’urto
6 settembre 2005 Esercizio 1
Il sistema rappresentato in figura è
M
costituito da due corpi parallelepipedi di
2M
massa M e 2M sovrapposti, poggiati su un
tavolo orizzontale. Fra i due corpi così
come fra il tavolo ed il corpo inferiore ha
m
luogo attrito radente descritto dai
coefficienti µD e µS. Il corpo inferiore è
connesso ad un terzo corpo di massa m sospeso fuori del tavolo, per mezzo
una corda inestensibile e di massa trascurabile, rinviata da una carrucola
anch’essa di massa trascurabile e libera di ruotare senza attriti.
Supponendo noti i valori di M, µD e µS, ed assumendo che il sistema sia
immobile al tempo t=0, stabilire per quali valori di m il sistema resta
immobile. Stabilire inoltre per quali valori di m, pur non verificandosi le
condizioni di staticità, non si osserva strisciamento fra i due corpi
appoggiati. In quest’ipotesi, determinare con quale velocità scende il corpo
m quando esso si è spostato di un tratto h, e determinare l’istante al quale
ciò si verifica.
[suggerimento: determinare tensione della corda e accelerazione dei corpi nell’ipotesi che ci sia
strisciamento solo fra parallelepipedo inferiore e tavolo]
Lezione mecc n.15
pag
21 luglio 2007 Esercizio 2
Un oggetto di massa M si muove lungo una coordinata x è
sottoposto ad una forza conservativa F cui è associata un
energia potenziale U, la quale dipende dalla posizione x
secondo la legge
U(x)=2Bx3−3Αx2,
con A costante positiva e B costante da determinare.
a) Al variare di B, stabilire se esistono punti di equilibrio,
qual è la loro ascissa (esprimere la posizione di tali punti
in termini di A e B), quali sono di equilibrio stabile e
quali di equilibrio instabile.
b) In una condizione (cioè per un valore di B) sotto cui
esiste un punto di equilibrio stabile ed uno di equilibrio
instabile, determinare con quale velocità deve muoversi
l’oggetto nel punto di equilibrio stabile per potersi
allontanare indefinitamente da tale punto.
c) Determinare la frequenza con cui l’oggetto compie
piccole oscillazioni intorno al punto di equilibrio stabile.
3
Lezione mecc n.15
pag
4
11 settembre 2003 Esercizio 2
Un blocco di massa M
scende senza incontrare
attriti lungo un piano di
lunghezza L inclinato di un
angolo θ rispetto all’orizzontale. Alla base del piano inclinato, il blocco
trova un piano orizzontale scabro (con coefficienti d’attrito µD e µS noti) su
cui procede per un altro tratto L prima di urtare in maniera perfettamente
anelastica un corpo di massa 2M. Dopo l’urto i due corpi procedono fino a
fermarsi.
a) Sapendo che il primo corpo inizia a scivolare (partendo da fermo) al
tempo t=0, determinare l’istante a cui avviene l’urto.
b) Calcolare quanta energia viene dissipata prima dell’urto.
c) Calcolare quanta energia viene dissipata nell’urto e quanta dopo
l’urto.
d) Determinare quanto spazio percorrono i due corpi dopo l’urto, prima
di fermarsi, e quanto tempo impiegano a percorrerlo.
1 ottobre 2001 Esercizio 1
Un’automobile (massa m) urta contro un
vagone ferroviario (massa M) ed i due
mezzi restano incastrati dopo la collisione,
la quale può essere considerata istantanea.
Il vagone è inizialmente fermo sul binario, mentre la macchina giunge a
velocità V, diretta a 30° rispetto al binario. Il vagone non deraglia, in altri
termini, dopo l’urto i due mezzi si muovono insieme lungo il binario.
Determinare:
a) l’energia cinetica della macchina prima dell’urto;
b) la velocità finale dei due mezzi;
c) l’energia dissipata nell’urto.
d) I valori numerici (MKS) delle quantità precedenti se m=1.1t, M=12t,
V=45km/h.
Lezione mecc n.15
pag
5
29 aprile 2005 Esercizio 2
Un oggetto di massa M si muove in direzione verticale sotto l’azione della
forza peso e di una forza d’attrito viscoso descritta dalla relazione F=−γv.
Sapendo che al tempo t=0 esso si muove verso l’alto con velocità v0,
a) determinare l’istante t1 al quale si ferma;
b) calcolare lo spazio percorso prima di arrestarsi;
c) scrivere un’equazione per determinare l’istante t2 al quale l’oggetto
torna a transitare nel punto che occupava a t=0; risolvere tale
equazione o chiarire il motivo per cui non si sa risolverla;
d) calcolare la quantità di energia che è stata dissipata per attrito durante
la salita e cioè nell’intervallo di tempo fra 0 e t1.
[Suggerimento: iniziare indicando chiaramente qual è l’equazione del
moto che si deve risolvere e quali sono condizioni iniziali con cui si
devono determinare le leggi orarie per velocità e posizione]
19 luglio 2004
Esercizio 1
Un veicolo di massa m si muove
F0
orizzontalmente senza incontrare
altri attriti oltre a quello con l’aria,
il quale è di tipo viscoso ed è
descritto dall’espressione F(v)=-γv, dove F è la forza, v la velocità e γ una
costante assegnata. Al veicolo, che inizialmente è fermo, viene applicata
per un tempo ∆t una forza costante F0 diretta orizzontalmente, che poi
viene rimossa.
a) Scrivere le equazioni del moto valide prima e dopo la rimozione
della forza;
b) Determinare le leggi orarie della velocità valide per 0<t<∆t e per
t>∆t;
c) Calcolare il lavoro svolto dalla forza applicata;
d) Determinare lo spostamento complessivo del corpo, dopo un tempo
indefinitamente lungo.