I_prova__Settembre_2005

Cognome e nome:
A.A. 2003/2004
Fisica I (Meccatronica)
I APPELLO SETTEMBRE (8/9/2005)
Luogo e data di nascita
Matricola
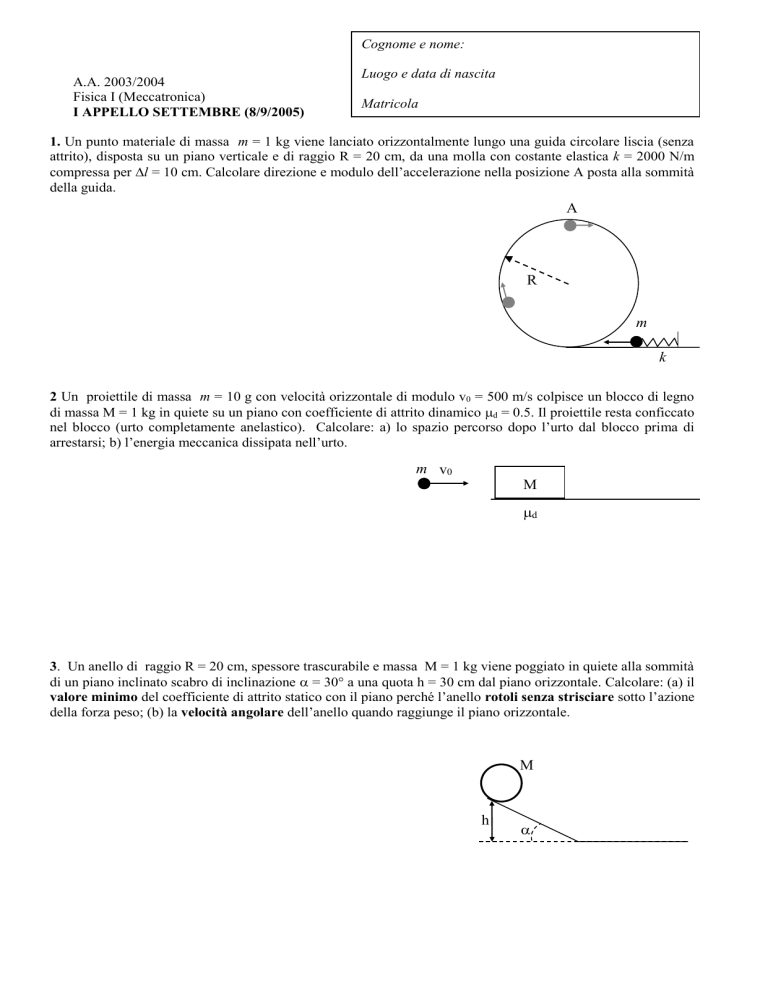
1. Un punto materiale di massa m = 1 kg viene lanciato orizzontalmente lungo una guida circolare liscia (senza
attrito), disposta su un piano verticale e di raggio R = 20 cm, da una molla con costante elastica k = 2000 N/m
compressa per l = 10 cm. Calcolare direzione e modulo dell’accelerazione nella posizione A posta alla sommità
della guida.
A
R
m
k
2 Un proiettile di massa m = 10 g con velocità orizzontale di modulo v0 = 500 m/s colpisce un blocco di legno
di massa M = 1 kg in quiete su un piano con coefficiente di attrito dinamico d = 0.5. Il proiettile resta conficcato
nel blocco (urto completamente anelastico). Calcolare: a) lo spazio percorso dopo l’urto dal blocco prima di
arrestarsi; b) l’energia meccanica dissipata nell’urto.
m v0
M
d
3. Un anello di raggio R = 20 cm, spessore trascurabile e massa M = 1 kg viene poggiato in quiete alla sommità
di un piano inclinato scabro di inclinazione  = 30° a una quota h = 30 cm dal piano orizzontale. Calcolare: (a) il
valore minimo del coefficiente di attrito statico con il piano perché l’anello rotoli senza strisciare sotto l’azione
della forza peso; (b) la velocità angolare dell’anello quando raggiunge il piano orizzontale.
M
h

QUESITI (oltre alle formule necessarie MAX 30 parole ognuno)
A) Scrivere l’espressione più generale di un moto armonico unidimensionale specificando il significato dei termini.
B) Cosa si intende per sistema di riferimento inerziale?
C) Scrivere l’espressione del Teorema di Konig per l’energia cinetica di sistema di punti materiali specificando il
significato dei termini.
.
D) Quale è la definizione e le caratteristiche di un asse principale di inerzia?
E) Scrivere l’espressione del Teorema di Huygens-Steiner per un corpo rigido specificando il significato dei termini
SOLUZIONI ESERCIZI
1)
per la conservazione dell'energia:
1
1
kl 2  mv 2A  2mgR
2
2

vA 
kl 2  4mgR  3.49 m/s
in A l’accelerazione ha la sola componente radiale:
a  an 
v 2A
R
 60.9 m/s 2
per la conservazione della quantità di moto nell’urto anelastico la velocità del blocco subito
dopo l’urto sarà:
2)
V
m
v0
Mm
per il teorema del lavoro (della forza di attrito) e dell'energia cinetica:
2
1
M  m V 2  1 m v 20  M  m gd s
2
2 M  m 

s 
1
m2
v 20
2
2 M  m  g d
 2.5 m
quindi:
T 
1
1 m2
1
mv 20 
v 20  mv 20
2
2 M  m
2

m 
1 
  1238 J  0.99T0
 M  m 
Per garantire il puro rotolamento, ovvero l’equilibrio statico del punto di contatto, la forza di
attrito dovrà eguagliare la componente tangenziale al piano della forza peso:
3)
FA  Mg sen   S R N   S Mg cos
da cui:
 S  tg  0.58
per la conservazione dell'energia meccanica:
1
1
1
1
2
mv 2 
mR 2 2  mωR  
m 2 R 2  mgh
2
2
2
2

gh
 8.57 rad/s
R
da cui :