A.A. 2013-14
Fisica Generale
24-06-14
ESERCIZIO 1
La cabina di una funicolare si muove con accelerazione costante a lungo
un pendio di angolo α=30°. Un punto materiale di massa m è disposto
sul pavimento, scabro, con coefficiente attrito statico tra punto e
pavimento µs=0.4. Calcolare quanto il
massimo
valore
dell’accelerazione della cabina affinché il punto materiale rimanga
fermo durante il moto.
Soluzione
Nel sistema di riferimento non inerziale della cabina, il corpo di massa m è sottoposto alla forza peso e
alla reazione normale, entrambe verticali, all’attrito diretto orizzontalmente lungo il piano della cabina
e a una forza fittizia diretta parallelamente al piano inclinato, verso il basso. Preso un sistema di
riferimento con un asse x orizzontale e un asse y verticale, la soluzione dell’equazione di Newton con
accelerazione nulla da:
−
−
=0
− =0
) da cui:
Imponendo la condizione
≤
= si ottiene: ≤ (
+
≤
= 5.88 ESERCIZIO 2
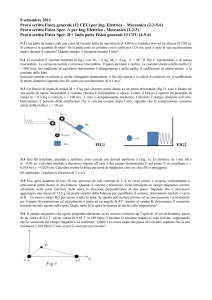
Due punti materiali di uguale massa m = 1 kg, collegati da una sbarretta rigida di
lunghezza d = 0.5 m e massa trascurabile, poggiano in quiete su di un piano privo di
attrito. Una terza massa, identica alle prime due, scivolando sul piano con velocità
v0 = 5 m/s ortogonale alla sbarretta, urta una delle due masse e vi resta saldata.
Calcolare:
a) la velocità del sistema dopo l’urto;
b) la velocità angolare del sistema dopo l’urto;
c) l’energia meccanica che viene dissipata nell’urto.
Soluzione
Il centro di massa del sistema, dopo l’urto, si trova a una distanza
della sbarretta. La distanza da
=
⁄
⁄
=
dal centro
del punto di impatto è: ℎ = ⁄3.
a) La conservazione della quantità di moto fornisce: = 3 , dove
è la velocità del centro di massa
del sistema dopo l’urto. E’:
= ⁄3 = 1.66 .
⁄3 = , con = 2 ( ⁄3) + (2 ⁄3) =
b) La conservazione del momento angolare fornisce: 2⁄3 , dove
è la velocità di rotazione del sistema attorno al c.d.m. dopo l’urto. E’: = ⁄2 =
5
.
c) l’energia meccanica che viene dissipata nell’urto si può calcolare tramite la variazione di energia
cinetica (utilizzando il th. di Koenig):
= 1⁄2 − (1⁄2 3 + 1⁄2 ) = 6.25 ,
quindi il 50% dell’energia iniziale.
1
A.A. 2013-14
Fisica Generale
24-06-14
ESERCIZIO 3
Un cilindro di massa m = 1 kg e raggio R, in moto di puro rotolamento su un piano orizzontale scabro
con velocità v1 = 10 m/s, viene rallentato in modo costante mediante un freno fino a raggiungere la
velocità v2 = 2 m/s in un tempo t = 10 s.
Calcolare la potenza media dissipata.
Soluzione
La potenza dissipata deriva dal lavoro della forza frenante, che si può calcolare tramite il teorema delle
forze vive. L’energia cinetica di un cilindro che rotola è:
= 1⁄2 + 1⁄2
= 1⁄2 +
)( ⁄ ) = 3⁄4 . Quando la velocità varia da v1 = 10 m/s a v2 = 2 m/s, si ha una
1⁄2 (1⁄2
variazione (negativa) di energia cinetica pari a: ∆ = 3⁄4 − 3⁄4 = −72 . Tale perdita di
energia è pari al lavoro svolto solo dalla forza frenante; la potenza è quindi: = ⁄ = 7.2
ESERCIZIO 4
Un gas ideale monoatomico compie un ciclo reversibile, costituito da una espansione isoterma AB,
dove il gas raddoppia il volume, da una isocora BC e da una adiabatica CA.
a) Disegnare il ciclo nel piano di Clapeyron.
b) Calcolare il rendimento del ciclo.
Soluzione
Il calore viene assorbito nella isoterma e ceduto nella isocora. Detta T la
temperatura assoluta dell'isoterma e TC quella dello stato C, si ha
= 1 −
|
|
=1−
)
(
⁄
Per ricavare TC, si osservi che nel ciclo la variazione di entropia è nulla:
∆ =
ln
+
ln
=0→
⁄
= 2
(con VB = 2 VA)
Sostituendo nella equazione precedente si ottiene:
= 1 −
|
|
=1−
⁄
= 0.2
ESERCIZIO 5
Due cariche puntiformi q1= +40 10−9 C e q2 = −30 10−9 C sono ad una distanza d = 10 cm l’una
dall’altra. Il punto A si trova, sulla congiungente le due cariche, a metà distanza, mentre il punto B́ è
sulla congiungente le due cariche, a h = 8 cm da q1. Calcolare:
a) il potenziale nel punto A;
b) il potenziale nel punto B;
c) il lavoro richiesto per trasportare la carica q0= +25 10−9 C dal punto B al punto A.
Soluzione
a) Il potenziale nel punto A è:
=
b) Il potenziale nel punto B è:
=
⁄
+
+
⁄
= 1800
= 3000
c) Per trasportare la carica q0= +25 10−9 C dal punto B al punto A bisogna svolgere un lavoro dato da
= ( − ) = (+25 ∙ 10 )(1800V − 3000V) = −30 ∙ 10 2
A.A. 2013-14
Fisica Generale
24-06-14
ESERCIZIO 6
Una barra di resistenza trascurabile scivola verso destra su due rotaie di resistenza trascurabile separate
da distanza d = 0.45 m. Le rotaie sono collegate da una resistenza R = 12.5 e l’intero sistema è
immerso in un campo magnetico B = 0.750 T uscente dal piano. Calcolare:
a)
b)
c)
d)
la velocità con cui deve muoversi la barra per produrre una corrente i = 0.155 A nella resistenza;
la forza che va applicata alla barra per mantenere la corrente al valore costante i = 0.155 A;
l’energia dissipata dalla resistenza nell’unità di tempo;
la potenza meccanica fornita alla sbarra.
Soluzione
a) La corrente indotta è data dall’espressione =
| |
( )
=
=
, da cui
=
= 5.74 b) La corrente indotta gira in verso tale da creare un campo che si oppone al campo esistente (quindi entrante).
Tale corrente genera, interagendo con detto campo magnetico, una forza diretta in verso opposto alla
velocità. Per mantenere la velocità costante, e quindi la corrente, bisogna quindi applicare una forza uguale e
contraria alla forza prodotta dalla corrente indotta, ovvero
=
=
=
= 0.052
c) L’energia viene dissipata dalla resistenza per effetto Joule. Nell’unità di tempo vale:
=
= 0.3
d) La potenza meccanica fornita alla sbarra è invece: = = 0.3 , ovviamente uguale in modulo alla
potenza dissipata nella resistenza.
3