Teoria dei Circuiti
A.A. 2016/17
27 gennaio 2017
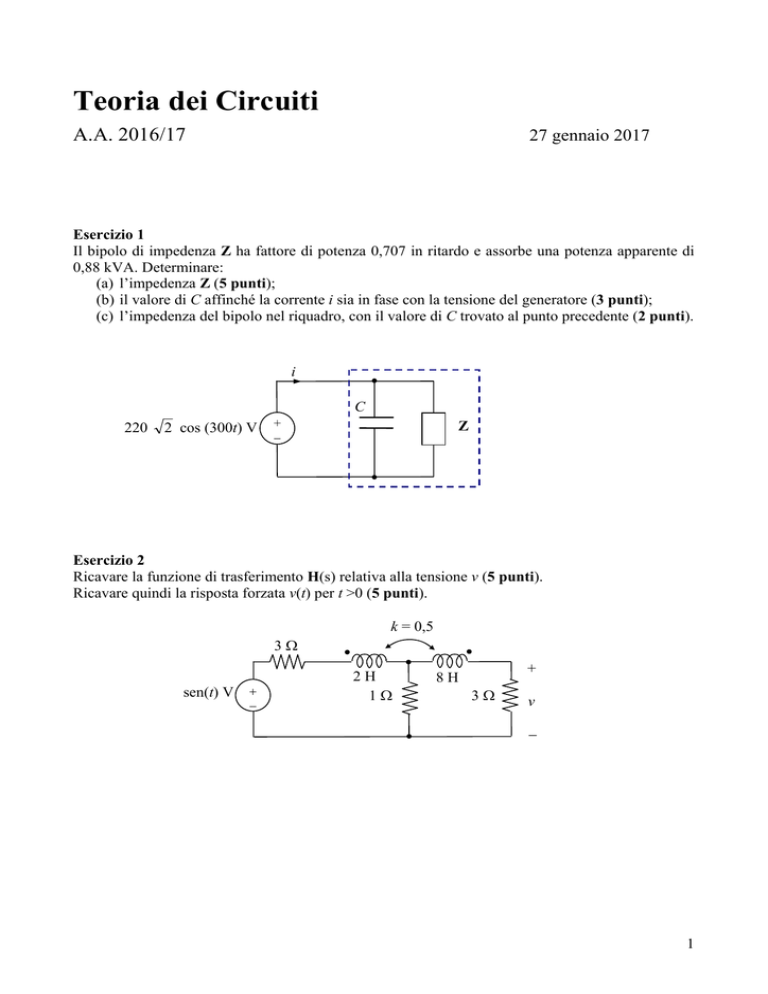
Esercizio 1
Il bipolo di impedenza Z ha fattore di potenza 0,707 in ritardo e assorbe una potenza apparente di
0,88 kVA. Determinare:
(a) l’impedenza Z (5 punti);
(b) il valore di C affinché la corrente i sia in fase con la tensione del generatore (3 punti);
(c) l’impedenza del bipolo nel riquadro, con il valore di C trovato al punto precedente (2 punti).
i
C
220
2 cos (300t) V
+
−
Z
Esercizio 2
Ricavare la funzione di trasferimento H(s) relativa alla tensione v (5 punti).
Ricavare quindi la risposta forzata v(t) per t >0 (5 punti).
k = 0,5
3Ω
sen(t) V
+
−
2H
1Ω
+
8H
3Ω
v
−
1
Domanda 1
Dimostrare il teorema di Millman. (5 punti)
Domanda 2
La tensione del resistore di un circuito RLC serie presenta la risposta in frequenza nella figura
seguente. Ricavare i valori approssimati di L e C sapendo che R = 10 Ω.
(5 punti)
1.0V
0.8V
0.6V
0.4V
0.2V
0V
0Hz
0.5KHz
1.0KHz
1.5KHz
2.0KHz
2.5KHz
3.0KHz
V(R1:2)
Frequency
2
Soluzione Esercizio 1
S = Veff I eff = 880
⇒
I eff = 880 / 220 = 4 A ⇒
Z = Veff / I eff = 55 Ω
Re[Z] = 55 × 0,707 = 38,885 Ω
0,707 = cos(45°)
Y = jωC +
Im[Z] = 55 × 0,707 = 38,885 Ω
⇒
1
= jωC + 0,0128(1 − j )
38,885(1 + j )
⇒ C ≅ 42,86 μF
300 C = 0,0128
Y’ = 0,0128
⇒
Z’ ≅ 78 Ω
Soluzione Esercizio 2
La mutua induttanza è M = 0,5 16 = 2 H. Applicando la trasformazione a T si ottiene il circuito
seguente.
3Ω
6H
+
2H
+
vin
v
−
3Ω
1Ω
−
Il circuito simbolico con condizioni iniziali nulle è mostrato di seguito.
3
1
6s
+
Vin
+
−
2s
V
3
1
−
RIF
Applicando la LKC al nodo 1 si ottiene l’equazione
V1 − Vin
V1
V1
+
+
=0
3
1 + 2s 3 + 6s
Infine
V = V1
la cui soluzione è V1 = Vin
V1
1
3
=
⇒
= Vin
3 + 6s 1 + 2s
5 + 2s
H( s) =
1 + 2s
.
5 + 2s
1
5 + 2s
3
V(s) =
A=
1
A
B
B*
=
+
+
2
2( s + 5 / 2)( s + 1) s + 5 / 2 s − j s + j
2
29
v(t ) =
B=
1
1
∠ - 90° - 21,8°
=
2 j (5 + 2 j ) 2 29
2 − 2 , 5t
1
e
+
sen(t − 21,8°) V.
29
29
Domanda 2
f0 ≅ 800 Hz
Bf ≅ 180 Hz
Q ≅ 800/180 = 4,45
Q = 2πf0 L/R ⇒
2πf0 =
1
LC
⇒
L ≅ 8,85 mH
C ≅ 4,47 μF
4