Document

STUDIO DI FUNZIONI
1) Determinare il dominio della funzione, eventuali peculiarità (parità), andamento del
segno, limiti, eventuali asintoti e intersezioni con gli assi, eventuali discontinuità e loro
classificazione, crescenza e decrescenza, eventuali massimi e minimi
1
y = e x−2
Osserviamo che l’unico punto in cui non è definita la funzione è x = 2, in cui si annulla il
denominatore della frazione all’esponente. Dunque:
D = R − {2}
Risulta inoltre che la funzione non è né pari né dispari.
Passiamo allo studio dei limiti:
lim e
1
x−2
x → +∞
1
∞
+
= e = e0 = 1
1
1
−
lim e x − 2 = e −∞ = e 0 = 1
x → −∞
1
1
lim+ e x − 2 = e 0 = e + ∞ = ∞
+
x →2
lim− e
1
x−2
x →2
1
=e
0−
= e −∞ = 0
Dunque la funzione presenta un asintoto verticale in x = 2 e un asintoto orizzontale y = 1.
In x = 2 la funzione presenta una discontinuità di seconda specie in quanto il limite destro tende a
+∞
Passiamo allo studio della derivata prima. Si ha:
1
y ' = −e x − 2 ⋅
1
( x − 2 )2
Da ciò risulta che la derivata prima è sempre negativa, in quanto entrambi i fattori presenti sono
sempre positivi (per x ≠ 2), ma sono preceduti da un segno negativo. Ne concludiamo che la
funzione è sempre decrescente e non vi sono massimi né minimi stazionari. In quanto al valore 0,
cui tende il limite della funzione per x → 2 da sinistra, osserviamo che esso costituisce un estremo
inferiore ma non un minimo per la funzione.
2) Determinare concavità e flessi e tracciare il grafico della precedente funzione.
Passiamo al calcolo della derivata seconda. Risulta:
−e
1
x−2
y' ' =
⎛
1
⋅ ⎜⎜ −
2
⎝ (x − 2)
1
⎞
⎟ ⋅ ( x − 2 )2 + e x − 2 ⋅ 2 ⋅ ( x − 2 )
1
⎟
2x − 3
⎠
x−2
=
⋅
e
4
( x − 2 )4
(x − 2)
Notiamo che i termini:
e
1
x−2
e
( x − 2 )4
sono sempre positivi (per x ≠ 2), quindi si ha:
y' ' > 0
→ 2x − 3 > 0
→ x>
3
2
La funzione ha quindi concavità negativa per x < 3/2 e positiva per x > 3/2. In x = 3/2 si ha un
flesso obliquo ascendente. A questo punto si può tracciare il grafico della funzione:
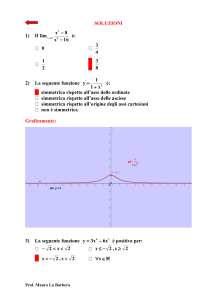
5) Studiare la funzione: y =
x
log x
Iniziamo con l’individuazione del dominio; data la presenza di un logaritmo la funzione è definita
solo per i valori positivi della x; inoltre non si deve annullare il denominatore della frazione. Si ha
quindi:
⎧x > 0
⎨
⎩log x ≠ 0
⎧x > 0
→ ⎨
⎩x ≠ 1
→ D = R + − {1}
Passiamo ora allo studio del segno:
N:x>0
D : log x > 0 → x > 1
Passiamo ora allo studio dei limiti:
Si ha:
∞
x
=
x → ∞ log x
∞
lim
1
x
= lim = lim x = ∞
x →∞ log x
x →∞ 1
x →∞
x
→ lim
1
x
= =∞
x →1 log x
0
0
x
lim
=
=0
x →0 log x
−∞
lim
Notiamo quindi che per x = 1 si ha un asintoto verticale. Non vi sono invece asintoti obliqui
perché risulta:
lim
x →∞
f ( x)
=0
x
Possiamo quindi iniziare a tracciare alcuni elementi del grafico della funzione:
Passiamo ora allo studio della derivata; si ha:
y' =
log x − 1
log 2 x
Si nota che il denominatore è sempre positivo o nullo (in x = 1) quindi la derivata è positiva dove è
positivo il numeratore, ossia per:
log x > 1
→ x>e
L’andamento della funzione è quindi:
quindi la funzione ha un minimo relativo in (e,e).
Studiamo infine la concavità; la derivata seconda della funzione è:
y' ' =
2 − log x
x log 3 x
l’andamento del segno della derivata seconda è:
N : 2 − log x > 0 → x < e 2
D : x log 3 x > 0 → x > 1
⎛ e2
Si ha quindi un flesso obliquo nel punto ⎜⎜ e 2 ,
2
⎝
⎞
⎟⎟
⎠
Possiamo quindi tracciare uno schizzo della funzione:
Per confronto riportiamo il grafico ottenuto con Derive:
lim
x →∞
1
⎛
⎞
⎜1 − e x ⎟ ⋅ x = lim
x →∞
⎝
⎠
1
⎛
⎞
⎜1 − e x ⎟
⎝
⎠=0
1
0
x
Applicando la formula de l’Hopital si ottiene:
1
1
⎛
⎞
⎛ 1 ⎞
⎜1 − e x ⎟
−e x ⋅ ⎜ − 2 ⎟
1
⎝
⎠=
⎝ x ⎠ = −e ∞ = 0
lim
lim
1
1
x →∞
x →∞
− 2
x
x
2 −x
5) Studiare la funzione: y = x e
Osserviamo per prima cosa che il dominio della funzione è tutto R; inoltre la funzione non è né pari
né dispari, in quanto è presente il fattore esponenziale che, appunto, non è né pari né dispari.
Passiamo allo studio del segno. Si vede subito che risulta:
f ( x) = x 2 ⋅ e − x ≥ 0
∀x ∈ R
con
f ( x) = 0
per x = 0
da cui si vede che la funzione passa per l’origine.
Passiamo allo studio dei limiti. Si ha:
lim x 2 ⋅ e − x = ∞ ⋅ 0
x → +∞
Per poter applicare la regola de L’Hôpital occorre riscrivere la funzione come segue:
x2 ∞
=
x → +∞ e x
∞
lim x 2 ⋅ e − x = lim
x → +∞
Si ha quindi:
x2
2x
2
2
= lim x = lim x = = 0
x
x → +∞ e
x → +∞ e
x → +∞ e
∞
lim x 2 ⋅ e − x = lim
x → +∞
Si ha poi:
lim x 2 ⋅ e − x = ∞ ⋅ ∞ = ∞
x → −∞
Possiamo sintetizzare le informazioni fin qui raccolte per tracciare un primo abbozzo del grafico:
Passiamo ora allo studio della derivata della funzione:
(
)
y' = 2 x ⋅ e − x − x 2 e − x = 2 x − x 2 e − x
y' > 0
→
(2 x − x )⋅ e
2
−x
>0
Il fattore esponenziale è sempre positivo, per cui è sufficiente studiare il segno del fattore
quadratico. Risulta:
2x − x 2 > 0
→ 0< x<2
L’andamento della funzione è quindi:
⎛ 4⎞
Si ha quindi un minimo relativo nell’origine e un massimo relativo in ⎜ 2, 2 ⎟
⎝ e ⎠
Passiamo allo studio della derivata seconda:
(
)
(
)
y ' ' = (2 − 2 x ) ⋅ e − x − 2 x − x 2 ⋅ e − x = x 2 − 4 x + 2 ⋅ e − x
Nello studio del segno, ancora una volta possiamo limitarci al termine quadratico, in quanto il
termine esponenziale è sempre positivo.
y' ' > 0
→ x 2 − 4x + 2 > 0
→ x < 2− 2
∨
x > 2+ 2
L’andamento della concavità è quindi:
con flessi per x = 2 ± 2
A questo punto possiamo tracciare lo schizzo della funzione:
Per confronto riportiamo di seguito il grafico della funzione ottenuto con DERIVE
6) Studiare la funzione:
1
y = ex
Osserviamo preliminarmente che la funzione è definita per ogni x diverso da zero ed è sempre
positiva. Da ciò deriva che la funzione è tutta contenuta nel primo e secondo quadrante.
Passiamo al calcolo dei limiti:
1
x
1
+∞
1
x
1
−∞
1
x
0+
1
x
0−
lim e = e
x → +∞
lim e = e
x → −∞
lim e = e
x →0
= e0 = 1
1
x →0 +
lim− e = e
= e0 = 1
= e ∞ = +∞
1
= e −∞ = 0
Possiamo quindi tracciare i primi elementi del grafico:
Passiamo ora allo studio del segno della derivata:
1
⎛ 1 ⎞
y' = e x ⋅ ⎜ − 2 ⎟ > 0
⎝ x ⎠
Osserviamo che, per x diverso da zero, il primo fattore è sempre positivo, mentre il secondo è
sempre negativo. Pertanto il segno della derivata è sempre negativo, ossia la funzione è sempre
decrescente e non presenta punti stazionari.
Passiamo allo studio del segno della derivata seconda:
1
⎛ 1 ⎞ ⎛ 1
y' ' = e x ⋅ ⎜ − 2 ⎟ ⋅ ⎜ − 2
⎝ x ⎠ ⎝ x
1
⎞
⎟+ ex
⎠
⎛ 2 ⎞
⋅⎜ 3 ⎟ > 0
⎝x ⎠
1
x
2 ⎞
⎛ 1
→ e ⎜ 4 + 3⎟>0
x ⎠
⎝x
→
1
x
e
⋅ (1 + 2 x ) > 0
x4
Osserviamo che il primo fattore è sempre positivo per x ≠ 0, pertanto si ottiene:
1 + 2x > 0
→ x>−
1
2
Ne deduciamo che la funzione presenta un flesso ascendente in x = -1/2
Possiamo a questo punto tracciare uno schizzo del grafico della funzione:
3) Determinare il dominio della funzione, eventuali peculiarità (parità), andamento del
segno, limiti, eventuali asintoti e intersezioni con gli assi, eventuali discontinuità e loro
classificazione.
y = x ⋅ e−x
Il dominio della funzione è tutto R.
La funzione non è pari, perché
f (− x) = − x ⋅ e x ≠ f ( x)
e non è neppure dispari, come si verifica subito.
La funzione è ovunque non negativa, perché è il prodotto di due fattori entrambi non negativi; si ha
f(x) = 0 solo per x = 0.
Per lo studio dei limiti conviene riscrivere la funzione come segue:
⎧⎪ x ⋅ e − x per x ≥ 0
f ( x) = ⎨
−x
⎪⎩− x ⋅ e per x < 0
In altre parole dovremo è come se dovessimo studiare DUE funzioni: una valida per x ≥ 0 e l’altra
valida per x < 0. Per x ≥ 0 si ha:
lim+ x ⋅ e − x = 0 ⋅ e 0 = 0
x →0
lim x ⋅ e − x = ∞ ⋅ e −∞ = 0
x → +∞
il secondo limite può essere dedotto osservando che l’esponenziale prevale rispetto a qualunque
potenza, oppure utilizzando la regola de L’Hôpital:
x
x → +∞ e x
lim x ⋅ e − x = lim
x → +∞
H
→
1
=0
x → +∞ e x
lim
La funzione ha quindi, a destra, un asintoto orizzontale corrispondente all’asse x.
per x < 0 si ha invece:
lim− − x ⋅ e − x = 0 ⋅ e 0 = 0
x →0
lim − x ⋅ e − x = ∞ ⋅ e + ∞ = +∞
x → −∞
Osserviamo che a sinistra la funzione non presenta asintoti obliqui a sinistra. Infatti si ha:
m = lim
x → −∞
f ( x)
= lim − e x = −∞
x → −∞
x
La funzione non presenta discontinuità. Data la presenza del valore assoluto, possiamo però
prevedere la presenza di un punto angoloso nell’origine.
Possiamo quindi tracciare un primo schizzo della funzione:
4) Determinare crescenza e decrescenza, eventuali massimi e minimi, concavità e flessi e
tracciare il grafico della precedente funzione.
Passiamo allo studio delle derivate. Nel primo quadrante (x ≥ 0) si ha:
⎧x ⋅ e − x
f ( x) = ⎨
⎩x ≥ 0
→
f ' ( x) = e − x − x ⋅ e − x = (1 − x ) ⋅ e
−x
considerando che il termine esponenziale è sempre positivo, si ricava
f ' ( x) > 0
→ 1− x > 0
→ x <1
⎛ 1⎞
si vede quindi che per x = 1 la funzione presenta un massimo relativo: M ⎜1; ⎟
⎝ e⎠
Concludiamo lo studio della derivata prima osservando che:
lim+ (1 − x) ⋅ e − x = 1
x →0
quindi avvicinandosi a 0 da destra la tangente della funzione ha coefficiente angolare + 1
Passiamo allo studio della derivata seconda. Sempre per x ≥ 0, si ha:
y ' ' = e − x (x − 2)
che risulta positiva per x > 2. La concavità della funzione ha quindi il seguente andamento:
Notiamo che in x = 2 vi è un flesso obliquo discendente
Passiamo ora allo studio delle derivate per x < 0. Per la derivata prima si ha:
⎧− x ⋅ e − x
f ( x) = ⎨
⎩x < 0
→
f ' ( x) = −e − x + x ⋅ e − x = ( x − 1) ⋅ e
−x
da cui:
f ' ( x) > 0
per
x >1
ma poiché deve essere x < 0, ne deduciamo che per x < 0 la funzione è sempre decrescente.
Osserviamo che risulta:
lim ( x − 1) ⋅ e − x = −1
x →0 −
Questo conferma che nell’origine la funzione non è derivabile, in quanto la derivata sinistra tende a
–1 e quella destra a + 1. Poiché la funzione è continua nell’origine, abbiamo quindi un punto
angoloso, che è anche il minimo assoluto.
Passiamo allo studio della derivata seconda:
f ' ' ( x) = e − x (2 − x )
→
f ' ' ( x) > 0
per
x<2
Ne deduciamo che per x < 0 la funzione ha sempre concavità positiva. Possiamo ora tracciare il
grafico della funzione:
PROBLEMI DI MASSIMO E DI MINIMO
Inscrivere nel quadrato di lato L il quadrato di area minima
Il problema può essere schematizzato nella figura seguente:
Rendere minima l’area del quadrato inscritto nel quadrato di lato L, equivale a rendere massima la
somma delle aree dei quattro triangoli rettangoli di cateti rispettivamente x ed L-x , ossia rendere
massima l’espressione:
1
A( x) = 4 ⋅ ⋅ x ⋅ (L − x ) = 2 x ⋅ ( L − x)
2
con le condizioni: 0 < x < L
Passiamo allo studio del segno della derivata:
A' ( x) = 2 L − 4 x > 0
→ x<
L
2
Pertanto la funzione presenta l’andamento raffigurato nello schema seguente:
Ne deduciamo che per x = L/2 la funzione presenta un massimo e quindi il quadrato inscritto ha
l’area minima pari a:
L2 L2
⎛L⎞
L2 − A⎜ ⎟ = L2 −
=
2
2
⎝2⎠
7) Di tutti i triangoli rettangoli aventi assegnata ipotenusa, trovare quello di area
massima.
Consideriamo la figura seguente:
L’area del triangolo è:
A=
1
xy
2
Per il teorema di Pitagora possiamo scrivere:
y = a2 − x2
Sostituendo nella relazione precedente otteniamo un’espressione per l’area come funzione di x:
A( x) =
1
x a2 − x2
2
In base al significato geometrico della misura x della lunghezza del cateto, dobbiamo porre le
condizioni:
x>0
∧
x<a
→ 0< x<a
Passiamo ora allo studio della derivata della funzione:
A' ( x) =
⎤
1⎡ 2
1
a 2 − 2x 2
2
(
)
a
−
x
+
x
⋅
⋅
−
2
x
=
⎢
⎥
2
2
2⎣
2 a2 − x2
⎦ 2 a −x
Osserviamo che il denominatore della frazione dove è definito è sempre non negativo, quindi
possiamo limitarci a studiare il segno del numeratore:
A' ( x) > 0
→ a 2 − 2x > 0
→ −
a
2
< x<+
a
2
L’andamento della funzione può essere dedotto dallo schema seguente:
Osserviamo che la funzione presenta un massimo per x =
a
2
che è un valore compreso
nell’intervallo 0 < x < a.
In corrispondenza di questo valore della x otteniamo per la y:
y = a2 −
a2
a
=
2
2
da ciò deduciamo che il triangolo deve essere isoscele.
8) Determinare un punto sull’asse delle scisse per il quale è minima la somma del
quadrato della sua distanza dalla retta y = x + 1 con il quadrato della sua distanza
dalla retta x = 4.
Tracciamo innanzitutto uno schizzo della costruzione geometrica:
La funzione da minimizzare rappresenta la somma dei quadrati delle distanze del punto P dalla retta
x = 4 e dalla retta y = x + 1.
Assumiamo come incognita la coordinata x del punto. La distanza dalla retta x = 4 sarà
semplicemente:
d1 = 4 − x
Per determinare la distanza dalla retta y = x + 1 riscriviamo l’equazione in forma implicita:
x − y +1 = 0
e ricordiamo la formula che dà la distanza di un punto da una retta:
ax 0 + by 0 + c
d=
a2 + b2
Nel nostro caso la distanza del punto P, che ha coordinate (x,0), dalla retta data è quindi:
d2 =
1⋅ x + 1⋅ 0 + 1
1+1
=
x +1
2
La funzione da minimizzare è quindi:
2
(
x + 1)
y = (4 − x ) +
2
2
→
y=
(
)
1
3x 2 − 14 x + 33
2
La derivata della funzione è:
y' =
6 x − 14
= 3x − 7
2
che si annulla per x = 7/3
La derivata seconda è ovunque positiva, quindi la funzione presenta un minimo in x = 7/3
5) E’ dato un quadrato ABCD di lato di misura a. Trovare sul prolungamento del lato
CD, dalla parte di C, un punto P per cui sia massimo il rapporto AP/BP
Costruiamo per prima cosa la figura:
Assumeremo come incognita l’ascissa del punto P; sono possibili però altre scelte, ad essa
equivalenti.
Con la scelta fatta si ha:
AP = a 2 + x 2
BP = a 2 + ( x − a ) 2
La funzione da massimizzare è il rapporto tra i due segmenti, cioè:
y=
a2 + x2
a 2 + (x − a )
2
Calcoliamo la derivata prima:
[
]
1 a 2 + ( x − a ) 2 2 x ⋅ a 2 + ( x − a) 2 − (a 2 + x 2 ) ⋅ 2( x − a)
y' =
⋅
=
2
2
a2 + x2
a 2 + ( x − a) 2
[
[
]
]
=
a 2 + ( x − a) 2 x ⋅ 2a 2 + x 2 − 2ax − (a 2 + x 2 ) ⋅ ( x − a )
⋅
=
2
a2 + x2
a 2 + ( x − a) 2
=
a 2 + ( x − a) 2 2a 2 x + x 3 − 2ax 2 − a 2 x + a 3 − x 3 + ax 2
⋅
=
2
a2 + x2
a 2 + ( x − a) 2
=
a 2 + ( x − a ) 2 a ⋅ (− x 2 + ax + a 2 )
⋅
2
a2 + x2
a 2 + ( x − a) 2
[
[
[
]
]
]
osserviamo ora, ai fini dello studio del segno, che il radicale quadratico è sempre positivo, come
pure il denominatore del secondo fattore. In definitiva c’è da studiare solo il segno del fattore:
− x 2 + ax + a 2
Si ha quindi:
− x 2 + ax + a 2 > 0
→ x 2 − ax − a 2 < 0
→
(
)
(
a 1− 5
a 1+ 5
<x<
2
2
L’andamento della funzione è rappresentato dallo schema seguente:
Ne deduciamo che la funzione ammette un massimo per x =
(
a 1+ 5
2
)
)