da un'idea della Docente: Rosanna Tupitti
LS Einstein Teramo
Il cartoccio più grande
E' tempo di castagne: agli angoli delle strade ci vengono offerte dai venditori ambulanti con
improvvisati cartocci fumanti! Anche Alice ed Elena mentre passeggiano nel parco sono attratte dal loro
irresistibile profumo! Si avvicinano al chioschetto per acquistarne un pò, ma il il venditore ha terminato
i fogli di carta per fare i cartocci. Alice allora tira fuori dalla sua borsa due dischi uguali di cartoncino
con raggio 20cm e del nastro adesivo. Poichè sono brave in matematica decidono di costruire due
cartocci uguali con la massima capienza possibile. Ritagliano da ciascun disco un settore della stessa
ampiezza accostano i due raggi lungo i quali sono stati fatti i tagli e fissano il tutto col nastro adesivo.
Calcolare l'ampiezza che devono avere i settori ritagliati affinchè il volume dei cartocci così costruiti sia
il massimo possibile.
Soluzione
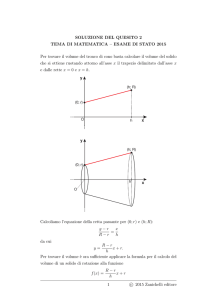
Indichiamo con x (in radianti) l'ampiezza del settore AOB da rimuovere, con R=20cm il raggio del
disco e con l la lunghezza dell'arco AB.
Risulta:
Per costruire il cartoccio rimuoviamo dal disco il settore AOB, accostiamo i raggi OA e OB
ottenendo un cono privato della base.
Calcoliamo il raggio r =HA della circonferenza di base di tale cono di apotema OA=R.
Sapendo che:
ricaviamo, in funzione di x, tale raggio:
(1.1)
dunque
(1.2)
Calcoliamo ora l'altezza del cono:
(1.3)
(1.4)
Dalla formula del volume del cono:
otteniamo l'espressione del volume richiesto:
e sostituendo i valori precedentemente trovati per r ed OH otteniamo:
(1.5)
Calcoliamo ora la derivata della funzione trovata (applicherai la regola di derivazione per un
prodotto):
(1.6)
Studiamo il segno della derivata prima, cercando i valori di x che la rendono positiva:
(1.7)
Valutiamo quale x (in radianti) rende max la funzione:
1.152985986
(1.8)
Valore in gradi dell'angolo che rende massimo il volume:
(1.9)
Concludiamo che rimuovendo un settore di ampiezza circa 66 gradi avremo il cono di volume
massimo.