Soluzione del Quesito 2 - MATutor

SOLUZIONE DEL QUESITO 2
TEMA DI MATEMATICA – ESAME DI STATO 2015
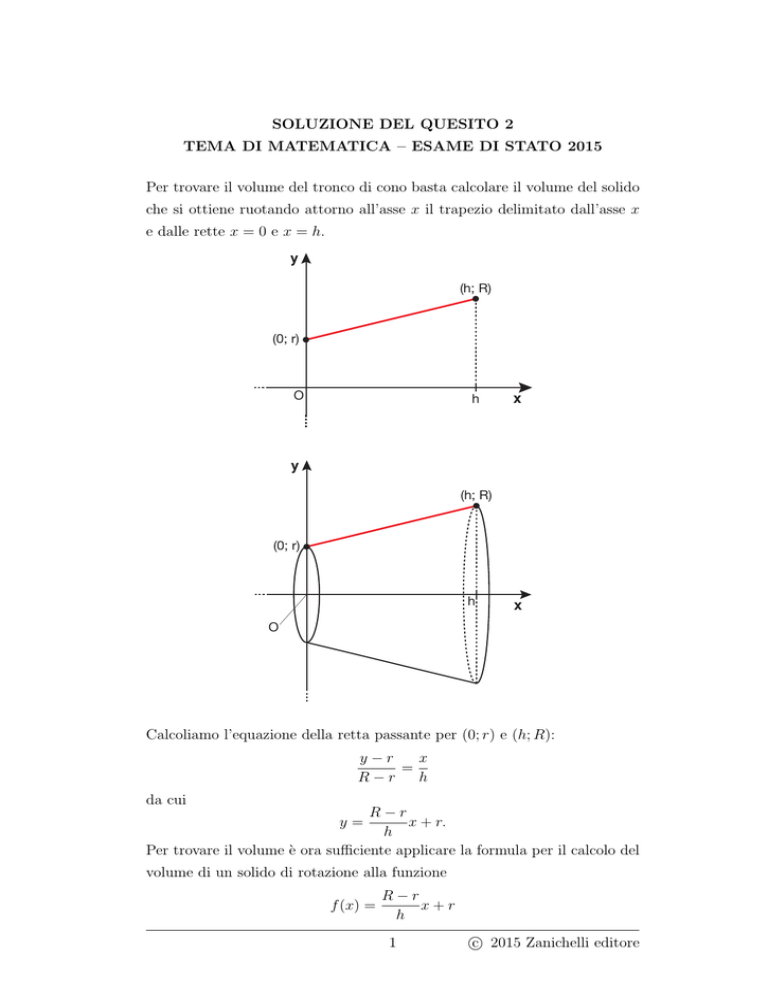
Per trovare il volume del tronco di cono basta calcolare il volume del solido
che si ottiene ruotando attorno all’asse x il trapezio delimitato dall’asse x
e dalle rette x = 0 e x = h.
y
(h; R)
(0; r)
O
h
x
y
(h; R)
(0; r)
h
x
O
Calcoliamo l’equazione della retta passante per (0; r) e (h; R):
y−r
x
=
R−r
h
da cui
R−r
x + r.
h
Per trovare il volume è ora sufficiente applicare la formula per il calcolo del
y=
volume di un solido di rotazione alla funzione
f (x) =
R−r
x+r
h
1
c 2015 Zanichelli editore
nell’intervallo [0; h]:
V
= π
Z h
R−r
0
h
2
x+r
dx = π
Z h"
(R − r)2
h2
0
(R − r)2 3 r(R − r) 2
x + r2 x
= π
x +
3h2
h
"
r(R − r)
x + r2
x +2
h
2
#
dx
#h
0
(R − r)2
= π
h + r(R − r)h + r2 h
3
!
R2 − 2R · r + r2 + 3R · r − 3r2 + 3r2
= πh
3
1
π · h · (R2 + r2 + R · r).
=
3
"
#
Possiamo rispondere alla domanda anche ragionando da un punto di vista
geometrico. Pensiamo al nostro solido come a un cono a cui è stato tolto
un pezzo (sempre un cono) in alto.
V
_
h
B
r
H'
h
A
H
R
I triangoli AHV e BH 0 V sono simili perché sono rettangoli e hanno un
angolo in comune. Quindi si ha
R : (h + h̄) = r : h̄,
da cui si ricava
r
.
R−r
Il volume del tronco di cono si può ottenere sottraendo dal volume del cono
h̄ = h
grande il volume del cono piccolo. Abbiamo quindi
V
πR2 (h + h̄) πr2 h̄
−
=
3
" 3
#
π
rh
rh 2
2
2
=
hR +
R −
r =
3
R−r
R−r
"
#
π
rh
2
2
2
=
hR +
(R − r ) =
3
R−r
=
2
c 2015 Zanichelli editore
i
πh 2
hR + rh(R + r) =
3
π 2
=
h R + r2 + R · r .
3
=
3
c 2015 Zanichelli editore