Una palla di cannone di massa 10 kg viene lanciata con una energia
cinetica di 1000 J. La palla può scavalcare un muro alto 12 m? a)
sicuramente si b) sicuramente no c) potrebbe.., dipende da... E se la
massa della palla fosse di 5 kg?
A
y
h
V0
x
d
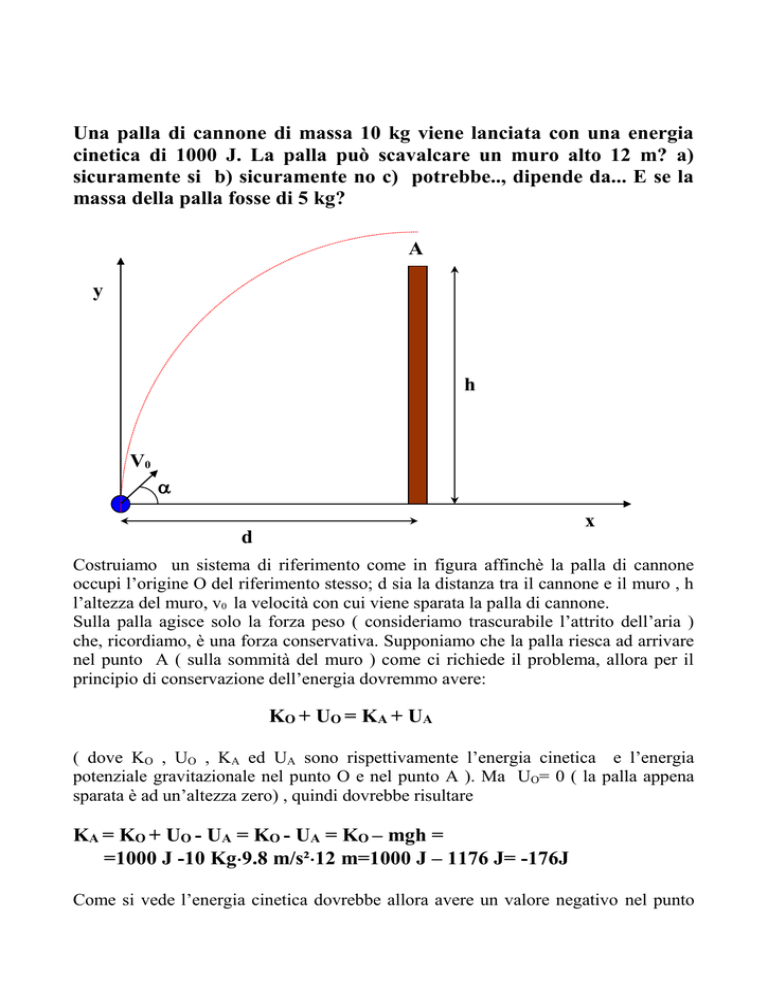
Costruiamo un sistema di riferimento come in figura affinchè la palla di cannone
occupi l’origine O del riferimento stesso; d sia la distanza tra il cannone e il muro , h
l’altezza del muro, v0 la velocità con cui viene sparata la palla di cannone.
Sulla palla agisce solo la forza peso ( consideriamo trascurabile l’attrito dell’aria )
che, ricordiamo, è una forza conservativa. Supponiamo che la palla riesca ad arrivare
nel punto A ( sulla sommità del muro ) come ci richiede il problema, allora per il
principio di conservazione dell’energia dovremmo avere:
KO + UO = KA + UA
( dove KO , UO , KA ed UA sono rispettivamente l’energia cinetica e l’energia
potenziale gravitazionale nel punto O e nel punto A ). Ma UO= 0 ( la palla appena
sparata è ad un’altezza zero) , quindi dovrebbe risultare
KA = KO + UO - UA = KO - UA = KO – mgh =
=1000 J -10 Kg9.8 m/s²12 m=1000 J – 1176 J= -176J
Come si vede l’energia cinetica dovrebbe allora avere un valore negativo nel punto
A, che è impossibile. E’ evidente allora che la palla non può arrivare alla sommità del
muro in nessun caso, indipendentemente da dove sono posizionati il muro ed il
cannone.
Se però facciamo lo stesso calcolo con la massa della palla di cannone pari a 5 Kg
otteniamo:
KA = KO + UO - UA = KO - UA = KO – mgh =
= 1000 J – 5 Kg9.8 m/s²12 m=1000 J – 588 J= 412 J
In questo caso, l’energia cinetica nel punto A risulta positiva e quindi la palla di
cannone potrebbe anche arrivare nel punto A. Per vedere se effettivamente riesce a
raggiungere la cima del muro dobbiamo fare delle ulteriori considerazioni.
La palla è soggetta solo ad una forza verticale ( lungo la direzione dell’asse y ma in
verso opposto a questo ) che è la forza gravitazionale.Quindi il moto lungo l’asse x è
un moto con velocità costante, cioè quella iniziale lungo lo stesso asse
vx = v0x = v0 cos
Al contrario il moto della palla lungo l’asse y è un moto con accelerazione costante
che è l’accelerazione di gravità:
aY = - g = - 9.8 m/s²
Siamo quindi in grado di scrivere, ricordando le formule della cinematica del moto
rettilineo uniforme e del moto uniformemente accelerato:
x = v0x t = v0 cos t
y = v0Y t + ½ aY t² = v0 sen t - ½ g t²
t = x / ( v0 cos )
y = v0 sen t - ½ g t²
sostituendo la prima nella seconda otteniamo
2
v sen
1
x
1
g
2
tg x
yx 0
x g
x
v0 cos
2 v0 cos
2 v0 2 cos 2
Il moto della palla risulta allora parabolico (una parabola con la concavità verso il
basso) come è rappresentato con la linea trattegiata rossa del disegno. Affinchè la
palla riesca ad oltrepassare il muro occorre che la sua ordinata y calcolata nel punto
in cui la palla ha la stessa ascissa del muro (x = d) sia maggiore dell’altezza del muro:
y x d tg d
1
g
2
d
h
2
2
2 v0 cos
Soltanto se d , h , e v0 soddisfano quest’ultima relazione la palla riesce ad
oltrepassare il muro.












