Concetti da introdurre (Cap. 6, §4-10)
♦
♦
♦
♦
♦
Lavoro di una forza
Energia cinetica, Energia potenziale, Energia meccanica
Teorema dell’energia cinetica
Teorema conservazione dell’energia meccanica
Casi di non conservazione dell’energia meccanica
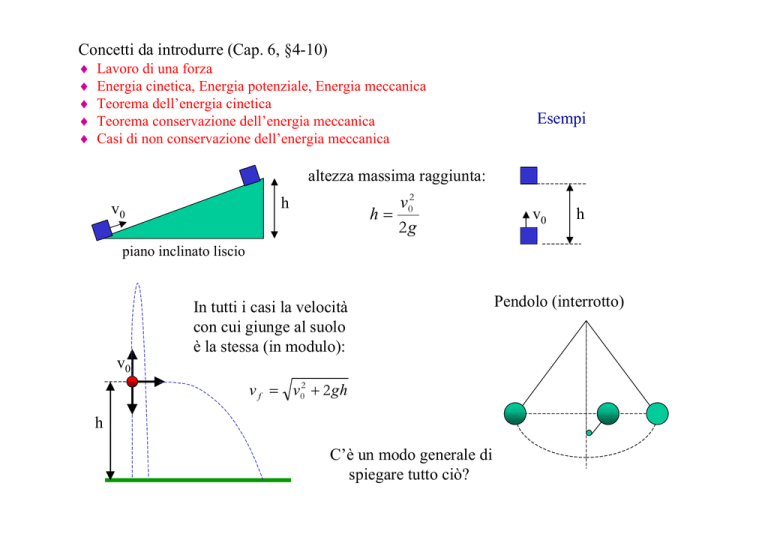
Esempi
altezza massima raggiunta:
v02
h=
2g
h
v0
v0
h
piano inclinato liscio
In tutti i casi la velocità
con cui giunge al suolo
è la stessa (in modulo):
v0
v f = v02 + 2 gh
h
C’è un modo generale di
spiegare tutto ciò?
Pendolo (interrotto)
Lavoro di una forza
1°caso: Forza costante. Spostamento rettilineo.
Il punto di applicazione di F si sposta lungo AB.
r
F
prodotto scalare
θ
r
s
A
0
0
0
0
90
>
⇔
<
θ
<
/
lavoro motore
lavoro resistente / < 0
B
grandezza scalare
r
F
⇔ 90 0 < θ < 1800
lavoro nullo / = 0 ⇔ θ = 90 0
Unità di misura: J = Nm = kg m2/s2
2° caso: Forza costante. Spostamento non rettilineo.
A
B
C
r
r r
/ = F ⋅ AB = F ⋅ s = Fs cos θ
D
r
r
r
/ = F ⋅ AC + F ⋅ CD + F ⋅ DB
r
/ = F ⋅ AC + CD + DB = F ⋅ AB
(
)
Forza costante. Spostamento generico.
Il lavoro di una forza costante
non dipende dal tragitto
r
F
/ = F ⋅ AB
A
B
Lavoro di una forza variabile.
r
r
r
/ = F AC ⋅ AC + FCD ⋅ CD + FDB ⋅ DB
r
r
/ = ∑ F k ⋅ ∆ s k = ∑ F k ∆ s k cos θ k
k
r
F
θ
C
B
r
F CD
A
k
A
r
ds
r
F AC
D
B
r
F DB
Caso generale.
r r
/ = ∫ F ⋅ ds =
B
A,l
B
∫ F cos θ ds
A,l
Il lavoro in generale dipende dal tragitto. Integrale di linea.
Semplici esempi di lavoro. (caso 1D, forza costante)
piano orizz.
liscio
F
F
A
B
s
/ = F ⋅ AB = Fs
piano orizz.
liscio
F
A
v 2f − vi2
2a
a=F m
m
m
m
= s ⇒ Fs = / = v 2f − vi2 = ∆ v 2
2
2
2
Energia cinetica (K)
F
θ
Come varia la velocità?
/ = F ⋅ AB = Fs cos θ
a = F cos θ m
B
s
v 2f − vi2
2a
m
m
m
= s ⇒ Fs cosθ = / = v 2f − vi2 = ∆ v 2
2
2
2
Teorema dell’energia cinetica:
/ = ∆K
Sono casi particolari del
Detto anche:
•Teorema lavoro-energia
•Teorema delle forze vive
[K]=kg m2/s2 = J
L’energia cinetica è una grandezza scalare
Per un punto materiale si definisce energia cinetica: K =
Per un sistema di punti materiali
K=
m
m1 2 m2 2
v1 +
v2 + K + n vn2
2
2
2
I 2
=
ω
K
Per un corpo rigido con asse fisso:
2
In presenza di più forze:
(non ne faremo uso)
∆K = LTOT = L1 + L2 + K
Energia: capacità di compiere lavoro.
m 2
v
2
Lavoro delle altre forze
negli esempi precedenti?
La massa m con velocità
iniziale v è fermata dalla
molla. M compie lavoro
sulla molla.
Lavoro fatto dalla molla?
Anche in questo caso la massa in movimento
ha compiuto lavoro. A spese dell’energia cinetica
Esempio
a = (F − mg sin θ ) m
F
h
s
mgsinθ
v 2f − vi2
2a
= s ⇒ Fs − mgh = ∆K
piano inclinato liscio
/)
/3
Il lavoro per unità di tempo si dice potenza.
potenza
P =
/
∆t
potenza media
r r
r
r
d/
ds
P=
=F⋅
= F ⋅v
dt
dt
si misura in Watt: W = J/s = kg m2/s3
potenza istantanea
Esempio. Auto (m=1400kg) accelera da 0 a 100km/h in 8s. Determinare la potenza media erogata
e la potenza istantanea massima nell’ipotesi che l’accelerazione sia costante.
P =
L ∆K
=
≅ 67.5kW
∆t
∆t
PMAX = Fv MAX = mav MAX = 135kW
Esempi di Lavoro
Forza peso
r
d s
dy
B
h
A
r
m g
mg
alternativamente, poiché la forza è costante:
r
/ = mg ⋅ AB
La forza peso è un caso particolare della
d/ = 0
Forza gravitazionale
r
r1
F1
r
r2
F2
O
dx
d/ = −mg ⋅ dy ⇒
/ = −mg∆y = −mgh
Dipende solo dai
punti A e B.
r
r
d / = − FG ⋅ d r ⇒
m1m 2
d/ = −G
dr
2
r
1 1
/ = Gm1 m2 −
r1 r2
Esempi di Lavoro.
Forza elastica.
d / = − kx ⋅ dx ⇒
/ = k (x 12 − x 22 ) 2
x
FEL
Dipende solo dai
punti estremi.
Fext
Negli esempi precedenti /AB dipende solo dai punti A e B, non dipende dalla linea seguita.
Non è sempre così:
Attrito dinamico
d/ = − AS ⋅ dl ⇒
A
B
/ = − AS ⋅ l AB
Forze che non compiono lavoro
Perché sono normali agli spostamenti:
Reazione normale, Forza di Lorentz (v.)
Perché non c’è spostamento:
Attrito statico, vincoli vari ...
Perché la somma dei lavori è nulla: Tensione di un filo (in certi casi)
Forze conservative
/AB ,γ = /AB ,η = /AB
Il lavoro di alcune forze non dipende dal tragitto ma solo dal punto iniziale e finale.
γ
si dicono Forze Conservative.
Conservative Altra def.:
Il lavoro lungo un percorso chiuso è nullo.
B
η
A
E’ più corretto parlare di campi di forza, nel senso che ad ogni posizione corrisponde
una forza. Le forze conservative dipendono solo dalla posizione.
Con forze conservative, ad ogni posizione si associa una capacità di compiere lavoro e
quindi una energia posizionale.
Si può sfruttare la posizione iniziale di m per accelerare M
m
M
h
Si definisce l’ Energia Potenziale (o posizionale) W
in modo che:
/AB = WA − WB = −(WB − WA ) = −∆W
[W]=[/]=J
Energia Potenziale
Dal confronto delle espressioni calcolate per il lavoro si ricava:
W = mgy
+ cost.
Gm 1 m 2
W =−
+cost.
r
W =
k
x
2
2
+cost.
Forza peso (y: posizione lungo l’asse verticale)
di solito si pone cost=0 (W rispetto ad un livello di riferimento)
Forza di gravitazione universale (r distanza fra le masse)
di solito si pone cost=0 (W nulla a distanza infinita)
Forza elastica (x: deformazione della molla)
di solito si pone cost=0 (W nulla se la molla è a riposo)
definite a meno di
una costante arbitraria.
arbitraria
Es. lavoro della forza peso nella caduta.
h2
h1
h1+h2=h
L = − ∆ W = mg (y i − y f ) = mgh
il risultato non dipende dalla scelta del riferimento
Teorema di conservazione dell’energia meccanica
In presenza di sole forze conservative
/ = ∆E K
⇒ ∆E K = −∆W
/ = −∆W
K F − K I = WI −WF
K I + WI = K F + WF = E
Energia meccanica
La somma delle 2 “capacità di compiere lavoro” si chiama energia meccanica
(“meccanica” perché non è l’energia totale: manca l’energia interna)
vi=0, y=h
E
W
K
y
vf, y=0
compressione max.
K=0, W=max
posiz. riposo.
K=max, W=0
allungamento max.
K=0, W=max
Energia meccanica in presenza di forze non conservative
/ = /C + /N = /N − ∆ W
/ = ∆E K
⇒
∆ (W + K ) = ∆ E = /N
Variazione di energia meccanica
Es. 1. Forza di attrito dinamico
In questo caso LN=LA<0
l’energia meccanica diminuisce
piano inclinato con attrito
Es. 2. Forza applicata per mezzo di una fune
In questo caso l’energia può aumentare
o diminuire.
Conservazione dell’energia meccanica
Esempi. Forza peso.
Proiettile lanciato verso l’alto. Altezza massima.
Ei = K i + Wi =
v0
Ef = K
f
+Wf
m 2
v0 + 0
m 2
2
v 0 = mgh
⇒
2
= 0 + mgh
E i = K i + W i = 0 − mg l cos θ
Ef = K
⇒
f
+Wf =
m 2
v max
2
− mg l
m 2
v max = mg l ( 1 − cos θ )
2
v=0
Pendolo.
vMAX
v
v0
Piano inclinato liscio.
θ
h
Moto parabolico di un proiettile.
Conservazione dell’energia meccanica
Esempi
v0
Molla ideale sospesa.
Forza elastica e forza peso.
Molla ideale di costante k.
Piano orizzontale liscio.
Forza gravitazionale. Orbita di un pianeta.
Forza gravitazionale. Velocità di fuga.
Caso di forze conservative e non conservative.
Piano inclinato con attrito.












