La Parabola
Di cosa si tratta?
Una parabola può essere
definita come luogo
geometrico nel modo
seguente:
• Una parabola è l'insieme
dei punti del piano
equidistanti una retta r
(detta direttrice) e da un
punto F (detto fuoco) non
contenuto in r.
Galileo e la Parabola
Galileo per primo dimostrò
che la traiettoria descritta
da un proiettile è un arco
di parabola.
Nell’introduzione alla terza
giornata dei Discorsi egli
scrive:
“Nulla v'è, forse, di più antico del moto, e su di esso ci sono non pochi
volumi, né di piccola mole, scritti dai filosofi; tuttavia tra le sue proprietà
ne trovo molte che, pur degne di essere conosciute, non sono mai state
finora osservate, nonché dimostrate.
[ ... ] E' stato osservato che i corpi lanciati, ovverosia i proietti,
descrivono una linea curva di un qualche tipo; però, che essa sia una
parabola, nessuno l'ha mostrato. Che sia cosi, lo dimostrerò insieme ad
altre non poche cose, né meno degne di essere conosciute, […] .”
Come si pensavano dunque queste “linee curve”?
Prima che Galileo giungesse
ad una dimostrazione del
moto parabolico dei
proiettili, queste cadute,
come lui stesso ci
testimonia insieme alla
foto adiacente, erano
pensate come “linee
curve” , ovvero,
caratterizzate da una
ascesa rapida e
sostanzialmente lineare e
da una caduta verticale
attraverso un angolo a
gomito.
La disputa del brevetto
In realtà l'enunciazione e la dimostrazione del moto parabolico dei proiettili
venne pubblicata per la prima volta dal Cavalieri nel 1632 nel libro
Specchio ustorio, attestando però in una lettera allo stesso Galileo di
haver imparato in gran parte da lei ciò ch 'io tocco in questa materia.
Galileo ne rimase molto amareggiato e in una lettera del settembre 1632
scriveva:
lo non posso nascondere tale avviso essermi stato di poco gusto, nel
vedere come di un mio studio di più di 40 anni mi deva esser levato
allle primizie, e sfiorata quella gloria che tanto avidamente desideravo
e mi promettevo da si lunghe fatiche; perché veramente il mio primo
intendimento, che mi mosse a specular sopra 'l moto, fu il ritrovar tal
linea, la quale se ben ritrovata, è poi di non molto difficile
dimostrazione.
Lo strumento
Con questo strumento, di grande
efficacia didattica, si può verificare
la legge di composizione dei moti
della cinematica del punto
materiale, qui approssimato con
una piccola biglia di metallo. In
particolare si ha l'immediato
riscontro visivo che un corpo
soggetto all'accelerazione di gravità
e scagliato in avanti con una certa
velocità descrive, cadendo a terra,
un tratto di parabola appartenente
al piano individuato dai due vettori
(velocità e accelerazione di
gravità) che caratterizzano il suo
moto .
Quali sono le componenti dello strumento?
Lo strumento si compone di pochi ma essenziali
elementi:
• La rampa, dove la biglia potrà incrementare la
sua velocità,
• Il compensato sul quale è tracciata la parabola
ideale che la nostra pallina dovrà seguire in linea
di massima,
• Gli anelli, fissati nel compensato, consentono
anche a chi non dispone di attrezzi sofisticati di
determinare la traiettoria della biglia,
• La fossetta d’arrivo, dove terminerà la corsa
della pallina e di conseguenza il nostro
esperimento.
L’esperimento
La rincorsa
Lo stacco
Il volo
L’atterraggio
La spiegazione fisica…
Manovrando il dispositivo di rilascio della biglia, essa percorre lo scivolo
incrementando gradualmente la propria velocità. Quindi, non appena la
biglia lascia lo scivolo con una certa velocità (con direzione parallela al
suolo per costruzione), essa si troverà soggetta all'accelerazione di gravità:
il piano di traiettoria risulta dunque perpendicolare al suolo. Ora si immagini
un piano cartesiano con vertice posizionato in corrispondenza della fine
dello scivolo, asse delle y orientato verso il basso e asse delle x orientato
nel senso del moto. Per studiare la traiettoria della biglia si analizzano i due
moti indipendenti lungo gli assi del sistema di riferimento scelto e
precisamente:
•
•
il moto rettilineo uniforme lungo x di equazione x = v0t, in cui t è il tempo
e v0 la velocità lungo x di distacco della biglia (velocità che si mantiene
costante fino all'arrivo al suolo);
il moto uniformemente accelerato verso il basso di equazione y = ½ gt2,
con g l'accelerazione di gravità che, in una regione ristretta della superficie
terrestre, si può considerare con buona approssimazione costante durante il
moto in direzione e modulo (è evidente che in questo ragionamento non si
tiene conto della resistenza dell'aria, altrimenti la funzione sarebbe diversa).
Per avere l'equazione della traiettoria è sufficiente a questo punto esprimere y
in funzione di x: ciò che si ottiene è l'equazione y = gx2/(2v02) che
rappresenta una parabola, come volevasi dimostrare.
…ed alcune piccole problematiche
•
•
•
•
Gli anelli di controllo della traiettoria sono leggermente più grandi delle
dimensioni della biglia e questo perché il suo moto di caduta è disturbato da
vari fattori:
la non perfetta perpendicolarità dello strumento;
la resistenza dell'aria atmosferica che distorce leggermente la traiettoria;
l'attrito che la biglia subisce ad opera del contatto col precedente tratto di
guida, che incide sulla velocità al momento del distacco (essa non è mai
uguale, ma sempre leggermente diversa caduta per caduta);
gli urti della pallina sulle guide laterali, che modificano la direzione del
vettore velocità al momento del distacco (essi comportano un piccolissimo e
imprevedibile spostamento laterale di direzione perpendicolare al piano su
cui giace la traiettoria di caduta della biglia.
Per tutte queste cause di disturbo la traiettoria della pallina non si può
descrivere con una "curva di traiettoria" (propria del caso ideale), ma
attraverso un "tubo cilindrico di traiettoria" di forma parabolica di cui gli
anelli di controllo ne segnano a intervalli la superficie ideale. La biglia è
dunque libera di percorrere qualsiasi traiettoria che stia all'interno del "tubo
cilindrico" la cui curva di traiettoria ne è l'asse.
Lo strumento è purtroppo danneggiato: l'evidente frattura nel legno ha spostato
l’asse dello strumento poggiante su tre soli pioli, il che fa cadere alle volte la
biglia al di fuori del punto d'arrivo previsto.
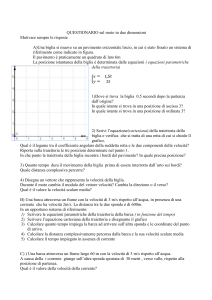
Calcoliamo ora questo moto parabolico
Fisicamente
x = v0t ; y = gt2/2
t = x/v0
y = gx2/2v02
g/2v02 = k = 0,0234
(trovato
algebricamente dalla tabella)
g = 9,8 m/s
2
v0 = 1,44 m/s
Algebricamente
y = kx2
sostituisco y e x con dei valori
della tabella
(x = 48; y = 54)
y = kx2 54 = k 2304
y = gx2/2v02
2v02 = 2304g/54 = 41.880
v0 = 1,44 m/s