NECESSITÀ DEI LOGARITMI
Nelle equazioni esponenziali che abbiamo risolto sinora era sempre possibile ridursi a equazioni in cui si
aveva la stessa base, l’equazione diventava algebrica semplicemente uguagliando gli esponenti. Ma non
tutte le equazioni sono esponenziali sono riducibili, nei casi non riducibili è necessario introdurre il
concetto di logaritmo.
Un semplice esempio di equazione non riducibile è il seguente: 2 x = 5
Cosa possiamo dire della soluzione di quest’equazione? 5 non è una potenza diretta di 2 , però dato che
2 2 < 5 < 2 3 possiamo dire che sarà 2 2 < 2 x < 2 3 e quindi che 2 < x < 3
Quindi avremo x = 2 ,.... in cui conosciamo almeno la parte intera.
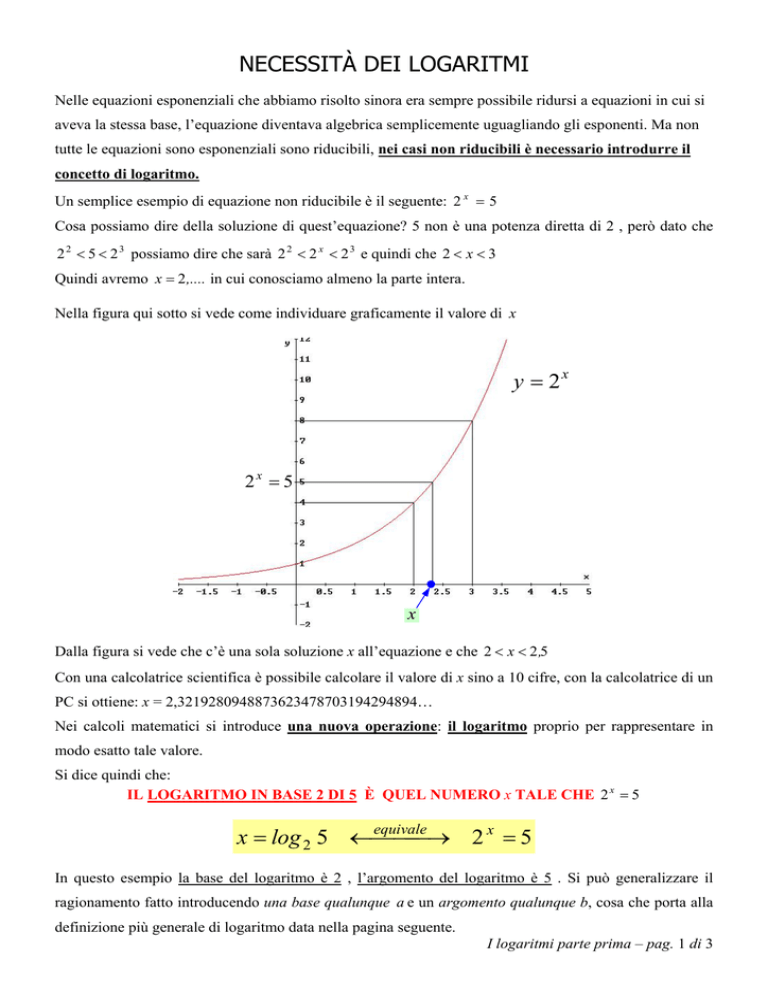
Nella figura qui sotto si vede come individuare graficamente il valore di x
y = 2x
2x = 5
x
Dalla figura si vede che c’è una sola soluzione x all’equazione e che 2 < x < 2 ,5
Con una calcolatrice scientifica è possibile calcolare il valore di x sino a 10 cifre, con la calcolatrice di un
PC si ottiene: x = 2,3219280948873623478703194294894…
Nei calcoli matematici si introduce una nuova operazione: il logaritmo proprio per rappresentare in
modo esatto tale valore.
Si dice quindi che:
IL LOGARITMO IN BASE 2 DI 5 È QUEL NUMERO x TALE CHE 2 x = 5
equivale
x = log 2 5 ←
→ 2 x = 5
In questo esempio la base del logaritmo è 2 , l’argomento del logaritmo è 5 . Si può generalizzare il
ragionamento fatto introducendo una base qualunque a e un argomento qualunque b, cosa che porta alla
definizione più generale di logaritmo data nella pagina seguente.
I logaritmi parte prima – pag. 1 di 3
DEFINIZIONE DI LOGARITMO
IL LOGARITMO IN BASE a DI b
x
È QUEL NUMERO x TALE CHE a = b
equivale
x = log a b ←
→ a x = b
La base a deve soddisfare alle condizioni 0 < a < 1 ∨ a > 1
L’argomento b deve soddisfare la condizione b > 0
………………………………………………………………………………………………………………
Dalla definizione data dovrebbe essere chiaro che il logaritmo è un esponente. Alcuni logaritmi possono
essere calcolati semplicemente passando dalla equazione logaritmica a quella esponenziale.
Esempi:
x = log 3 9 → 3 x = 9 → 3 x = 32
→
x=2
Possiamo quindi dire che log 3 9 = 2 , dato che 32 = 9
………………………………………………………………………………………………………………
1
1
x = log 5
→ 5x =
→ 5 x = 5 − 2 → x = −2
25
25
1
1
Quindi log 5
= −2 , dato che 5−2 =
25
25
………………………………………………………………………………………………………………
3
x = log 6 5 216
→ 6 x = 5 216
→ 6 x = 5 63
→
6x = 65
→
x=
3
5
3
3
, dato che 6 5 = 5 216
5
………………………………………………………………………………………………………………
Quindi log 6 5 216 =
Esercizi per lo studente diligente:
sul libro di testo pag. 71
o numeri 24-25-26-27
o numeri 33-34-35-36-37
o numeri 41-42-43-44
………………………………………………………………………………………………………………
I logaritmi parte prima – pag. 2 di 3
PRIME PROPRIETÀ DEI LOGARITMI
Dalla definizione di logaritmo seguono immediatamente le proprietà seguenti, da
ricordare a memoria.
………………………………………………………………………………………………………………
1a PROPRIETÀ DEI LOGARITMI
log a 1 = 0
DIMOSTRAZIONE
x = log a 1 → a x = 1 → a x = a 0
→
x=0
ossia
log a 1 = 0
QED♦
………………………………………………………………………………………………………………
2a PROPRIETÀ DEI LOGARITMI
loga a = 1
DIMOSTRAZIONE
x = log a a → a x = a → a x = a 1
→
x =1
ossia
log a a = 1
QED
………………………………………………………………………………………………………………
3a PROPRIETÀ DEI LOGARITMI
loga a n = n
DIMOSTRAZIONE
x = log a a n
→ ax = an
→ a x = an
→
x=n
ossia
log a a n = n
QED
………………………………………………………………………………………………………………
♦
Quod Erat Demonstrandum
I logaritmi parte prima – pag. 3 di 3
ALTRE PROPRIETÀ DEI LOGARITMI
I logaritmi hanno altre proprietà importanti (che vanno memorizzate).
4a PROPRIETÀ DEI LOGARITMI
LOGARITMO DI UN PRODOTTO
loga bc = loga b + loga c
Il logaritmo di un prodotto è uguale alla somma dei logaritmi dei singoli fattori.
DIMOSTRAZIONE
Poniamo:
x = log a b
Allora avremo:
x = log a b → a x = b
Quindi:
e
y = log a c
e y = log a c → a y = c
log a bc = log a a x a y = log a a x + y = x + y = loga b + loga c
QED
………………………………………………………………………………………………………………
5a PROPRIETÀ DEI LOGARITMI
LOGARITMO DI UN RAPPORTO
b
loga = loga b − loga c
c
Il logaritmo di un prodotto è uguale alla differenza dei logaritmi dei singoli fattori.
DIMOSTRAZIONE
Poniamo:
x = log a b
Allora avremo:
x = log a b → a x = b
Quindi:
log a
e
y = log a c
e y = log a c → a y = c
b
ax
= = log a y = log a a x − y = x − y = log a b − log a c
c
a
QED
………………………………………………………………………………………………………………
Le proprietà 4 e 5 esprimono le proprietà delle potenze nel caso del prodotto e del rapporto. Ricordando
che i logaritmi sono degli esponenti, quelle sono appunto le proprietà degli esponenti.
………………………………………………………………………………………………………………
Esempi:
log a 15 = log a 5 ⋅ 3 = log a 5 + log a 3
log a
5
= log a 5 − log a 3
3
I logaritmi parte seconda – pag. 1 di 2
6a PROPRIETÀ DEI LOGARITMI
LOGARITMO DI UNA POTENZA
loga bn = n ⋅ loga b
Il logaritmo di una potenza è uguale all’esponente della potenza moltiplicato per il logaritmo della base
DIMOSTRAZIONE
Poniamo:
x = log a b
ax = b
Allora avremo:
Eleviamo ad n entrambi i membri:
(a )
x n
= bn
→
a n⋅ x = b n
log a b n = n ⋅ x = n ⋅ loga b
Mettendo in forma logaritmica avremo:
QED
………………………………………………………………………………………………………………
7a PROPRIETÀ DEI LOGARITMI
n
loga
LOGARITMO DI UNA RADICE
1
b = ⋅ loga b
n
Il logaritmo di una radice è uguale all’inverso dell’indice della radice moltiplicato per il logaritmo
DIMOSTRAZIONE
Poniamo:
x = log a b
ax = b
Allora avremo:
1
Eleviamo a entrambi i membri:
n
( )
1
x n
a
=
1
n
b
→
log a n b =
Mettendo in forma logaritmica avremo:
1
⋅x
n
a
=nb
1
1
⋅ x = ⋅ log a b
n
n
QED
………………………………………………………………………………………………………………
8a PROPRIETÀ DEI LOGARITMI
cambiamento di base
loga c
logb c =
loga b
DIMOSTRAZIONE
Poniamo:
Quindi:
x = log b c
e
( )
a xy = a y
x
in forma logaritmica: xy = log a c
y = log a b
= bx = c
→
bx = c
Allora avremo:
ossia
log b c ⋅ log a b = log a c
e
ay =b
a xy = c
→
log b c =
log a c
log a b
QED
………………………………………………………………………………………………………………
I logaritmi parte seconda – pag. 2 di 2
QUADRO RIASSUNTIVO PROPRIETÀ DEI LOGARITMI
loga 1 = 0
loga a = 1
loga a n = n
………………………………………………………………………………………………………………
loga bc = loga b + loga c
PRODOTTO
b
loga = loga b − loga c
c
RAPPORTO
………………………………………………………………………………………………………………
loga bn = n ⋅ loga b
loga
n
POTENZA DI ESPONENTE n
1
b = ⋅ loga b
n
RADICE DI INDICE n
………………………………………………………………………………………………………………
loga c
logb c =
loga b
CAMBIAMENTO DI BASE
EQUAZIONI LOGARITMICHE
Le equazioni logaritmiche sono equazioni in cui l’incognita x si trova nell’argomento (o nella base) di
uno o più logaritmi. Un primo metodo per risolvere un’equazione logaritmica è quello di cercare di
ricondurla alla forma:
loga f ( x ) = loga g ( x )
•
In questa forma le espressioni ad esponente f ( x ) e g ( x ) sono espressioni algebriche in x
(polinomi, frazioni, numeri…)
•
Notare che in questa equazione la base del logaritmo è la stessa in entrambi i membri
dell’equazione; dato che i logaritmi hanno lo stesso valore ed hanno uguale base devono avere
anche uguale argomento. L’equazione si risolverà quindi uguagliando gli esponenti
loga f ( x ) = loga g ( x )
•
•
f (x ) = g (x )
L’equazione così ottenuta è algebrica e quindi si risolve con i metodi già noti. Per ottenere un
unico logaritmo sia a sinistra che a destra dell’uguale si utilizzano in modo opportuno le proprietà
dei logaritmi.
Le soluzioni ottenute vanno poi controllate. Se una di esse rende negativo l’argomento o la base di
almeno uno dei logaritmi nel testo iniziale allora tale soluzione non è accettabile.
NB: Da qui in poi il termine log senza esprimere la base indica il logaritmo in base 10: log ⇔ log10
………………………………………………………………………………………………………………..
esempio 1
log(3 x − 1) + log(3 x + 6 ) = log(9 x + 2 )
applicando la proprietà del prodotto l’equazione diventa: log(3x − 1)(3x + 6) = log(9 x + 2 )
ora possiamo uguagliare gli argomenti :
quindi:
9 x 2 + 18 x − 3x − 6 = 9 x + 2
con la formula ridotta:
x1,2
(3x − 1)(3x + 6) = (9 x + 2)
→
9x 2 + 6x − 8 = 0
4
− 3 ± 9 + 72 − 3 ± 9
3
=
=
=
2
9
9
x2 = +
3
x1 = −
Controllo delle soluzioni
4
inserita nel primo logaritmo del testo fornisce log(− 5) con argomento negativo, quindi
3
non è accettabile come soluzione.
2
2. x = inserita nei tre logaritmi del testo fornisce tutti argomenti positivi, quindi è accettabile.
3
2
Cè quindi una sola soluzione: x =
3
………………………………………………………………………………………………………………..
Equazioni logaritmiche pag. 1
1. x = −
esempio 2
(
)
log x 2 − 6 x + 10 − log(26 − 13 x ) = log(4 − x ) − log 12
Conviene spostare da parte opposta dell’uguale i logaritmi con segno meno davanti, in modo da averli poi
col segno più e poter applicare la proprietà del prodotto:
(
)
log x 2 − 6 x + 10 + log 12 = log(4 − x ) + log(26 − 13x )
(
)
applicando la proprietà del prodotto l’equazione diventa: log x 2 − 6 x + 10 ⋅ 12 = log(4 − x )(26 − 13x )
(x
ora possiamo uguagliare gli argomenti :
)
− 6 x + 10 ⋅ 12 = (4 − x )(26 − 13x )
2
quindi: 12 x 2 − 72 x + 120 = 104 − 52 x − 26 x + 13x 2
con la formula ridotta
x1,2
− x 2 + 6 x + 16 = 0
→
→
x 2 − 6 x − 16 = 0
x1 = − 2
3 ± 9 + 16
=
=3±5=
1
x 2 = +8
Controllo delle soluzioni
1. x = −2 inserita nei logaritmi del testo fornisce tutti gli argomenti positivi, quindi è accettabile.
2. x = +8 inserita in log(4 − x ) fornisce log(− 4 ) con argomento negativo, quindi non è accettabile.
C’è una sola soluzione:
x = −2
………………………………………………………………………………………………………………..
esempio 3
(
)
log 5 − 8 x 2 + 22 x − log 5 (− 2 x + 6 ) = log 5 (− 4 x + 15)
Conviene spostare da parte opposta dell’uguale i logaritmi con segno meno davanti, in modo da averli poi
col segno più e poter applicare la proprietà del prodotto:
log 5 − 8 x 2 + 22 x = log 5 (− 4 x + 15) + log 5 (− 2 x + 6)
(
)
(
)
applicando la proprietà del prodotto l’equazione diventa: log 5 − 8 x 2 + 22 x = log 5 (− 4 x + 15)(− 2 x + 6)
ora possiamo uguagliare gli argomenti :
quindi: − 8 x 2 + 22 x = 8 x 2 − 24 x − 30 x + 90
con la formula ridotta
x1,2
(− 8x
2
→
)
+ 22 x = (− 4 x + 15)(− 2 x + 6)
− 16 x 2 + 76 x − 90 = 0
→
8 x 2 − 38 x + 45 = 0
9
19 ± 361 − 360 19 ± 1
4
=
=
=
5
8
8
x2 =
2
x1 =
Controllo delle soluzioni
9
inserita nei tre logaritmi del testo fornisce tutti gli argomenti positivi, quindi è accettabile.
4
5
2. x = inserita nei tre logaritmi del testo fornisce tutti gli argomenti positivi, quindi è accettabile.
2
1. x =
5
9
e x=
4
2
………………………………………………………………………………………………………………..
Ci sono quindi due soluzioni:
x=
Equazioni logaritmiche pag. 2
esempio 4
2 log(12 x − 5) − log(4 x − 1) = log(8 x − 3)
Conviene spostare da parte opposta dell’uguale i logaritmi con segno meno davanti, in modo da averli poi
col segno più e poter applicare la proprietà del prodotto:
2 log(12 x − 5) = log(8 x − 3) + log(4 x − 1)
applicando a sinistra la proprietà dell’esponente e a destra la proprietà del prodotto l’equazione diventa:
log(12 x − 5)2 = log(8 x − 3)(4 x − 1)
ora possiamo uguagliare gli argomenti :
(12 x − 5)2 = (8 x − 3)(4 x − 1)
quindi:
144 x 2 − 120 x + 25 = 32 x 2 − 8 x − 12 x + 3
→
con la formula ridotta
x1,2 =
112 x 2 − 100 x + 22 = 0
25 ± 625 − 616 25 ± 3
=
=
56
56
→
56 x 2 − 50 x + 11 = 0
11
28
1
x2 =
2
x1 =
Controllo delle soluzioni
1. x =
1
inserita nei logaritmi del testo fornisce tutti gli argomenti uguali a 1, quindi è accettabile.
2
11
2
inserita in log(12 x − 5) fornisce log − con argomento negativo, quindi non è
28
7
accettabile.
2. x =
C’è una sola soluzione:
x=
1
2
………………………………………………………………………………………………………………..
ESERCIZI PER LO STUDENTE DILIGENTE
Con gli stessi metodi degli esempi 1 – 2 – 3 - 4 risolvere gli esercizi del libro di testo a pag. 78
numeri 205 – 206 – 210 – 208.
………………………………………………………………………………………………………………..
ULTERIORI ESERCIZI:
pag. 78 numeri 207 – 212
………………………………………………………………………………………………………………..
Equazioni logaritmiche pag. 3
ALTRI TIPI DI EQUAZIONI LOGARITMICHE
Le equazioni logaritmiche sono poi risolvibili, a seconda dei casi, con diversi altri metodi. Vediamo
alcuni esempi che si possono presentare.
Esercizio 209 pag. 78
(
)
log 2 x 2 − 6 x + 9 = log 2 x − 2
(
→
)
log 2 x 2 − 6 x + 9 + 2 = log 2 x
il numero 2 va trasformato
anch’esso in logaritmo, come fare?
Utilizzando la proprietà: log a a n = n possiamo trasformarlo così: 2 = log 2 2 2 ottenendo:
(
)
(
→
log 2 x 2 − 6 x + 9 + log 2 2 2 = log 2 x
)
log 2 x 2 − 6 x + 9 + log 2 4 = log 2 x
(
)
applicando la proprietà del prodotto l’equazione diventa: log 2 x 2 − 6 x + 9 ⋅ 4 = log 2 x
(x
ora possiamo uguagliare gli argomenti :
2
4 x − 24 x + 36 = x
quindi:
2
)
− 6x + 9 ⋅ 4 = x
2
→
4 x − 25 x + 36 = 0
x1,2
9
x1 =
25 ± 625 − 576 25 ± 7
2
=
=
=
8
8
x2 = 4
Controllo delle soluzioni
1. x =
9
inserita nei logaritmi del testo fornisce tutti argomenti positivi, quindi è accettabile.
2
2. x = 4 inserita nei logaritmi del testo fornisce tutti argomenti positivi, quindi è accettabile.
9
e x=4
2
………………………………………………………………………………………………………………..
x=
Due soluzioni:
CAMBIAMENTO DI VARIABILE
esercizio 219 pag.79
log x
1
1
−
=
log x − 1 log 2 x + 2 log x − 3 log x + 3
→
y 2 + 3y − 1 = y − 1
→
y2 + 2y = 0
→
y 2 + 3y − 1
y −1
=
( y − 1)( y + 3) ( y − 1)( y + 3)
mcm
(*)
y
1
1
− 2
=
y −1 y + 2y − 3 y + 3
così facendo l’equazione diventa algebrica:
y
1
1
−
=
y − 1 ( y − 1)( y + 3) y + 3
conviene porre: y = log x
→
y( y + 2) = 0
equazione fratta
C.E.
y ≠1
y≠3
y = 0 e y = −2 accettabili
→
Ora dobbiamo tornare al cambiamento di variabile (*) per determinare i valori di x
1° caso:
y=0
2° caso:
y = −2
→
→
log x = 0
log x = −2
x = 10 0
→
→
→
x = 10 −2
x =1
→
x=
1
100
………………………………………………………………………………………………………………..
Altri tipi di equazioni logaritmiche pag. 1
CAMBIAMENTO DI BASE
es. 223 pag. 79
log 2 x + log 4 x + log 8 x = −11
Riduciamo i logaritmi nella stessa base. Siccome le tre basi sono potenze di 2, usiamo come base comune
proprio 2 e usiamo la formula del cambiamento di base dei logaritmi.
log 4 x =
log 2 x log 2 x
=
log 2 4
2
log 2 x +
log 2 x log 2 x
+
= 11
2
3
11 log 2 x = 66
→
e log 8 x =
log 2 x log 2 x
=
log 2 8
3
6 log 2 x + 3 log 2 x + 2 log 2 x 66
=
6
6
mcm
→
log 2 x = 6
→
quindi l’equazione diventa:
x = 26
→
x = 64
………………………………………………………………………………………………………………..
es. 225 pag. 79
log 3 (2 x − 3) − log 27 (2 x − 3) = 2
Trasformiamo in logaritmo a base 3:
log 27 (2 x − 3) =
log 3 (2 x − 3) log 3 (2 x − 3)
=
log 3 27
3
quindi l’equazione diventa:
log 3 (2 x − 3) −
log 3 (2 x − 3)
=2
3
2 log 3 (2 x − 3) = 6
→
mcm
→
log 3 (2 x − 3) = 3
3 log 3 (2 x − 3) − log 3 (2 x − 3) 6
=
3
3
→
2 x − 3 = 33
→
2 x − 3 = 27
→
x = 15
………………………………………………………………………………………………………………..
es. 230 pag. 79
log 2 x + 3 log 8
x=
3
2
1
3
log 2 x + 3 ⋅ log 8 x =
2
2
→
→
log 2 x +
3
3
log 8 x =
2
2
Riduciamo i logaritmi nella stessa base. Usiamo come base comune proprio 2 e usiamo la formula del
cambiamento di base dei logaritmi.
log 8 x =
log 2 x log 2 x
=
log 2 8
3
log 2 x +
log 2 x 3
=
2
2
log 2 x = 1
→
quindi l’equazione diventa: log 2 x +
mcm
→
x = 21
→
2 log 2 x + log 2 x 3
=
2
2
→
3 log 2 x 3
⋅
=
2
3
2
3 log 2 x = 3
x=2
………………………………………………………………………………………………………………..
Altri tipi di equazioni logaritmiche pag. 2










