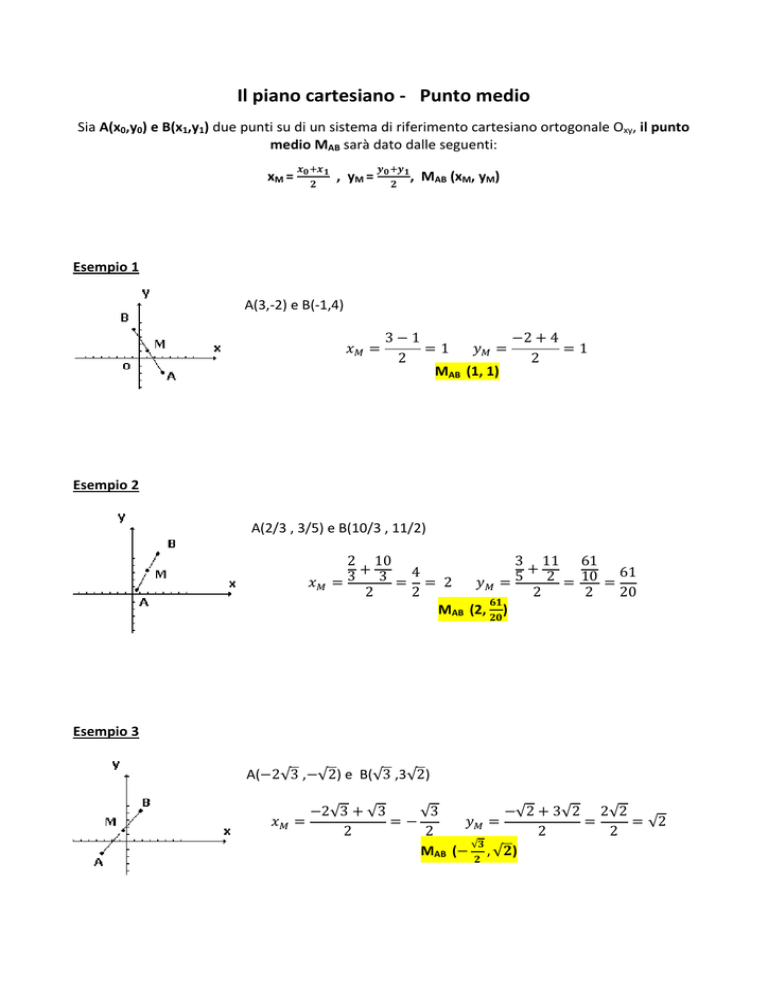
Il piano cartesiano ‐ Punto medio Sia A(x0,y0) e B(x1,y1) due punti su di un sistema di riferimento cartesiano ortogonale Oxy, il punto medio MAB sarà dato dalle seguenti: xM = , yM = , MAB (xM, yM) Esempio 1 A(3,‐2) e B(‐1,4) 3
1
2
2 4
2
1
MAB (1, 1) 1 Esempio 2 A(2/3 , 3/5) e B(10/3 , 11/2) 2
3
2
10
3
4
2
3
5
2
2
11
2
61
10
2
61
20
MAB (2, ) Esempio 3 A( 2√3 , √2) e B(√3 ,3√2) 2√3 √3
2
√3
2
MAB (
3√2
√2
√
2
, √ ) 2√2
2
√2 Problema Siano dati, su di un sistema di riferimento cartesiano ortogonale Oxy,i punti A(‐1,2), B(‐3,1), C(‐2,4). Dopo aver verificato che si ABC sia isoscele, verificare che l’altezza relativa alla base divide il triangolo ABC in due triangoli rettangoli. Per verificare che ABC sia un isoscele devo verificare che due lati sia isometrici. A(‐1,2), B(‐3,1), C(‐2,4) 1 2
AB
3 1
√4 1 √5 BC
2 3
4 1
√1 9 √10 4 2
AC
2 1
√1 4 √5 AB=AC Verificato che ABC sia Isoscele Sappiamo dalla geometria Euclidea che l’altezza relativa alla base di un triangolo isoscele coincide con la mediana AM con M punto medio di AB. Dunque , applicando la formula del punto medio si ha 3 2
5
1 4 5
2
2
2
2
H (
, ) Adesso bisogna verificare che i triangoli ABH e AHC siano rettangoli. Basta verificarlo per ABH e per questioni di simmetria lo sarà anche AHC. A(‐1,2), B(‐3,1), H ( , ) 2
AB =AH2+BH2 AB
√5 BH
AH
BC
5
2
√
, mentre AH bisogna calcolarlo 5
2
1
2
9
4
1
4
10
4
Sostituendo si ha √5
5
√10
√10
2
2
5 5
5
2 2
5 Verificato! √10
2